Signs of Trigonometric Functions
Understanding the signs of trigonometric functions is a key step in mastering trigonometry. Whether you're a high school student or preparing for competitive exams like JEE or NEET, knowing the sign of sin, cos, tan in all quadrants is essential for solving problems quickly and accurately. The quadrant signs of trigonometric functions change depending on the angle’s position in the coordinate plane, and this variation is summarized in the trigonometry signs table for all quadrants.
This Story also Contains
- What Are Trigonometric Functions and Why Do Their Signs Matter?
- Signs of Trigonometric Functions
- Variation in the Values of Trigonometric Functions in Different Quadrants
- Table of Signs of Trigonometric Functions
- Domain and Range of Trigonometric Functions
- Real-Life Applications of Trigonometric Sign Rules
- List of Topics Related to the Trigonometric Functions
- NCERT Resources
- Practice Questions on Signs of Trigonometric Functions
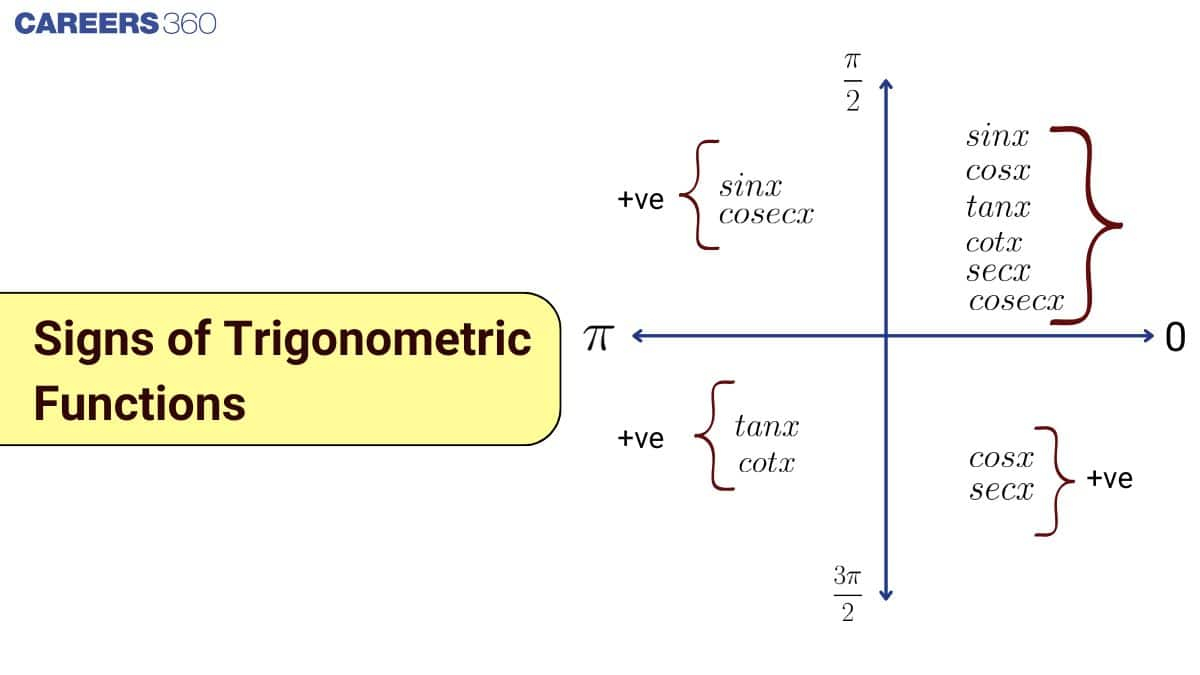
One effective way to remember this is through the ASTC rule in trigonometry, often recalled using the phrase "Add Sugar to Coffee". But what is the ASTC rule in trigonometry? It’s a memory trick that tells you which function is positive in each quadrant: All (I), Sine (II), Tangent (III), Cosine (IV). This article explains how to remember signs of trig functions, presents a clear table of signs of trigonometric functions, and includes a helpful sign chart of trig functions to make understanding the graphs of general trigonometric functions easier and more intuitive.
What Are Trigonometric Functions and Why Do Their Signs Matter?
In trigonometry, functions like sine, cosine, and tangent change their signs based on the quadrant of the angle. The signs of trigonometric functions are best understood using the ASTC rule in trigonometry, also remembered as "Add Sugar To Coffee". This rule explains in which quadrant sine is positive, and helps you know the sign of sin, cos, tan in all quadrants. A trigonometric function signs table or sign chart of trig functions makes it easy to recall these rules. Understanding the trigonometry signs table for all quadrants is essential for solving problems quickly in geometry, calculus, and physics.
Definition of Basic Trigonometric Functions (sin, cos, tan)
The three primary trigonometric functions are sine ($\sin$), cosine ($\cos$), and tangent ($\tan$). These functions are defined in terms of a right-angled triangle or using coordinates on the unit circle.
In a right-angled triangle:
- $\sin \theta = \dfrac{\text{Opposite side}}{\text{Hypotenuse}}$
- $\cos \theta = \dfrac{\text{Adjacent side}}{\text{Hypotenuse}}$
- $\tan \theta = \dfrac{\text{Opposite side}}{\text{Adjacent side}}$
When extended to the coordinate plane, if a point lies on the terminal side of angle $\theta$ at coordinates $(x, y)$ and the distance from the origin is $r = \sqrt{x^2 + y^2}$, then:
- $\sin \theta = \dfrac{y}{r}$
- $\cos \theta = \dfrac{x}{r}$
- $\tan \theta = \dfrac{y}{x}$
These formulas make it clear that the signs of $\sin$, $\cos$, and $\tan$ depend on whether $x$, $y$, and $r$ are positive or negative in a given quadrant.
Importance of Signs in Trigonometry
The signs of trigonometric functions in all quadrants are essential in solving problems involving angles greater than $90^\circ$ or negative angles. If you don’t understand which trig functions are positive in each quadrant, you may get the wrong values for angles or miss key steps in calculus, coordinate geometry, or physics.
For example, when solving an equation like:
$\cos \theta = -\dfrac{1}{2}$
You need to know that cosine is negative in the second and third quadrants, so:
$\theta = 120^\circ \text{ or } 240^\circ$
This is why competitive exams such as JEE, NEET, and CBSE Class 11 maths place strong emphasis on the signs of trig functions by quadrant.
Signs of Trigonometric Functions
The sign of trigonometric ratios of an angle depends on the quadrant in which the terminal side of the angle lies. We always take $OP = r$ as positive. Thus, the sign of trigonometric functions depends on the sign of $x and y$.

Assume $r = 1$, since this is a unit circle.
Let $P(a, b)$ be any point on the circle with angle $\angle AOP = x$ radians, i.e., the length of arc $AP = x$.
Clearly,
$\cos x = a$
$\sin x = b$
In the right triangle $OMP$ (with $O$ as the origin):
$OM^2 + MP^2 = OP^2$
$x^2 + y^2 = 1$
Thus, for every point on the unit circle:
$x^2 + y^2 = 1$
$\cos^2 x + \sin^2 x = 1$
Since one complete revolution subtends an angle of $2\pi$ radians at the center of the circle:
$\angle AOB = \dfrac{\pi}{2}$
$\angle AOC = \pi$
$\angle AOD = \dfrac{3\pi}{2}$
All angles which are integral multiples of $\dfrac{\pi}{2}$ are called quadrantal angles.
For these quadrantal angles, we have:
$\cos 0 = 1$
$\sin 0 = 0$
$\cos \dfrac{\pi}{2} = 0$
$\sin \dfrac{\pi}{2} = 1$
Now, if we take one complete revolution from point $P$, we return to the same point $P$ again.
Thus, we also observe that if $x$ increases or decreases by an integral multiple of $2\pi$, the values of sine and cosine functions remain unchanged:
$\sin(x + 2\pi) = \sin x$
$\cos(x + 2\pi) = \cos x$
Variation in the Values of Trigonometric Functions in Different Quadrants
Understanding how trigonometric functions behave in different quadrants of the coordinate plane is crucial for solving a wide range of trigonometry problems involving angles beyond $90^\circ$. As the angle $x$ increases from $0$ to $2\pi$, the values and signs of sine, cosine, tangent, and their reciprocals change depending on the quadrant. Below is a quadrant-wise analysis of this variation, along with the commonly used mnemonic rule "Add Sugar To Coffee" (ASTC).
First Quadrant: $0 < x < \dfrac{\pi}{2}$
Which trignometric ratios is positive in first quadrant? In the first quadrant $\sin \theta, \cos \theta, \tan \theta, \sec \theta, cosec \theta$, and $\cot \theta$ are all positive.
As $x$ increases from $0$ to $\dfrac{\pi}{2}$:
- $\sin x$ increases from $0$ to $1$
- $\cos x$ decreases from $1$ to $0$
- $\tan x$ increases from $0$ to $\infty$
- $\cot x$ decreases from $\infty$ to $0$
- $\sec x$ increases from $1$ to $\infty$
- $cosec x$ decreases from $\infty$ to $1$
Since both $x > 0$ and $y > 0$ in this quadrant, all trigonometric functions are positive.
Second Quadrant: $\dfrac{\pi}{2} < x < \pi$
As $x$ increases from $\dfrac{\pi}{2}$ to $\pi$:
- $\sin x$ decreases from $1$ to $0$
- $\cos x$ decreases from $0$ to $-1$
- $\tan x$ decreases from $\infty$ to $0$ (and is undefined at $\dfrac{\pi}{2}$)
- $\cot x$ increases from $0$ to $-\infty$
- $\sec x$ decreases from $\infty$ to $-1$
- $cosec x$ increases from $1$ to $\infty$
In this quadrant, $x < 0$ and $y > 0$, so only $\sin \theta$ and $cosec \theta$ are positive.
Third Quadrant: $\pi < x < \dfrac{3\pi}{2}$
Here, both $x < 0$ and $y < 0$. So:
- $\sin x < 0$
- $\cos x < 0$
- $\tan x > 0$
- $\cot x > 0$
- $\sec x < 0$
- $cosec x < 0$
Thus, only $\tan \theta$ and $\cot \theta$ are positive in the third quadrant.
Fourth Quadrant: $\dfrac{3\pi}{2} < x < 2\pi$
In this quadrant:
- $x > 0$ and $y < 0$
- $\cos x > 0$
- $\sec x > 0$
- All other trigonometric functions are negative
So, only $\cos \theta$ and $\sec \theta$ are positive here.

![]()
Quadrant-Wise Positivity of Trigonometric Functions
- First Quadrant: All six functions are positive
$\sin \theta > 0,\ \cos \theta > 0,\ \tan \theta > 0,\ cosec \theta > 0,\ \sec \theta > 0,\ \cot \theta > 0$ - Second Quadrant: Only sine and cosecant are positive
$\sin \theta > 0,\ cosec \theta > 0$ - Third Quadrant: Only tangent and cotangent are positive
$\tan \theta > 0,\ \cot \theta > 0$ - Fourth Quadrant: Only cosine and secant are positive
$\cos \theta > 0,\ \sec \theta > 0$
How do we decide the sign of the trigonometric ratios? The sign of trigonometric ratios of an angle depends on the quadrant in which the terminal side of the angle lies.
Mnemonic: Add Sugar To Coffee (ASTC Rule)
To easily remember which trigonometric functions are positive (when rotated counter clockwise) in which quadrant, use the mnemonic:
- A (Add) – All functions positive in Quadrant I
- S (Sugar) – Only Sine and Cosecant are positive in Quadrant II
- T (To) – Only Tangent and Cotangent are positive in Quadrant III
- C (Coffee) – Only Cosine and Secant are positive in Quadrant IV
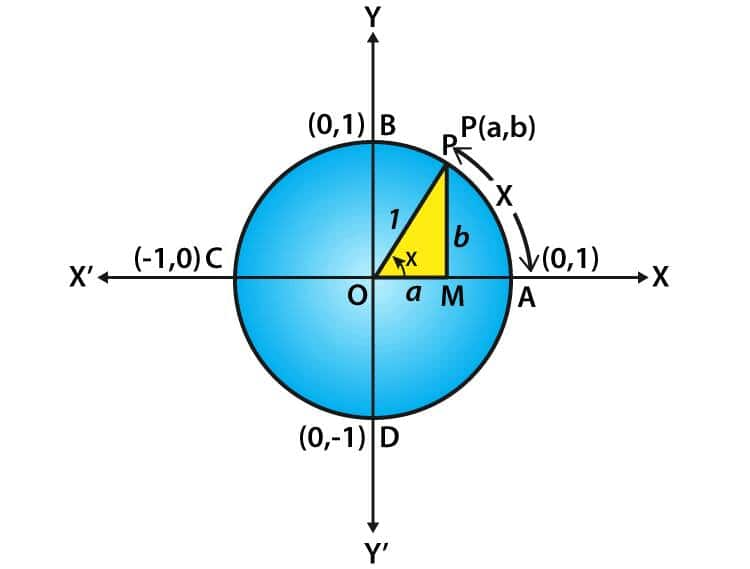
Depending on the signs of $x$ and $y$, the various trigonometric ratios will have different signs.
Table of Signs of Trigonometric Functions
The Table of Signs of Trigonometric Functions helps you quickly determine whether sine, cosine, tangent, and their reciprocals are positive or negative in each quadrant. Using the ASTC rule ("Add Sugar To Coffee"), this chart simplifies how to remember the signs of trig functions and is essential for solving trigonometry problems accurately.
| Quadrant | Sine ($\sin$) | Cosine ($\cos$) | Tangent ($\tan$) | Cosecant ($\csc$) | Secant ($\sec$) | Cotangent ($\cot$) |
|---|---|---|---|---|---|---|
| I (0° to 90°) | + | + | + | + | + | + |
| II (90° to 180°) | + | – | – | + | – | – |
| III (180° to 270°) | – | – | + | – | – | + |
| IV (270° to 360°) | – | + | – | – | + | – |
Domain and Range of Trigonometric Functions
Understanding the domain and range of trigonometric functions is essential for solving equations and evaluating expressions involving $\sin x$, $\cos x$, $\tan x$, and their reciprocals. These definitions come from how the functions behave on the unit circle and their algebraic relationships.
Domain of Trigonometric Functions
We observe that the point $P(a, b)$ on the unit circle can be obtained by rotating the terminal ray $OP$ any number of times—clockwise or anticlockwise. Therefore, the functions $\sin x$ and $\cos x$ are defined for all real values of $x$.
So, Domain of $\sin x$ and $\cos x$: $\mathbb{R}$
However, the function $\tan x$ is undefined where $\cos x = 0$ because:
$\tan x = \dfrac{\sin x}{\cos x}$
$\cos x = 0$ at $x = \dfrac{(2n+1)\pi}{2}$, where $n \in \mathbb{Z}$
So, Domain of $\tan x$ and $\sec x$:
$\mathbb{R} - \left\{ \dfrac{(2n+1)\pi}{2} \mid n \in \mathbb{Z} \right\}$
Similarly, $\cot x$ and $cosec x$ are undefined when $\sin x = 0$ because:
$\cot x = \dfrac{\cos x}{\sin x}$, and $cosec x = \dfrac{1}{\sin x}$
$\sin x = 0$ at $x = n\pi$, where $n \in \mathbb{Z}$
So, Domain of $\cot x$ and $cosec x$:
$\mathbb{R} - \left\{ n\pi \mid n \in \mathbb{Z} \right\}$
Range of Trigonometric Functions
Since the point $P(a, b)$ lies on the unit circle, the values of $a$ and $b$ are limited:
- $-1 \leq \cos x \leq 1$
- $-1 \leq \sin x \leq 1$
Thus, Range of $\sin x$ and $\cos x$:
$[-1, 1]$
The other functions are unbounded (except at points of discontinuity), so their ranges are:
- Range of $\tan x$ and $\cot x$:
$\mathbb{R}$ - Range of $\sec x$ and $cosec x$:
$(-\infty, -1] \cup [1, \infty)$
Domain and Range Table of Trigonometric Functions
Here’s a clear reference table for all six standard trigonometric ratios, it also helps in understanding the table of signs of trigonometric functions:
Trigonometric Function | Domain | Range |
$\sin x$ | $\mathbb{R}$ | $[-1, 1]$ |
$\cos x$ | $\mathbb{R}$ | $[-1, 1]$ |
$\tan x$ | $\mathbb{R} - \left\{ \dfrac{(2n+1)\pi}{2} \mid n \in \mathbb{Z} \right\}$ | $\mathbb{R}$ |
$\cot x$ | $\mathbb{R} - \left\{ n\pi \mid n \in \mathbb{Z} \right\}$ | $\mathbb{R}$ |
$\sec x$ | $\mathbb{R} - \left\{ \dfrac{(2n+1)\pi}{2} \mid n \in \mathbb{Z} \right\}$ | $(-\infty, -1] \cup [1, \infty)$ |
$cosec x$ | $\mathbb{R} - \left\{ n\pi \mid n \in \mathbb{Z} \right\}$ | $(-\infty, -1] \cup [1, \infty)$ |
Real-Life Applications of Trigonometric Sign Rules
Understanding positive and negative trig functions is not just important in exams, it has real-world uses too. For instance:
- In navigation and GPS, directions and angles are calculated using trigonometric functions signs to determine north-south or east-west components.
- In engineering, the behavior of rotating objects is modeled using sine and cosine functions, with their signs indicating direction of rotation.
- In physics, especially in projectile motion or oscillation problems, applying the correct sign to $\sin \theta$ or $\cos \theta$ ensures accurate modeling.
So whether you're calculating trig function signs in each quadrant or applying the ASTC rule in trigonometry, these sign rules have strong value both in theory and in real-life problem solving.
Solved Examples Based on Sign of Trigonometric Functions
Solution: Given: $4 \sec A + 5 = 0$
$\Rightarrow \sec A = -\dfrac{5}{4}$
Since $ABCD$ is a convex quadrilateral, angle $A$ lies between $\dfrac{\pi}{2}$ and $\pi$ (i.e., second quadrant), where:
$\cos A < 0$
$\sin A > 0$
$\tan A < 0$
Now, $\sec A = \dfrac{1}{\cos A} = -\dfrac{5}{4}$
$\Rightarrow \cos A = -\dfrac{4}{5}$
Using identity: $\sin^2 A + \cos^2 A = 1$
$\Rightarrow \sin^2 A = 1 - \left(-\dfrac{4}{5}\right)^2 = 1 - \dfrac{16}{25} = \dfrac{9}{25}$
$\Rightarrow \sin A = \dfrac{3}{5}$ (positive in second quadrant)
Now, $\tan A = \dfrac{\sin A}{\cos A} = \dfrac{\dfrac{3}{5}}{-\dfrac{4}{5}} = -\dfrac{3}{4}$
$cosec A = \dfrac{1}{\sin A} = \dfrac{5}{3}$
Now, let the quadratic equation with roots $\tan A$ and $cosec A$ be:
$(x - \tan A)(x - cosec A) = 0$
Substitute values: $\left(x + \dfrac{3}{4}\right)\left(x - \dfrac{5}{3}\right) = 0$
Multiply: $x^2 - \dfrac{5}{3}x + \dfrac{3}{4}x - \dfrac{15}{12} = 0$
Combine terms: $x^2 - \left(\dfrac{5}{3} - \dfrac{3}{4}\right)x - \dfrac{15}{12} = 0$
$\Rightarrow x^2 - \dfrac{11}{12}x - \dfrac{15}{12} = 0$
Multiply throughout by 12 to remove denominators:
$12x^2 - 11x - 15 = 0$
Example 2: Find the range of function $f(x) = \dfrac{1}{2 \sin x - 3}$.
Solution: We know that $-1 \leq \sin x \leq 1$
Multiplying the entire inequality by $2$:
$-2 \leq 2 \sin x \leq 2$
Subtracting $3$ from all parts: $-5 \leq 2 \sin x - 3 \leq -1$
So, the denominator $2 \sin x - 3$ lies in the interval $[-5, -1]$
Therefore, $f(x) = \dfrac{1}{2 \sin x - 3} \in \left( \dfrac{1}{-1}, \dfrac{1}{-5} \right) = (-1, -\dfrac{1}{5})$
Hence, the range of $f(x)$ is: ${(-1,\ -\dfrac{1}{5})$
Solution: We start with:
$\sqrt{cosec^2 \alpha + 2 \cot \alpha}$
Using the identity $cosec^2 \alpha = 1 + \cot^2 \alpha$, we get:
$= \sqrt{1 + \cot^2 \alpha + 2 \cot \alpha}$
This simplifies to:
$= \sqrt{(\cot \alpha + 1)^2}$
Which gives: $= |1 + \cot \alpha|$
Now, since $\dfrac{3\pi}{4} < \alpha < \pi$, $\alpha$ lies in the second quadrant.
In the second quadrant:
$\cot \alpha < 0 \Rightarrow 1 + \cot \alpha < 1$
So: $|1 + \cot \alpha| = -(1 + \cot \alpha)$
Therefore, the final answer is:
$-1 - \cot \alpha$
Solution: We start with: $\sqrt{3 - \sqrt{\dfrac{1}{1 + \cot^2 x}}}$
Using the identity $1 + \cot^2 x = cosec^2 x$, we get:
$= \sqrt{3 - \sqrt{\dfrac{1}{cosec^2 x}}}$
Now, since $\dfrac{1}{cosec^2 x} = \sin^2 x$, we get:
$= \sqrt{3 - |\sin x|}$
Since $x$ lies in the third quadrant, $\sin x < 0$, so:
$|\sin x| = -\sin x$
Therefore: $= \sqrt{3 + \sin x}$
Example 5: Find the value of the trigonometric function $cosec(-1350^\circ)$.
Solution: We know that trigonometric functions are periodic, and for $cosec x$, the period is $360^\circ$. So:
$cosec(-1350^\circ) = cosec(-1350^\circ + 4 \times 360^\circ)$
Now: $= cosec(-1350^\circ + 1440^\circ)$
$= cosec(90^\circ)$
Using standard values:
$cosec(90^\circ) = 1$
List of Topics Related to the Trigonometric Functions
To truly master trigonometric identities and their applications, students must first gain clarity on the foundational topics that support them. This section outlines all key concepts related to trigonometric functions—ranging from basic ratios and quadrant sign rules to advanced identities, transformations, and real-world applications.
NCERT Resources
To score well in Class 11 Maths and build a strong base for competitive exams, mastering NCERT Chapter 3 – Trigonometric Functions is crucial. This section provides all essential NCERT study materials, including detailed notes, solved exercises, and exemplar problems. These CBSE-aligned resources help clarify core trigonometric concepts like identities, formulas, and ratios through structured explanations and accurate solutions.
NCERT Class 11 Chapter 3 Trigonometric Functions Notes
Practice Questions on Signs of Trigonometric Functions
Consistent problem-solving is essential to fully understand the signs of trigonometric functions in different quadrants. This section features a curated collection of practice questions covering the signs of sine, cosine, tangent, and other trigonometric ratios. Designed for Class 11 students and competitive exam aspirants, these questions range from fundamental to advanced levels, understanding both conceptual clarity and exam readiness.
Sign Of Trigonometric Functions - Practice Question MCQ
We have provided the list of practice questions based on the next topics below:
Frequently Asked Questions (FAQs)
In the first quadrant sinθ,cosθ,tanθ,secθ,cscθ, and cotθ are all positive.
The range of each sinx and cosx is [−1,1].
In the third quadrant, so only tanθ and cotθ are positive, sinθ,cosθ,secθ, and cscθ are negative.
In the first Quadrant and second quadrant sin is positive. In the third quadrant and fourth quadrant, sin is negative.
The sign of trigonometric ratios of an angle depends on the quadrant in which the terminal side of the angle lies