Length of Tangent, Subtangent, Normal and Subnormal of Parabola

Parabola is a locus of points in a plane that are equidistant from both the directrix and the focus. This concept length of tangent, normal, sub-tangent and sub-normal of an parabola is used to determine important properties of the parabola.

In this article, we discuss about the length of the tangent, normal, sub-tangent and sub-normal of parabolas which falls under the topic of two dimensional Analytical Geometry. It is an important topic for not only board exam but also for the competitive exams.

Parabola

Parabola is a locus of points in a plane that are equidistant from both the directrix and the focus. The standard form of the equation of ellipse with centre $(0,0)$ is $y^2 = 4ax$.

When the vertex is $(h, k)$ and the axis of symmetry is parallel to $x$-axis, the equation of the parabola is either $(y-k)^2=4 a(x-h)$ or $(y-k)^2=-4 a(x-h)$

When the vertex is $(h, k)$ and the axis of symmetry is parallel to $y$-axis, the equation of the parabola is either $(x-h)^2=4 a(y-k)$ or $(x-h)^2=-4 a(y-k)$

Tangent of Parabola

A tangent is a straight line that touches the parabola at a single point without crossing it at that point. The equation of the tangent at a given point $\left(x_1, y_1\right)$ on the parabola is

$
y y_1=2 a\left(x+x_1\right)
$

Length of Tangent of Parabola

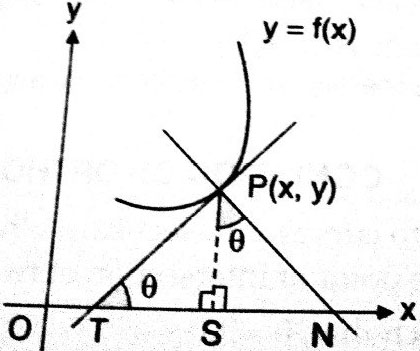
The length of the portion lying between the point of tangency i.e. the point on the curve from which a tangent is drawn and the point where the tangent meets the $x$-axis. Here point of tangency is $P\left(x_0, y_0\right)$

In the figure, the length of segment $PT$ is the length of the tangent.
In $\triangle PTS$

$
\begin{aligned}
\mathrm{PT} & =|y \cdot \csc \theta|=|y| \sqrt{1+\cot ^2 \theta} \\
& =|\mathrm{y}| \sqrt{1+\left(\frac{\mathrm{dx}}{\mathrm{dy}}\right)_{\left(\mathrm{x} 0, \mathrm{y}_0\right)}}
\end{aligned}
$

Length of Sub-Tangent of Parabola

The portion of the tangent along the $x$-axis from the point of contact of the tangent on the parabola to the intersection of the tangent at the $x$-axis is called the sub-Tangent.

The projection of the segment PT along the x-axis is the subtangent. In the figure, ST is the subtangent.
In $\triangle \mathrm{PST}$

$
\begin{aligned}
\mathrm{ST} & =|y \cdot \cot \theta|=\left|\frac{y}{\tan \theta}\right| \\
& =\left|\mathrm{y} \cdot \frac{\mathrm{dx}}{\mathrm{dy}}\right|
\end{aligned}
$

Normal of Parabola

Normal at a point of the ellipse is a line perpendicular to the tangent and passing through the point of contact. The equation of normal to the parabola $y^2=4 a x$ at point $P\left(x_1, y_1\right)$ is

$
\left(y-y_1\right)=\frac{-y_1}{2 a}\left(x-x_1\right)
$

Length of Normal of Parabola

A segment of normal $PN$ is the length of Normal.
In $\triangle \mathrm{PSN}$

$
\begin{aligned}
\mathrm{PN} & =\left|y \cdot \csc \left(90^{\circ}-\theta\right)\right|=|y \cdot \sec \theta| \\
& =|\mathrm{y}| \sqrt{1+\tan ^2 \theta}=|\mathrm{y}| \sqrt{1+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{\left(\mathrm{x} 0, \mathrm{y}_0\right)}}
\end{aligned}
$

Length of sub-Normal of Parabola

The portion of the normal along the $x$-axis from the point of contact of the tangent on the parabola to the intersection of the normal at the $x$-axis is called the sub-Normal.

The projection of the segment $PN$ along the $x$ -axis is the subnormal. In the figure, SN is the subnormal.
In $\triangle P S N$

$
\begin{aligned}
\mathrm{SN} & =\left|y \cdot \cot \left(90^{\circ}-\theta\right)\right|=|y \cdot \tan \theta| \\
& =\left|\mathrm{y} \cdot \frac{\mathrm{dy}}{\mathrm{dx}}\right|
\end{aligned}
$

Recommended Video Based on Length of Tangent, Sub-Tangent, Normal and Sub-Normal

Solved Examples Based on Length of Tangent, Sub-Tangent, Normal and Sub-Normal

Example 1:

The length of tangent drawn at $(4,4)$ on the curve $y^2=4 x$ is ?
1)$
3 \sqrt{5}
$

2)$
4 \sqrt{5}
$

3)$
5 \sqrt{5}
$

4)$
6 \sqrt{5}
$

Solution:

In $\triangle PTS$

$
\begin{aligned}
\mathrm{PT} & =|y \cdot \csc \theta|=|y| \sqrt{1+\cot ^2 \theta} \\
& =|\mathrm{y}| \sqrt{1+\left(\frac{\mathrm{dx}}{\mathrm{dy}}\right)_{\left(\mathrm{x} 0, \mathrm{y}_0\right)}}
\end{aligned}
$

Where $y^{\prime}=\frac{d y}{d x}$
length of tangent $=\frac{y}{y^1} \sqrt{1+\left(y^1\right)^2}$
$\because y^2=4 x \Rightarrow 2 y y^{\prime}=4 \Rightarrow y^{\prime}=2 / y \Rightarrow y^{\prime}$ at $(4,4)$ is $1 / 2$
$\therefore$ length $=\frac{4}{1 / 2} \sqrt{1+1 / 4}=4 \sqrt{5}$

Example 2: Length of normal to the curve $y=x^3$ at $(2,8)$ on it will be ?
1)$
8 \sqrt{45}
$

2)$
6 \sqrt{145}
$

3)$
7 \sqrt{145}
$

4)$
8 \sqrt{145}
$

Solution:

In $\triangle \mathrm{PSN}$

$
\begin{aligned}
\mathrm{PN} & =\left|y \cdot \csc \left(90^{\circ}-\theta\right)\right|=|y \cdot \sec \theta| \\
& =|\mathrm{y}| \sqrt{1+\tan ^2 \theta}=|\mathrm{y}| \sqrt{1+\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{(\mathrm{x} 0, \mathrm{y} 0)}}
\end{aligned}
$

Where $y^{\prime}=\frac{d y}{d x}$

$
d y / d x=3 x^2 \Rightarrow d y / d x \text { at }(2,8)=3^{\star} 2^2=12
$

$\therefore$ Length of normal $=8 \sqrt{1+144}=8 \sqrt{145}$

Example 3: Length of subtangent at any point on $y=e^x$ is equal to
1) $1$
2) $2$
3) $3$
4) $4$

Solution:

In $\triangle \mathrm{PST}$

$
\begin{aligned}
\mathrm{ST} & =|y \cdot \cot \theta|=\left|\frac{y}{\tan \theta}\right| \\
& =\left|\mathrm{y} \cdot \frac{\mathrm{dx}}{\mathrm{dy}}\right|
\end{aligned}
$

- wherein

Where $y^{\prime}=\frac{d y}{d x}$
Length of subtangent $=y / y^{\prime}=\frac{e^x}{e^x}=1$

Example 4: Length of subnormal drawn at $(2,4)$ on the curve $y^2=8 x$ equals
1) $4$
2) $2$
3) $3$
4) $5$

Solution:

In $\triangle \mathrm{PSN}$

$
\begin{aligned}
\mathrm{SN} & =\left|y \cdot \cot \left(90^{\circ}-\theta\right)\right|=|y \cdot \tan \theta| \\
& =\left|\mathrm{y} \cdot \frac{\mathrm{dy}}{\mathrm{dx}}\right|
\end{aligned}
$
Where $y^{\prime}=\frac{d y}{d x}$
Length of subnormal $=y y^{\prime} . . a t . .(2,4)$

$
y^2=8 x \Rightarrow 2 y y^{\prime}=8 \Rightarrow y^{\prime}=\frac{4}{y} \Rightarrow y^{\prime} . . a t . .(2,4)=1
$
Length of subnormal $=4$ x $1=4$

Example 5: For a curve $y=e^x$, at any point $\left(x_o, y_o\right)$ on it, the difference of the square of length of tangent and square of $y_o$ equals.
1) $1$
2) $2$
3) $3$
4) $4$

Solution:

Solution
As we know,
Length of tangent at $\left(\mathrm{x}_0, \mathrm{y}_0\right)$

$
\begin{aligned}
& y_o \sqrt{1+\frac{1}{\left(y^{\prime}\right)^2}} \\
& =\frac{y_o}{y^{\prime}} \sqrt{1+\left(y^{\prime}\right)^2} \\
& =\frac{e^{x_o}}{e^{x_o}} \sqrt{1+\left(e^{x_o}\right)^2}=\sqrt{1+\left(e^{x_o}\right)^2}=\sqrt{1+\left(y_o\right)^2}
\end{aligned}
$
Hence,

$
\Rightarrow(\text { length of tangent })^2-\left(y_0\right)^2=1
$
Hence, the answer is the option 1.

Summary

The lengths of the Tangent, Normal, sub-Tangent and sub-Normal of the parabola is used to determine the nature of the tangent and the curve respectively. This concept is used to determine the other properties of the parabola. In real life, this can be used to design satellites, parabolic arches for bridges and buildings etc.