Sum to Product Formula: List, Proof, Examples, Application

The Sum/Difference to Product formulas in trigonometry enable us to transform expressions involving the sum or difference of sine and cosine functions into products of sine and cosine functions. These formulas are applied to simplify trigonometric expressions by converting sums and differences into products. We use the sum-to-product formula to simplify and solve mathematical problems in trigonometry.

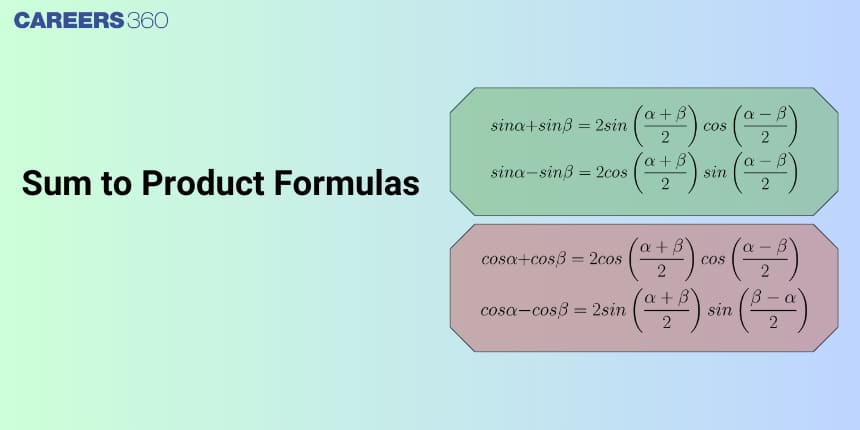
In this article, we will cover the concept of the sum-to-product formula in detail and derive these formulas using the product-to-sum formulas. This category falls under the broader category of trigonometry, which is a crucial Chapter in class 11 Mathematics. Additionally, we will examine practical applications through solved examples for a better understanding of the concept.

Sum/Difference into Product

The Sum/Difference formula is used to express the sum or difference of sine and cosine functions into the Product of sine and cosine functions.

Sum/Difference into Product formula

Sum/ Difference -to-Product formulas provide a powerful tool for simplifying trigonometric expressions involving the sum or difference of sines and cosines, and the sum/ difference to Product formulas are:

1. $\sin \alpha+\sin \beta=2 \sin \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)$
2. $\sin \alpha-\sin \beta=2 \sin \left(\frac{\alpha-\beta}{2}\right) \cos \left(\frac{\alpha+\beta}{2}\right)$
3. $\cos \alpha-\cos \beta=-2 \sin \left(\frac{\alpha+\beta}{2}\right) \sin \left(\frac{\alpha-\beta}{2}\right)$
4. $\cos \alpha+\cos \beta=2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)$

What are the Sum/ Difference to Product Formulas?

The Sum/ Difference formula is used to express the Sum/ Difference of sine and cosine functions into the product of sine and cosine functions. The sum and difference formulas of sine and cosine functions are added or subtracted to derive these identities. The Sum/ Difference to Product identities can be used to simplify the trigonometric expression.

where, $\alpha$ and $\beta$ are two angles of a triangle
1) $\sin \alpha+\sin \beta=2 \sin (\alpha+\beta) / 2 \cos (\alpha-\beta) / 2$

This formula converts the sum of the sine of two different angles into twice the product of the sine and the cosine of the angle.

where, $\alpha$ and $\beta$ are two angles of a triangle
1) $\sin \alpha+\sin \beta=2 \sin \left(\alpha^{+} \beta\right) / 2 \cos \left(\alpha^{-} \beta\right) / 2$

This formula converts the sum of the sine of two different angles into twice the product of the sine and the cosine of the angle.
2) $\sin \alpha-\sin \beta=2 \sin \left(\alpha_{-} \beta\right) / 2 \cos \left(\alpha^{+} \beta\right) / 2$

This formula converts the difference of the sine of two different angles into twice the product of the sine and cosine of the angle
3) $\cos \alpha-\cos \beta=-2 \sin (\alpha+\beta) / 2 \sin (\alpha-\beta) / 2$

This formula converts the difference of the cosine of two different angles into the negative of twice the product of the sine of an angle

Proof of Sum/ Difference to Product Formulas

These formulas can be derived from the product-to-sum identities. For example, with a few substitutions, we can derive the sum-to-product identity for sine.

Let : $\frac{u+v}{2}=\alpha$ and $\frac{u-v}{2}=\beta$
Then,

$
\begin{aligned}
\alpha+\beta & =\frac{u+v}{2}+\frac{u-v}{2} \\
& =\frac{2 u}{2} \\
& =u \\
\alpha-\beta & =\frac{u+v}{2}-\frac{u-v}{2} \\
& =\frac{2 v}{2} \\
& =v
\end{aligned}
$

Thus, by replacing $\alpha$ and $\beta$ in the product-to-sum formula with the substitute expressions, we have $\begin{aligned} 2 \sin \alpha \cos \beta & =\sin (\alpha+\beta)+\sin (\alpha-\beta) \\ 2 \sin \left(\frac{u+v}{2}\right) \cos \left(\frac{u-v}{2}\right) & =\sin u+\sin v, \quad \text { Substitute for }(\alpha+\beta) \text { and }(\alpha-\beta)\end{aligned}$

The other sum-to-product identities are derived similarly.|

Solved Examples Based on Sum/Difference into Product

Example 1: The value of $\cos 75^{\circ}+\cos 15^{\circ}$ is.
Solution
Given that,
$
\cos 75^{\circ}+\cos 15^{\circ}
$

Using the trigonometric formula,|

$
\cos x+\cos y=2 \cos \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right)
$

Therefore,

$
\begin{aligned}
& \cos 75^{\circ}+\cos 15^{\circ}=2 \cos \left(\frac{75^{\circ}+15^{\circ}}{2}\right) \cos \left(\frac{75^{\circ}-15^{\circ}}{2}\right) \\
& \cos 75^{\circ}+\cos 15^{\circ}=2 \cos \left(\frac{90^{\circ}}{2}\right) \cos \left(\frac{60^{\circ}}{2}\right) \\
& \cos 75^{\circ}+\cos 15^{\circ}=2 \cos \left(45^{\circ}\right) \cos \left(30^{\circ}\right) \\
& \cos 75^{\circ}+\cos 15^{\circ}=2\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right) \\
& \cos 75^{\circ}+\cos 15^{\circ}=\frac{\sqrt{3}}{\sqrt{2}}
\end{aligned}
$

Hence, the required answer is $\frac{\sqrt{3}}{\sqrt{2}}$

Example 2: If $0<x, y<\pi$ and

$
\cos x+\cos y-\cos (x+y)=\frac{3}{2}
$

then $\sin x+\cos y$ is equal to :

Solution: The given equation is

$
\cos x+\cos y-\cos (x+y)=\frac{3}{2}
$

You can think of
$
\frac{1}{2}+\frac{1}{2}-\left(-\frac{1}{2}\right)=\frac{3}{2}
$

for this to be true

$
x=y=60^{\circ}
$

So,

$
\sin 60^{\circ}+\cos 60^{\circ}=\frac{\sqrt{3}}{2}+\frac{1}{2}
$

OR

$
\begin{aligned}
& 2 \cos \left(\frac{x+y}{2}\right) \cos \left(\frac{x-y}{2}\right)-\left[2 \cos ^2\left(\frac{x+y}{2}\right)-1\right]=\frac{3}{2} \\
& 2 \cos \left(\frac{x+y}{2}\right)\left[\cos \left(\frac{x-y}{2}\right)-\cos \left(\frac{x+y}{2}\right)\right]=\frac{1}{2} \\
& 2 \cos \left(\frac{x+y}{2}\right)\left[2 \sin \left(\frac{x}{2}\right) \cdot \sin \left(\frac{y}{2}\right)\right]=\frac{1}{2} \\
& \cos \left(\frac{x+y}{2}\right) \cdot \sin \left(\frac{x}{2}\right) \cdot \sin \left(\frac{y}{2}\right)=\frac{1}{8} \\
& x=y=60^{\circ}
\end{aligned}
$
Hence, the required answer is

$
\frac{1+\sqrt{3}}{2}
$

Example 3: The value of
$
\cos (\alpha+\beta+\gamma)+\cos (\gamma+\alpha-\beta)+\cos (\alpha+\beta-\gamma)+\cos (\beta+\gamma-\alpha) \text { is }
$

Solution: The given expression can be rearranged as

$
\begin{aligned}
& \cos (\alpha+\beta+\gamma)+\cos (\alpha+\beta-\gamma)+\cos (\gamma+\alpha-\beta)+\cos (\beta+\gamma-\alpha) \\
& =2 \cos \gamma \cdot \cos (\alpha+\beta)+2 \cos \gamma \cos (\alpha-\beta) \\
& =2 \cos \gamma \cdot 2 \cos (\alpha) \cos (\beta) \\
& =4 \cos \gamma \cdot \cos (\alpha) \cos (\beta)
\end{aligned}
$
Hence, the required answer is $4 \cos \alpha \cdot \cos \beta \cdot \cos \gamma$
Example 4: The value of $\sin 75^{\circ}-\sin 15^{\circ}$ is.
Solution:
Given that,
Using the trigonometric formula,

$
\begin{aligned}
& \sin x-\sin y=2 \cos \left(\frac{x+y}{2}\right) \sin \left(\frac{x-y}{2}\right) \\
& \text { Therefore, } \\
& \sin 75^{\circ}-\sin 15^{\circ}=2 \cos \left(\frac{75^{\circ}+15^{\circ}}{2}\right) \sin \left(\frac{75^{\circ}-15^{\circ}}{2}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=2 \cos \left(\frac{90^{\circ}}{2}\right) \sin \left(\frac{60^{\circ}}{2}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=2 \cos \left(45^{\circ}\right) \sin \left(30^{\circ}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=2\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=\frac{1}{\sqrt{2}}
\end{aligned}
$

Given that,
Using the trigonometric formula, $\sin x-\sin y=2 \cos \left(\frac{x+y}{2}\right) \sin \left(\frac{x-y}{2}\right)$
Therefore,

$
\begin{aligned}
& \sin 75^{\circ}-\sin 15^{\circ}=2 \cos \left(\frac{75^{\circ}+15^{\circ}}{2}\right) \sin \left(\frac{75^{\circ}-15^{\circ}}{2}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=2 \cos \left(\frac{90^{\circ}}{2}\right) \sin \left(\frac{60^{\circ}}{2}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=2 \cos \left(45^{\circ}\right) \sin \left(30^{\circ}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=2\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right) \\
& \sin 75^{\circ}-\sin 15^{\circ}=\frac{1}{\sqrt{2}}
\end{aligned}
$

Hence, the required answer is $\frac{1}{\sqrt{2}}$

Example 5: Find the value of $\sin 55^{\circ}+\sin 65^{\circ}+\sqrt{3} \cos 175^{\circ}$
Solution

$
\begin{aligned}
& \sin 55^{\circ}+\sin 65^{\circ}+\sqrt{3} \cos 175^{\circ} \\
= & 2 \sin \left(\frac{55+65}{2}\right) \cos \left(\frac{55-65}{2}\right)+\sqrt{3} \cos 175^{\circ} \\
= & 2 \sin 60^{\circ} \cos \left(-5^{\circ}\right)+\sqrt{3} \cos (180-5)^{\circ} \\
= & 2 \frac{\sqrt{3}}{2} \cos \left(-5^{\circ}\right)+\sqrt{3} \cos (180-5)^{\circ} \\
= & \sqrt{3} \cos \left(-5^{\circ}\right)-\sqrt{3} \cos (5)^{\circ} \\
= & 0
\end{aligned}
$
Hence, the required answer is 0

Summary

The Sum to product formulas in trigonometry are used for simplifying and transforming sums of trigonometric functions into products. These formulas are essential in various applications, including simplifying complex trigonometric expressions, solving equations, and deriving identities. Understanding and applying these formulas enhances problem-solving skills in trigonometry.