Summation of Series in Trigonometry

Before delving into the trigonometric series, let's first understand what a is series. If we add or subtract all the terms of a sequence we will get an expression, which is called a series. It is denoted by S_n. Trigonometric series are expressions that involve the sum of trigonometric functions such as sine, cos, etc. It is a vital tool for mathematical analysis.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Trigonometric Series
2. Trigonometric Series Formula
3. Solved Example Based on Trigonometric Series

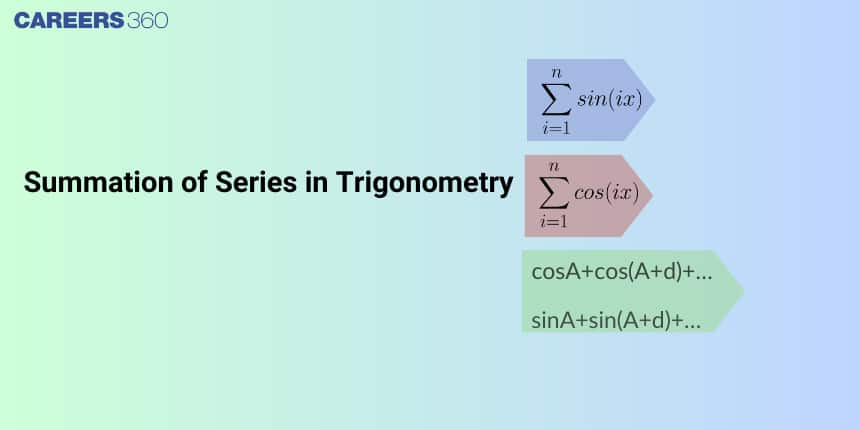
Trigonometric Series

In trigonometry, there are six basic trigonometric functions. These functions are trigonometric ratios that are based on ratios of sides in a right triangle: the hypotenuse (the longest side), the base (the side adjacent to a chosen angle), and the perpendicular (the side opposite the chosen angle). These functions are sine, cosine, tangent, secant, cosecant, and cotangent. They help us find different values in triangles by comparing these side lengths.

Trigonometric Functions Formulas

Using the sides of a right-angled triangle, we may use specific formulas to get the values of the trigonometric functions. We utilize the shortened form of these functions to write these formulas. The notation for sine is sin; the notation for cosine is cos; the notation for tangent is tan; the notation for secant is sec; the notation for cosecant is cosec; and the notation for cotangent is cot. The basic formulas to find the trigonometric functions are as follows:

$\sin \theta=$ Perpendicular/Hypotenuse
$\cos \theta=$ Base/Hypotenuse
$\tan \theta=$ Perpendicular/Base
$\sec \theta=$ Hypotenuse/Base
$\operatorname{cosec} \theta=$ Hypotenuse/Perpendicular
$\cot \theta=$ Base/Perpendicular

Trigonometric Series Formula

For sine series

$
\begin{gathered}
\sin (\alpha)+\sin (\alpha+\beta)+\sin (\alpha+2 \beta)+\sin (\alpha+3 \beta)+\ldots \ldots \ldots \ldots \ldots+\sin (\alpha+(n-1) \beta) \\
=\frac{\sin \left(\frac{\mathrm{n} \beta}{2}\right) \cdot \sin \left[\alpha+(\mathrm{n}-1) \frac{\beta}{2}\right]}{\sin \left(\frac{\beta}{2}\right)}
\end{gathered}
$

Proof:
Let $S=\sin \alpha+\sin (\alpha+\beta)+\sin (\alpha+2 \beta)+\cdots+\sin (\alpha+\overline{n-1} \beta)$
Here angle are in A.P. and common difference of angles $=\beta$ multiplying both side by $2 \sin \frac{\beta}{2}$ we get,

$
\begin{aligned}
& 2 S \sin \frac{\beta}{2}=2 \sin \alpha \sin \frac{\beta}{2}+2 \sin (\alpha+\beta) \sin \frac{\beta}{2}+\cdots+2 \sin (\alpha+\overline{n-1} \beta) \sin \frac{\beta}{2} \\
& \text { Now, } 2 \sin \alpha \sin \frac{\beta}{2}=\cos \left(\alpha-\frac{\beta}{2}\right)-\cos \left(\alpha+\frac{\beta}{2}\right) \\
& 2 \sin (\alpha+\beta) \sin \frac{\beta}{2}=\cos \left(\alpha+\frac{\beta}{2}\right)-\cos \left(\alpha+\frac{3 \beta}{2}\right) \\
& 2 \sin (\alpha+2 \beta) \sin \frac{\beta}{2}=\cos \left(\alpha+\frac{\beta \beta}{2}\right)-\cos \left(\alpha+\frac{5 \beta}{2}\right) \\
& \ldots \\
& \cdots \\
& \cdots \\
& 2 \sin (\alpha+\overline{n-1} \beta) \sin \frac{\beta}{2}=\cos \left[\alpha+(2 n-3) \frac{\beta}{2}\right]-\cos \left[\alpha(2 n-1) \frac{\beta}{2}\right]
\end{aligned}
$

Adding all the above we get

$
\begin{aligned}
& 2 \sin \frac{\beta}{2} \mathrm{~S}=\cos \left(\alpha-\frac{\beta}{2}\right)-\cos \left(\alpha+(2 \mathrm{n}-1) \frac{\beta}{2}\right) \\
& \text { or } \\
& 2 \sin \frac{\beta}{2} \mathrm{~S}=2 \sin \left(\alpha+(\mathrm{n}-1) \frac{\beta}{2}\right) \sin \frac{\mathrm{n} \beta}{2} \\
& \Rightarrow \mathrm{S}=\frac{\sin \left(\alpha+(\mathrm{n}-1) \frac{\beta}{2}\right) \sin \frac{\mathrm{n} \beta}{2}}{\sin \frac{\beta}{2}}
\end{aligned}
$

For cosine series

In the above result replacing ' $\alpha$ ' by ' $\pi / 2+\alpha$ ' we get

$
\cos \alpha+\cos (\alpha+\beta)+\cos (\alpha+2 \beta)+\cdots+\cos (\alpha+\overline{n-1} \beta)=\frac{\sin \frac{n \beta}{2}}{\sin \frac{\beta}{2}} \cos \left[\alpha+(n-1) \frac{\beta}{2}\right]
$

Recommended Video Based on Trigonometric Series

Solved Example Based on Trigonometric Series

Example 1: The value of $\sin \left(1^{\circ}\right)+\sin \left(3^{\circ}\right) \ldots+\sin \left(87^{\circ}\right)+\sin \left(89^{\circ}\right)$ is
1) $\frac{1}{\sin \left(1^{\circ}\right)}$
2) $\frac{1}{2 \sin \left(1^{\circ}\right)}$
3) $\frac{1}{2 \sin \left(2^{\circ}\right)}$
4) None of these

Solution

$
\sin \left(1^{\circ}\right)+\sin \left(3^{\circ}\right) \ldots+\sin \left(87^{\circ}\right)+\sin \left(89^{\circ}\right)
$

Here $a=1^{\circ}, b=2^{\circ}$ and $n=45$

$
\begin{aligned}
& \text { Sum }=\frac{\sin \left(a+(n-1) \frac{b}{2}\right) \sin \frac{n b}{2}}{\sin \frac{b}{2}} \\
& =\frac{\sin \left(1+44 * \frac{2}{2}\right) \sin \frac{45 * 2}{2}}{\sin \frac{2}{2}} \\
& =\frac{1}{2 \sin \left(1^{\circ}\right)}
\end{aligned}
$
Hence, the answer is option 2.

Example 2: The sum of $\cos \left(1^{\circ}\right)+\cos \left(3^{\circ}\right) \ldots+\cos \left(87^{\circ}\right)+\cos \left(89^{\circ}\right)$ is
1) $\frac{1}{2 \cos \left(1^{\circ}\right)}$
2) $\frac{1}{\sin \left(1^{\circ}\right)}$
3) $\frac{1}{2 \sin \left(1^{\circ}\right)}$
4) None of these

Solution

$
\cos \left(1^{\circ}\right)+\cos \left(3^{\circ}\right) \ldots+\cos \left(87^{\circ}\right)+\cos \left(89^{\circ}\right)
$
Here $a=1^{\circ}, b=2^{\circ}$ and $n=45$

$
\begin{aligned}
& \text { Sum }=\frac{\cos \left(a+(n-1) \frac{b}{2}\right) \sin \frac{n b}{2}}{\sin \frac{b}{2}} \\
& =\frac{\cos \left(1+44 * \frac{2}{2}\right) \sin \frac{45 * 2}{2}}{\sin \frac{2}{2}} \\
& =\frac{1}{2 \sin \left(1^{\circ}\right)}
\end{aligned}
$

Hence, the answer is option 3 .

Example 3: Let
$\mathrm{S}=\left\{\theta \in\left(0, \frac{\pi}{2}\right): \sum_{\mathrm{m}=1}^9 \sec \left(\theta+(\mathrm{m}-1) \frac{\pi}{6}\right) \sec \left(\theta+\frac{\mathrm{m} \pi}{6}\right)=-\frac{8}{\sqrt{3}}\right\}$. Then :
1) $\mathrm{S}=\left\{\frac{\pi}{12}\right\}$
2) $\mathrm{S}=\left\{\frac{2 \pi}{3}\right\}$
3) $\sum_{\theta \in S} \theta=\frac{\pi}{2}$
$\sum_{\text {4) }} \theta \in=\frac{3 \pi}{4}$
Solution
$\sec \left(\theta+\frac{m \pi}{6}-\frac{\pi}{6}\right) \cdot \sec \left(\theta+\frac{m \pi}{6}\right)$
$=\frac{1}{\sin \left(\frac{\pi}{6}\right)} \frac{\sin \left(\frac{\pi}{6}\right)}{\left[\cos \left(\theta+\frac{m \pi}{6}-\frac{\pi}{6}\right) \cos \left(\theta+m \frac{\pi}{6}\right)\right]}$
$=2\left[\frac{\sin \left[\left(\theta+\frac{m \pi}{6}\right)-\left(\theta+\frac{m \pi}{6}-\frac{\pi}{6}\right)\right]}{\cos \left(\theta+\frac{m \pi}{6}-\frac{\pi}{6}\right) \cos \left(\theta+\frac{m \pi}{6}\right)}\right]$
$=2\left[\tan \left(\theta+\frac{\mathrm{m} \pi}{6}\right)-\tan \left(\theta+\frac{\mathrm{m} \pi}{6}-\frac{\pi}{6}\right)\right]$
$\sum_{\mathrm{m}=1}^9 2\left[\tan \left(\theta+\frac{9 \pi}{6}\right)-\tan (\theta)\right]$
$\frac{-2}{\sin \theta \cos \theta}=\frac{-4}{\sin 2 \theta}$
$\frac{-4}{\sin 2 \theta}=-\frac{8}{\sqrt{3}}$
$\Rightarrow \sin 2 \theta=\frac{\sqrt{3}}{2}$
$\Rightarrow 2 \theta=60^{\circ}, 120^{\circ}$
$\Rightarrow \theta=30^{\circ}, 60^{\circ}$
$
S=\left\{\frac{\pi}{6}, \frac{\pi}{3}\right\}
$

Hence, the answer is the option 3 .

Example 4: The value of $\cos \frac{\pi}{19}+\cos \frac{3 \pi}{19}+\cos \frac{5 \pi}{19}+\ldots . .+\cos \frac{17 \pi}{19}$ is equal to (up to one decimal point):
1) $0.5$
2) $0$
3) $1$
4) $0.7$

Solution

The trigonometric ratios for angles in all the four quadrants.

$
\begin{aligned}
& \cos \frac{\pi}{19}+\cos \frac{3 \pi}{19}+\cos \frac{5 \pi}{19}+\ldots .+\cos \frac{17 \pi}{19} \\
& \text { Here, } A=\frac{\pi}{19}, D=\frac{2 \pi}{19}, n=9 \\
& \because \cos A+\cos (A+D)+\cos (A+2 D)+\ldots \ldots . .+\cos (A+(n-1) D) \\
& =\frac{\sin \left(\frac{n D}{2}\right)}{\sin \frac{D}{2}} \cdot \cos \left(\frac{2 A+(n-1) D}{2}\right)=\frac{\sin 9 \times \frac{\pi}{19}}{\sin \frac{\pi}{19}} \times \cos \left(\frac{\frac{\pi}{19}+\frac{17 \pi}{19}}{2}\right) \\
& =\frac{\sin \frac{9 \pi}{19}}{\sin \frac{\pi}{19}} \times \cos \frac{9 \pi}{19} \\
& =\frac{1}{2} \cdot \frac{\sin \left(\frac{18 \pi}{19}\right)}{\sin \frac{\pi}{19}}=\frac{1}{2} \cdot \frac{\sin \frac{\pi}{19}}{\sin \frac{\pi}{19}}=\frac{1}{2}
\end{aligned}
$

Example 5: The value of the sum $\sum_{k=1}^n\left(\tan 2^{k-1} \cdot \sec 2^k\right)$ is
1) $\tan 2^n$
2) $\tan 2^n-1$
3) $\tan 2^n-\tan 1$
4) $\cos 2^n-\cos 2$

Solution

$
\sum_{k=1}^n\left(\tan 2^{k-1} \cdot \sec 2^k\right)
$

$
\begin{aligned}
& \text { As } \sec \left(2.2^{k-1}\right)=\frac{1}{\cos \left(2.2^{k-1}\right)} \\
& =\sum_{k=1}^n \tan 2^{k-1} \times \frac{1+\tan ^2 2^{k-1}}{1-\tan ^2 2^{k-1}} \\
& =\sum_{k=1}^n\left(\frac{\tan (2)^{k-1}\left[2-1+\tan ^2 2^{k-1}\right]}{1-\tan ^2 2^{k-1}}\right) \\
& =\sum_{k=1}^n\left(\frac{2 \tan 2^{k-1}}{1-\tan ^2 2^{k-1}}-\tan (2)^{k-1}\right) \\
& =\sum_{k=1}^n\left(\tan 2^k-\tan 2^{k-1}\right) \\
& =\tan 2-\tan (1)+\tan 2^2-\tan 2+\ldots \tan 2^n-\tan 2^{n-1} \\
& =\tan 2^n-1
\end{aligned}
$

Hence, the answer is the option 3.