Trace of a matrix and properties

Edited By Komal Miglani | Updated on Jul 02, 2025 06:33 PM IST

Before we start with the concept of a trace of matrices, let’s first understand what is a matrix. A rectangular arrangement of objects (numbers or symbols or any other objects) is called a matrix (plural: matrices). A matrix is only a representation of the symbol, number, or object. It does not have any value. Usually, a matrix is denoted by capital letters. Matrix of order m × n, (read as m by n matrix) means that the matrix has m number of rows and n number of columns. In real life, we can use a trace of the matrix to construct Hamiltonians for quantum systems with discrete and finite sets of energy equivalence.

This Story also Contains

Square matrix
Trace of the matrix:
Properties of a trace of the matrix:
Solved Examples Based on Trace of Matrices

Trace of a matrix and properties

In this article, we will cover the concept trace of matrices. This category falls under the broader category of Matrices, which is a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of eight questions have been asked on this topic in Jee mains (2013 to 2023), one in 2013, one in 2021.

Square matrix

The square matrix is the matrix in which the number of rows $=$ number of columns. So a matrix $A=\left[a_{i j}\right]_{m \times n}$ is said to be a square matrix when $m=n$. E.g.
$\left[\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right]_{3 \times 3}$ or, $\left[\begin{array}{cc}2 & -4 \\ 7 & 3\end{array}\right]_{2 \times 2}$

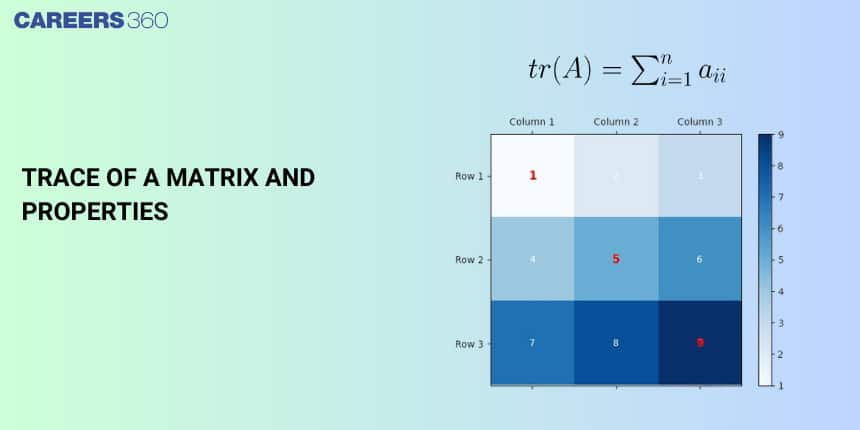
Trace of the matrix:

The sum of all diagonal elements of a square matrix is called the trace of a matrix. Lying along the principal diagonal is called the trace of A.

The trace of the matrix is denoted by Tr(A) or tr.A.

$
\operatorname{Tr}(\mathrm{A})=\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{a}_{\mathrm{ii}}
$

Let us consider the square matrix of order $3 \times 3$ as shown below. The elements of the matrix are $a_{11}, a_{12}, a_{13}$ $\qquad$ , $a_{33}$. The principal diagonal elements are $a_{11}, a_{22}, a_{33}$. So trace of the matrix is the sum of all principal diagonal elements.
$
\begin{aligned}
& A=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right] \\
& \operatorname{Tr}(A)=a_{11}+a_{22}+a_{33}
\end{aligned}
$

Eg.
For a given matrix $\mathrm{A}$,
$
A=\left[\begin{array}{ccc}
-2 & 4 & 7 \\
8 & 3 & -1 \\
5 & -6 & 9
\end{array}\right], \operatorname{Tr}(\mathrm{A})=-2+3+9=10
$

Properties of a trace of the matrix:

Given below are some properties of the trace of a matrix. Let us consider two square matrices A and B

$\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}} ; \mathrm{B}=\left[\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}}$ and $\mathrm{k}$ be a scalar, then

i) If A is a square matrix of order ‘n’ and k is a scalar quantity then the trace of multiplication of k and A is equal to the Multiplication of k into the trace of A.

Tr(kA)=k·Tr(A)

ii)If A is the square matrix of order ‘n x m’ and B be square matric of order ‘m x n then, the trace of the sum( or subtraction) of Matrix A and B is equal to the sum (or subtraction) of Trace of A and Trace of B.

Tr(A ± B) = Tr(A) ± Tr(B)

iii) If A is the square matrix of order ‘n x m’ and B be square matric of order 'm x n' then, the Trace of Matrix AB is equal to the Trace of matrices B A.

Tr(AB) = Tr(BA)

iv) If A is square matrices of order ‘n’ then, the Trace of Matrix A is equal to the Trace of the transpose of Matrix A.

Tr(A) = Tr(A’)

v) If A is the square matrix of order ‘n x m’ and B be square matric of order ‘m x n’ then, the trace of Matrix AB is not equal to the Trace of Matrix A multiplied by the Trace of Matrix B.

Tr(AB) ≠ Tr(A).Tr(B)

vi) if I is the Identity matrix of order ‘n’ then the trace of the identity matrix is equal to n.

Tr(I) =n

vii) Trace of zero or null matrix is always zero.

Tr(0)=0 S

Recommend Video Based on Trace of a Matrix:

Solved Examples Based on Trace of Matrices

Example 1: Let and $2 A-B=\left[\begin{array}{ccc}2 & -1 & 5 \\ 2 & -1 & 6 \\ 0 & 1 & 2\end{array}\right]$. If $\operatorname{Tr}(\mathrm{A})$ denotes the sum of all diagonal elements of the matrix $A$, then $\operatorname{Tr}(\mathrm{A})-\operatorname{Tr}(\mathrm{B})$ has a value equal to [JEE MAIN 2021]

1) 1

2) 2

3) 0

4) 3

Solution:

$\begin{aligned} & A+2 B=\left(\begin{array}{ccc}1 & 2 & 0 \\ 6 & -3 & 3 \\ -5 & 3 & 1\end{array}\right) \\ & 2 A-B=\left(\begin{array}{ccc}2 & -1 & 5 \\ 2 & -1 & 6 \\ 0 & 1 & 2\end{array}\right) \\ & \Rightarrow 4 A-2 B=\left(\begin{array}{ccc}4 & -2 & 10 \\ 4 & -2 & 12 \\ 0 & 2 & 4\end{array}\right)\end{aligned}$

Add (1) and (2), we get

$\begin{equation}
\begin{aligned}
& \Rightarrow 5 \mathrm{~A}=\left(\begin{array}{ccc}
5 & 0 & 10 \\
10 & -5 & 15 \\
-5 & 5 & 5
\end{array}\right) \\
& A=\left(\begin{array}{ccc}
1 & 0 & 2 \\
2 & -1 & 3 \\
-1 & 1 & 1
\end{array}\right) \text { and } 2 A=\left(\begin{array}{ccc}
2 & 0 & 4 \\
4 & -2 & 6 \\
-2 & 2 & 2
\end{array}\right) \\
& \therefore \mathrm{B}=\left(\begin{array}{ccc}
2 & 0 & 4 \\
4 & -2 & 6 \\
-2 & 2 & 2
\end{array}\right)-\left(\begin{array}{ccc}
2 & -1 & 5 \\
2 & -1 & 6 \\
0 & 1 & 2
\end{array}\right) \\
& \mathrm{B}=\left(\begin{array}{ccc}
0 & 1 & -1 \\
2 & -1 & 0 \\
-2 & 1 & 0
\end{array}\right) \\
& \operatorname{tr}(\mathrm{A})=1-1+1=1 \\
& \operatorname{tr}(\mathrm{B})=-1 \\
& \operatorname{tr}(\mathrm{A})=1 \text { and } \operatorname{tr}(\mathrm{B})=-1 \\
& \therefore \operatorname{tr}(\mathrm{A})-\operatorname{tr}(\mathrm{B})=2
\end{aligned}
\end{equation}$

Hence, the answer is the option 2.

Example 2 The number of all $3 \times 3$ matrices A, with entries from the set $\{-1,0,1\}$ such that the sum of the diagonal elements of $A A^T$ is

1) 672

2)512

3)1024

4)256

Solution

Let matrix $\mathrm{A}$ be
$
\begin{aligned}
& A=\left[\begin{array}{lll}
a & b & c \\
d & e & f \\
g & h & i
\end{array}\right] \\
& A^T=\left[\begin{array}{lll}
a & d & g \\
b & e & h \\
c & f & i
\end{array}\right] \\
& \operatorname{trace}\left(A A^T\right)=a^2+b^2+c^2+d^2+e^2+f^2+g^2+h^2+i^2=3
\end{aligned}
$

So out of 9 elements, 3 elements must be equal to 1 or −1, and the rest elements must be 0.

Possible causes

$\begin{equation}
\begin{array}{cl}
0,0,0,0,0,0,1,1,1 & \rightarrow \text { Total possibilities }={ }^9 C_6 \\
0,0,0,0,0,0,-1,-1,-1 & \rightarrow \text { Total possibilities }={ }^9 C_6 \\
0,0,0,0,0,0,1,1,-1 & \rightarrow \text { Total possibilities }={ }^9 C_6 \times 3 \\
0,0,0,0,0,0,-1,1,-1 & \rightarrow \text { Total possibilities }={ }^9 C_6 \times 3 \\
\text { Total number of cases }={ }^9 C_6 \times 8=672
\end{array}
\end{equation}$

Hence, the answer is the option 1

Example 3 Let $\mathrm{A}$, other than $l$ or $-l$, be a $2 \times 2$ real matrix such that $a^2=l, l_{\text {being the unit matrix. Let }} \operatorname{Tr}(A)$ be the sum of diagonal elements of $\mathrm{A}$. [JEE MAIN 2013]

Statement 1: $\operatorname{Tr}(A)=0$
Statement 2: $\operatorname{det}(A)=-1$

1)statement 1 is true; statement 2 is false.

2) statement 1 is true; statement 2 is true; statement 2 is not the correct explanation for statement 1

3)statement 1 is true; statement 2 is true; statement 2 is the correct explanation for statement 1

4)statement 1 is false; statement 2 is true;

Solution:

$
\begin{aligned}
& {\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]} \\
& {\left[\begin{array}{ll}
a^2+b c & a b+b d \\
a c+c d & b c+d^2
\end{array}\right]=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]} \\
& b(a+d)=0, b=0 \text { or } a=-d \\
& c(a+d)=0, c=0 \text { or } a=-d \\
& a^2+b c=1, b c+d^2=1 \\
&
\end{aligned}
$
' $a$ ' and 'd' are the diagonal element, $a+d=0$
Statement 1 is true
Now, $\operatorname{det}(\mathrm{A})=\mathrm{ad}-\mathrm{bc}$
Now, from (3) $a^2+b c=1$ and $d^2+b c=1$
So, $a^2-d^2=0$
Adding $a^2+d^2+2 b c=2$
$
=(a+d)^2-2 a d+2 b c=2
$
or $0-2(a d-b c)=2$
So, $a d-b c=1 \Rightarrow \operatorname{det}(A)=-1$
So, statement -2 is also true.
But statement -2 is not the correct explanation of statement-I

Hence, the answer is option 2

Example 4: If the element of a matrix A is defined by $a_{i j}=i^2-j^2 \text { and } \mathrm{A} \text { is a square matrix of order } 3 \times 3 \text {. Then } \operatorname{tr}(A)=$

1) 14

2) 28

3) 0

4) 5

Solution:

Trace of a Matrix -

$
\operatorname{tr}(A)=\sum_{i=1}^n a_{i i}
$
if $A=\left[a_{i j}\right]_{n \times n}$
The sum of the elements of a square matrix $A$ lying along the principal diagonal
Since $a_{11}=0=a_{22}=a_{33}$
$
\operatorname{tr}(A)=a_{11}+a_{22}+a_{33}=0
$

Hence, the answer is option 3.

Example 5: Let A be a $2 \times 2$ real matrix with entries from $\{0,1\}$ and $|A| \neq 0$ Consider the following two statements :
(P) If $\mathrm{A} \neq \mathrm{I}_2$, then $|\mathrm{A}|=-1$
(Q) If $|\mathrm{A}|=1$, then $\operatorname{tr}(\mathrm{A})=2$, where denotes 2 × 2 identity matrix and tr(A) denotes the sum of the diagonal entries of A. Then:

1) (P) is false and (Q) is true

2) Both (P) and (Q) are false

3) (P) is true and (Q) is false

4) Both (P) and (Q) are true

Solution:

$
\begin{aligned}
& |A| \neq 0 \\
& \text { For }(\mathrm{P}): \mathrm{A} \neq \mathrm{I}_2
\end{aligned}
$

So, $\mathrm{A}=\left[\begin{array}{ll}0 & 1 \\ 1 & 0\end{array}\right]$ or $\left[\begin{array}{ll}1 & 1 \\ 1 & 0\end{array}\right]$ or $\left[\begin{array}{ll}0 & 1 \\ 1 & 1\end{array}\right]$ or $\left[\begin{array}{ll}1 & 1 \\ 0 & 1\end{array}\right]$ or $\left[\begin{array}{ll}1 & 0 \\ 1 & 1\end{array}\right]$ $|A|$ can be -1 or 1

So (P) is false
For $(\mathrm{Q}):|\mathrm{A}|=1$
$
\begin{aligned}
& \mathrm{A}=\left[\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right] \text { or }\left[\begin{array}{ll}
1 & 1 \\
0 & 1
\end{array}\right] \text { or }\left[\begin{array}{ll}
1 & 0 \\
1 & 1
\end{array}\right] \\
& \Rightarrow \operatorname{tr}(\mathrm{A})=2 \\
& \Rightarrow \mathrm{Q} \text { is true }
\end{aligned}
$

Hence, the answer is the option 1

Frequently Asked Questions (FAQs)

1. Is the trace of a matrix always a scalar?

Yes, the trace of a matrix is always a scalar (single number), regardless of the matrix's size, as long as it's a square matrix.

2. What's the relationship between eigenvalues and the trace of a matrix?

The trace of a matrix is equal to the sum of its eigenvalues. This property holds for any square matrix, even if some eigenvalues are complex or repeated.

3. How does matrix addition affect the trace?

The trace of the sum of two matrices is equal to the sum of their individual traces. In other words, tr(A + B) = tr(A) + tr(B) for any two square matrices A and B of the same size.

4. What happens to the trace when you multiply a matrix by a scalar?

When you multiply a matrix by a scalar k, the trace is multiplied by that same scalar. So, tr(kA) = k * tr(A) for any square matrix A and scalar k.

5. Is the trace of a matrix always positive?

No, the trace of a matrix can be positive, negative, or zero, depending on the values of the elements on its main diagonal.

6. How does matrix multiplication affect the trace?

Unlike addition, the trace of a product is not generally equal to the product of traces. However, the trace of AB is equal to the trace of BA for any two square matrices A and B of the same size.

7. How is the trace related to the determinant of a 2x2 matrix?

For a 2x2 matrix A = [a b; c d], the characteristic equation is λ² - tr(A)λ + det(A) = 0. This shows a direct relationship between trace, determinant, and eigenvalues for 2x2 matrices.

8. Can you determine if a matrix is singular from its trace?

No, you can't determine if a matrix is singular solely from its trace. A matrix can have a non-zero trace and still be singular, or have a zero trace and be non-singular.

9. What's the relationship between the trace and the Frobenius norm of a matrix?

The square of the Frobenius norm of a matrix A is equal to the trace of A*A', where A' is the conjugate transpose of A.

10. What's the trace of a projection matrix?

The trace of a projection matrix is equal to its rank, which is the dimension of the subspace it projects onto.

11. How do you calculate the trace of a 3x3 matrix?

For a 3x3 matrix A = [a_ij], the trace is calculated as: tr(A) = a_11 + a_22 + a_33, where a_ii represents the element at the i-th row and i-th column.

12. What's the trace of a diagonal matrix?

The trace of a diagonal matrix is the sum of its diagonal elements, which are the only non-zero elements in the matrix.

13. Can two different matrices have the same trace?

Yes, many different matrices can have the same trace. The trace only depends on diagonal elements, so matrices with different off-diagonal elements can still have the same trace.

14. Is the trace of a matrix always equal to the trace of its transpose?

Yes, the trace of a matrix is always equal to the trace of its transpose. This is because transposition doesn't change the main diagonal elements.

15. What's the trace of a nilpotent matrix?

The trace of a nilpotent matrix is always 0. This is because all eigenvalues of a nilpotent matrix are 0, and the trace is the sum of eigenvalues.

16. What is the trace of a matrix?

The trace of a matrix is the sum of all elements on its main diagonal (from top-left to bottom-right). It's only defined for square matrices.

17. Can you find the trace of a non-square matrix?

No, the trace is only defined for square matrices. Non-square matrices don't have a main diagonal that spans the entire matrix, so the concept of trace doesn't apply.

18. What's the trace of an identity matrix?

The trace of an n x n identity matrix is always n, because all diagonal elements are 1, and there are n of them.

19. What's the significance of the trace in linear transformations?

In linear algebra, the trace represents the sum of the eigenvalues of a linear transformation. It's invariant under similarity transformations, making it useful for characterizing linear operators.

20. What's the trace of a zero matrix?

The trace of a zero matrix (a matrix where all elements are 0) is always 0, regardless of its size.

21. How is the trace used in quantum mechanics?

In quantum mechanics, the trace of a density matrix represents the total probability, which must equal 1 for a properly normalized quantum state.

22. How is the trace used in optimization problems?

The trace often appears in optimization problems involving matrices, such as in the formulation of certain machine learning algorithms like Principal Component Analysis (PCA).

23. How does the trace relate to matrix similarity?

Similar matrices always have the same trace. If B = P⁻¹AP, then tr(B) = tr(A) for any invertible matrix P.

24. How does the trace behave under matrix powers?

The trace of matrix powers follows the pattern: tr(A²) = tr(A)² - 2tr(A²/2), where A²/2 is the matrix whose square is A².

25. How is the trace used in statistics?

In multivariate statistics, the trace of a covariance matrix represents the total variance of a set of variables.

26. What's the trace of a rotation matrix in 2D?

The trace of a 2D rotation matrix is always 2cos(θ), where θ is the angle of rotation.

27. How does the trace relate to the characteristic polynomial of a matrix?

The trace appears as the coefficient of the second-highest degree term (with a negative sign) in the characteristic polynomial of a matrix.

28. What's the trace of a permutation matrix?

The trace of a permutation matrix is equal to the number of fixed points in the permutation (elements that don't change position).

29. How does the trace behave under matrix exponentiation?

The trace of the matrix exponential e^A is equal to e^tr(A) only when A is a diagonal matrix.

30. What's the relationship between the trace and matrix logarithm?

For a positive definite matrix A, tr(log(A)) = log(det(A)), where log(A) is the matrix logarithm.

31. What's the trace of a Hermitian matrix?

The trace of a Hermitian matrix is always a real number, even though the matrix may contain complex entries.

32. How does the trace relate to the rank of a matrix?

While there's no direct relationship, the trace of A*A' (where A' is the conjugate transpose of A) is equal to the sum of squares of singular values of A, which is related to its rank.

33. What's the trace of a skew-symmetric matrix?

The trace of a skew-symmetric matrix is always 0, because its diagonal elements are all zero.

34. How is the trace used in the study of Lie algebras?

In Lie algebra theory, the trace form (or Killing form) is used to classify simple Lie algebras and is defined using the trace of certain matrix products.

35. What's the relationship between the trace and matrix factorizations?

In many matrix factorizations, such as LU or QR decomposition, the product of the traces of the factor matrices is equal to the trace of the original matrix.

36. How does the trace behave under Kronecker product?

The trace of the Kronecker product of two matrices A and B is equal to the product of their individual traces: tr(A ⊗ B) = tr(A) * tr(B).

37. What's the trace of a matrix raised to a negative power?

For an invertible matrix A, tr(A⁻¹) is equal to the sum of reciprocals of eigenvalues of A.

38. How is the trace used in defining matrix norms?

The trace norm (or nuclear norm) of a matrix A is defined as the sum of its singular values, which can be expressed as tr((A*A')^(1/2)).

39. What's the trace of a complex matrix?

The trace of a complex matrix is the sum of its diagonal elements, which may be complex numbers. However, for Hermitian matrices, the trace is always real.

40. How does the trace relate to the determinant for 3x3 matrices?

For a 3x3 matrix A, its characteristic polynomial is λ³ - tr(A)λ² + (1/2)(tr(A)² - tr(A²))λ - det(A) = 0, showing a relationship between trace, determinant, and matrix powers.