Trigonometric Identities

In trigonometry, there are six trigonometric ratios, which formulate relations with each other. There are relationships between different trigonometric ratios such as sine, cosine and tangent, etc. The identities are generated by observing and analyzing results from the Pythagoras theorem and the relation between the sides of a right-angled triangle.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

In this article, we will learn more about the trigonometric identities. This category comes under Trigonometry. It is one of the major chapter in the syllabus of Class 11th Mathematics. Question related to trigonometry doesn’t always come directly but also the concepts of trigonometry are mixed and asked with some other concepts as well. It is crucial for both the board exams and competitive exams such as JEE Main, WBJEE, BITSAT, etc.

What are Trigonometric Identities?

Trigonometric Identities are the relationship which involve different trigonometric ratios which hold true for all the value of angles within the equation. These identities represent the relationship between the angles of a right angle triangle, and its sides. Here the ratios are defined on the basis of sides of a right angled triangle, such as the adjacent side, opposite side and the longest side(being hypotenuse). There are six trigonometric ratios namely as the sine, cosine, tangent, cotangent, secant and cosecant.

List of Trigonometric Identities

In the branch of trigonometry, all trigonometric identities help in solving different variety of problems. There are several identities which will play crucial role in order to simplify trigonometric equations and in proving theorems. It is one of the important tools to solve complex problems in geometry, calculus, physics. Below are some of the basic trigonometric identities formula:

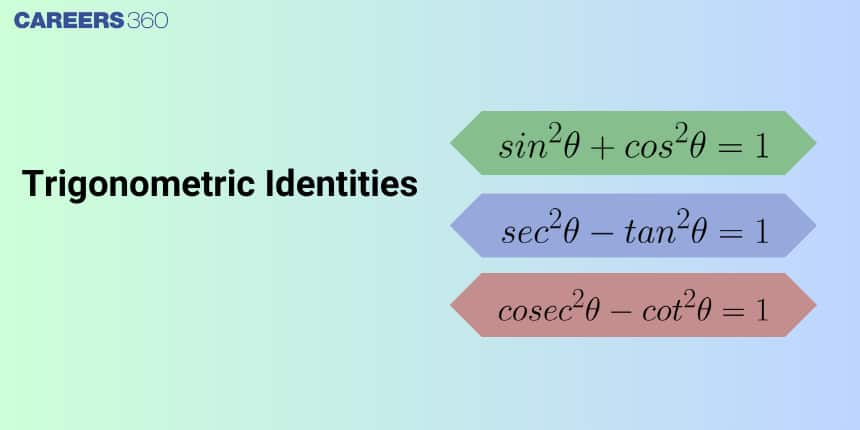
1. Pythagorean theorem identities

The trigonometric identities which are expressed by using the Pythagoras theorem, involving a right angle triangle, its sides, angles.

$\begin{aligned} & \sin^2 t + \cos^2 t = 1 \\ & 1 + \tan^2 t = \sec^2 t \\ & 1 + \cot^2 t = \csc^2 t \\ & \tan t = \frac{\sin t}{\cos t}, \quad \cot t = \frac{\cos t}{\sin t} \end{aligned}$

2. Reciprocal identities

The reciprocal identities are the set of some basic trigonometric ratios which show the reciprocal relations between the ratios. It helps to write the trigonometric ratios such as sine, cosine and tangent in terms of the reciprocal functions such as cosecant, secant and cotangent.

Below listed are the reciprocal trigonometric identities:

$\begin{aligned} & \text{Cosecant} \quad \csc t = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{1}{\sin t} \\ & \text{Secant} \quad \sec t = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{1}{\cos t} \\ & \text{Cotangent} \quad \cot t = \frac{\text{adjacent}}{\text{opposite}} = \frac{1}{\tan t} \end{aligned}$

3. Addition of angles trignometric identites

Addition of trigonometric identities also refer to as the sum formulae. It helps us to calculate the trigonometric function for sum of two angles, which helps to simplify expressions and solving equations containing many angles.

Below are the basic addition identities:

There are three trigonometric identities related to the Addition of angles.
If $A$ and $B$ are two angles, then,

$\begin{aligned} & \text{For sine:} \quad \sin(A + B) = \sin A \cos B + \cos A \sin B \\ & \text{For cosine:} \quad \cos(A + B) = \cos A \cos B - \sin A \sin B \\ & \text{For tangent:} \quad \tan(A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \end{aligned}$

4. Difference of angles trigonometric identities

Difference of angles trigonometric identities, helps in finding the trigonometric values where there angles are subtracted. These identities are also known as the subtraction formulae.

There are three trigonometric identities related to the difference in angles.
If $A$ and $B$ are two angles, then they follow:
$\begin{aligned} & \text{For sine:} \quad \sin(A - B) = \sin A \cos B - \cos A \sin B \\ & \text{For cosine:} \quad \cos(A - B) = \cos A \cos B + \sin A \sin B \\ & \text{For tangent:} \quad \tan(A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \end{aligned}$

5. Double-angle trignometric identities

The double-angle trignometric identities is used to transform the trignometric ratios of double angles into the trignometric ratios of single angles. The double angle trigonometric function helps us to solve equations, simplify expressions. These identities express functions of double angles($2A) in terms of ange ($A$).The double angle identities are derived by using the sum formula.
If A is the angle of the triangle, there are identities listed below:

$\begin{aligned} \quad \sin(2A) = 2 \sin A \cos A \\ \quad \cos(2A) = \cos^2 A - \sin^2 A \\ \cos(2A) = 2 \cos^2 A - 1 \\ \cos(2A) = 1 - 2 \sin^2 A \\ \quad \tan(2A) = \frac{2 \tan A}{1 - \tan^2 A} \end{aligned}$

6. Trigonometric identities of allied angles

Two angles are called allied if their sum or difference is a multiple of $\pi / 2(90^\circ)$. These identities help in simplifying different expressions to calculate the trigonometric values for the non-standard angles.

For $\theta$ as angle, below are some trigonometric identities of allied angles:
$\begin{aligned} & \text{For } 90^\circ - \theta \text{ or } \frac{\pi}{2} - \theta: \\ & \sin(90^\circ - \theta) = \cos \theta \\ & \cos(90^\circ - \theta) = \sin \theta \\ & \tan(90^\circ - \theta) = \cot \theta \\ & \cot(90^\circ - \theta) = \tan \theta \\ & \sec(90^\circ - \theta) = \csc \theta \\ & \csc(90^\circ - \theta) = \sec \theta \\ \\ & \text{For } 180^\circ - \theta \text{ or } \pi - \theta: \\ & \sin(180^\circ - \theta) = \sin \theta \\ & \cos(180^\circ - \theta) = -\cos \theta \\ & \tan(180^\circ - \theta) = -\tan \theta \\ & \cot(180^\circ - \theta) = -\cot \theta \\ \\ & \text{For } 180^\circ + \theta \text{ or } \pi + \theta: \\ & \sin(180^\circ + \theta) = -\sin \theta \\ & \cos(180^\circ + \theta) = -\cos \theta \\ & \tan(180^\circ + \theta) = \tan \theta \\ & \cot(180^\circ + \theta) = \cot \theta \\ \\ & \text{For } 360^\circ - \theta \text{ or } 2\pi - \theta: \\ & \sin(360^\circ - \theta) = -\sin \theta \\ & \cos(360^\circ - \theta) = \cos \theta \\ & \tan(360^\circ - \theta) = -\tan \theta \\ \end{aligned}$

7. Triple-angle Trigonometric identities

Triple angle trigonometric identities are used to express functions of a triple angle say $3A$, in terms of the angle $A$.
If $A$ is the angle of the triangle, below are the triple angle identities:

$\begin{aligned} & \text{For sine:} \quad \sin(3A) = 3 \sin A - 4 \sin^3 A \\ & \text{For cosine:} \quad \cos(3A) = 4 \cos^3 A - 3 \cos A \\ & \text{For tangent:} \quad \tan(3A) = \frac{3 \tan A - \tan^3 A}{1 - 3 \tan^2 A} \end{aligned}$

8. Trigonometric identities of supplementary angles

Two angles are called supplementary angles if their sum is 180. These identities help us to calculate the value of a supplementary trigonometric angle in terms of the trigonometric function of the angle itself.
Below are the trigonometric identities of supplementary angles:
$\begin{aligned} & \text{For sine:} \quad \sin(180^\circ - \theta) = \sin \theta \\ & \text{For cosine:} \quad \cos(180^\circ - \theta) = -\cos \theta \\ & \text{For tangent:} \quad \tan(180^\circ - \theta) = -\tan \theta \\ & \text{For cotangent:} \quad \cot(180^\circ - \theta) = -\cot \theta \\ & \text{For secant:} \quad \sec(180^\circ - \theta) = -\sec \theta \\ & \text{For cosecant:} \quad \csc(180^\circ - \theta) = \csc \theta \\ \end{aligned}$

9. Sum-product trigonometric identities

The Sum/Difference identity is used to express the sum or difference of sine and cosine functions into the Product of sine and cosine functions. Below are some Product sum trigonometric identities :

Sum of Sines: $\quad \sin (A+B)=\sin A \cos B+\cos A \sin B$

Difference of Sines: $\quad \sin (A-B)=\sin A \cos B-\cos A \sin B$

Sum-to-Product for Sine: $\sin A+\sin B=2 \sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)$

$\sin A-\sin B=2 \cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)$

Sum of Cosines: $\quad \cos (A+B)=\cos A \cos B-\sin A \sin B$

Difference of Cosines: $\quad \cos (A-B)=\cos A \cos B+\sin A \sin B$

Sum-to-Product for Cosine: $\quad \cos A+\cos B=2 \cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)$

$\cos A-\cos B=-2 \sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)$

Tangent of Sum: $\quad \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}$

Tangent of Difference: $\quad \tan (A-B)=\frac{\tan A-\tan B}{1+\tan A \tan B}$

10. Trigonometric identities of the opposite angle

The trigonometric identities for opposite angles are used to understand how the functions sine, cosine and tangent change when they are reflected across origin. Below are some trigonometric identities of opposite angles:
$\begin{aligned} & \sin(-A) = -\sin A \\ & \cos(-A) = \cos A \\ & \tan(-A) = -\tan A \\ & \cot(-A) = -\cot A \\ & \sec(-A) = \sec A \\ & \csc(-A) = -\csc A \end{aligned} $

11. Ratio Trigonometric Identities

Ratio trigonometric identities are formed by using different trigonometric functions such as $sin\theta$ or $cos\theta$.

The trigonometric ratio identities are:

• $\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}$
• $\cot(\theta) = \frac{\cos(\theta)}{\sin(\theta)} = \frac{1}{\tan(\theta)}$

Triangle Identities (Sine, Cosine, Tangent rule)

If the identities or equations are applicable for all the triangles and not just for right triangles, then they are the triangle identities. These identities will include:
1) Sine Law
2) Cosine Law
3) Tangent Law

Sine Rule
The ratio of the sine of one of the angles to the length of its opposite side will be equal to the other two ratios of the sine of the angle measured to the opposite side.

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$

Cosine Rule
For a triangle with angles $\mathrm{A}, \mathrm{B}$, and $C$ , and opposite corresponding sides $\mathrm{a}, \mathrm{b}$, and c , respectively, the Law of Cosines is given as three equations.

$\cos A=\frac{b^2+c^2-a^2}{2 b c} \quad \cos B=\frac{a^2+c^2-b^2}{2 a c} \quad \cos C=\frac{a^2+b^2-c^2}{2 a b}$

Tangent Rule or Napier's Analogy
Tangent rule is used to form a relation between lengths of side of triangle and tangent of the angles. For any $\triangle A B C$,

$\tan \left(\frac{A-B}{2}\right)=\frac{a-b}{a+b} \cot \frac{C}{2}$

Important Notes on Trigonometry Identities

• To write the trigonometric ratios of complementary angles, we consider the following as pairs: (sin, cos), (cosec, sec), and (tan, cot).
• While writing the trigonometric ratios of supplementary angles, the trigonometric ratio won't change. The sign can be decided using the fact that only sin and cosec are positive in the second quadrant where the angle is of the form $(180-θ)$.
• There are 3 formulas for the $cos 2x$ formula. You can remember just the first one because the other two can be obtained by the Pythagorean identity $sin^2x+cos^2x=1$.
• The half-angle formula of tan is obtained by applying the identity $tan = \frac{sin}{cos}$ and then using the half-angle formulas of $sin$ and $cos$.

Recommended Video Based on Trigonometric Identities

Solved Examples Based on Trigonometric Identities

Example 1: For a triangle $A B C$, the value of $\cos 2 A+\cos 2 B+\cos 2 C$ is least. If its inradius is 3 and incentre is $M$, then which of the following is NOT correct? [JEE MAINS 2023]
1) The perimeter of $\triangle A B C$ is $18 \sqrt{3}$
2) $\sin 2 A+\sin 2 B+\sin 2 C=\sin A+\sin B+\sin C$
3) $\overrightarrow{M A} \cdot \overrightarrow{M B}=-18$
4) The area of $\triangle A B C$ is $\frac{27 \sqrt{3}}{2}$

Solution:
Let P
$=\cos 2 \mathrm{~A}+\cos 2 \mathrm{~B}+\cos 2 \mathrm{C}$
$=2 \cos (\mathrm{A}+\mathrm{B}) \cos (\mathrm{A}-\mathrm{B})+2 \cos ^2 \mathrm{C}-1$
$=2 \cos (\pi-\mathrm{C}) \cos (\mathrm{A}-\mathrm{B})+2 \cos ^2 \mathrm{C}-1$
$=-2 \cos \mathrm{C}[\cos (\mathrm{A}-\mathrm{B})+\cos (\mathrm{A}+\mathrm{B})]-1$
$=-1-4 \cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}$
for $P$ to be the minimum
$\cos \mathrm{A} \cos \mathrm{B} \cos \mathrm{C}$ must be maximum
$\Rightarrow \triangle \mathrm{ABC}$ is an equilateral triangle

Let the side length of the triangle be a

$\begin{aligned} & \tan \theta=\frac{3}{a / 2} \\ & \Rightarrow \frac{1}{\sqrt{3}}=\frac{6}{a} \Rightarrow a=6 \sqrt{3} \\ & \text { area of triangle }=\frac{\sqrt{3}}{4} \mathrm{a}^2 \\ & =\frac{\sqrt{3}}{4}(108)=27 \sqrt{3}\end{aligned}$

Hence, the answer is option 4.

Example 2: Let $f_k(x)=\frac{1}{k}\left(\sin ^k+\cos ^k x\right)$ for $\mathrm{k}=1,2,3, \ldots .$. Then for all real values of x , the value of $f_4(x)-f_6(x)$ is equal to:
1) $\frac{1}{4}$
2) $\frac{-1}{12}$
3) $\frac{5}{12}$
4) $\frac{1}{12}$

Solution:

$\begin{aligned} & f_4(x)=\frac{1}{4}\left(\sin ^4 x+\cos ^4 x\right) \\ & =\frac{1}{4}\left[\left(\sin ^2+\cos ^2 x\right)^2-2 \sin ^2 x \cos ^2 x\right] \\ & =\frac{1}{4}-\frac{1}{2} \sin ^2 x \cos ^2 x \\ & f_6(x)=\frac{1}{6}\left(\sin ^6 x+\cos ^6 x\right) \\ & =\frac{1}{6}\left[\left(\sin ^2 x+\cos ^2 x\right)^3\right]-3 \sin ^4 x \cos ^2 x-3 \sin ^2 x \cos ^4 x \\ & =\frac{1}{6}\left[1-3 \sin ^2 x \cos ^2 x\left(\sin ^2 x+\cos ^2 x\right)\right] \\ & =\frac{1}{6}-\frac{1}{2} \sin ^2 x \cos ^2 x \\ & f_4(x)-f_6(x)=\frac{1}{4}-\frac{1}{6}=\frac{1}{12}\end{aligned}$

Hence, the answer is option 4.

Example 3: If $15 \sin ^4 \alpha+10 \cos ^4 \alpha=6$ for some $\alpha \epsilon R$, then the value of $27 \sec ^6 \alpha+8 \operatorname{cosec}^6 \alpha$ is equal to: [JEE MAINS 2021]
1) 350
2) 250
3) 400
4) 500

Solution
$\begin{aligned} & 15 \sin^4 \alpha + 10 \cos^4 \alpha = 6 \\ & 15 \sin^4 \alpha + 10 \cos^4 \alpha = 6\left(\sin^2 \alpha + \cos^2 \alpha\right)^2 \\ & \left(3 \sin^2 \alpha - 2 \cos^2 \alpha\right)^2 = 0 \\ & \tan^2 \alpha = \frac{2}{3} \quad \Rightarrow \quad \cot^2 \alpha = \frac{3}{2} \\ & \Rightarrow 27 \sec^6 \alpha + 8 \csc^6 \alpha \\ & = 27\left(\sec^6 \alpha\right)^3 + 8\left(\csc^6 \alpha\right)^3 \\ & = 27\left(1 + \tan^2 \alpha\right)^3 + 8\left(1 + \cot^2 \alpha\right)^3 \\ & = 250 \end{aligned}$

Hence, the answer is option 3.

Example 4: Let $S=\left\{\theta \epsilon[-2 \pi, 2 \pi]: 2 \cos ^2 \theta+3 \sin \theta=0\right\}$. Then the sum of the elements of $S$ is: [JEE MAINS 2019]
1) $\frac{13 \pi}{6}$
2) $\frac{5 \pi}{3}$
3) $2 \pi$
4) $\pi$

Solution:

Given equation

$\begin{aligned} & 2 \cos^2 \theta + 3 \sin \theta = 0 \\ & 2 - 2 \sin^2 \theta + 3 \sin \theta = 0 \end{aligned}$

Or
$\begin{aligned} & 2 \sin^2 \theta - 3 \sin \theta - 2 = 0 \\ & \sin \theta = -\frac{1}{2} \quad \text{or} \quad \sin \theta = 2 \\ & \sin \theta \neq 2 \end{aligned}$
because solution is $[-2 \pi, 2 \pi]$
$\begin{aligned} & -\pi + \frac{\pi}{6}, \quad \frac{-\pi}{6}, \quad \pi + \frac{\pi}{6}, \quad 2\pi - \frac{\pi}{6} \\ & \text{Sum} = 2\pi \end{aligned}$

Hence, the answer is option 3.

Example 5: If $\frac{\sqrt{2} \sin \alpha}{\sqrt{1+\cos 2 \alpha}}=\frac{1}{7}$ and $\sqrt{\frac{1-\cos 2 \beta}{2}}=\frac{1}{\sqrt{10}}, \alpha, \beta \space\epsilon\left(0, \frac{\pi}{2}\right)$, then $\tan (\alpha+2 \beta)$ is equal to

1) 0

2) 1

3) 0.5

4) 2

Solution:

$\begin{aligned} & \frac{\sqrt{2} \sin \alpha}{\sqrt{2} \cos \alpha}=\frac{1}{7} \\ & \tan \alpha=\frac{1}{7} \\ & \sin \beta=\frac{1}{\sqrt{10}} \\ & \tan \beta=\frac{1}{\sqrt{3}} \\ & \tan 2 \beta=\frac{2 \cdot \frac{1}{3}}{1-\frac{1}{9}}=\frac{\frac{2}{3}}{\frac{8}{9}}=\frac{3}{4} \\ & \tan (\alpha+2 \beta)=\frac{\tan \alpha+\tan 2 \beta}{1-\tan \alpha \tan 2 \beta}=1\end{aligned}$

Hence, the answer is option 2.