Trigonometric Inequality - Evaluation and Method of Solving Problem

An inequality involving trigonometric functions of an unknown angle is called a trignometric inequality. Finding a solution to the inequality means determining the values of the variable $arc (x)$, whose trigonometric functions make the inequality true. In real life, we use trignometric inequality to measure the distance between landmarks, in the satellite navigation system.

In this article, we will cover the concept of trigonometric Inequality. This category falls under the broader category of Trigonometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), Six questions have been asked on this topic.

What are the Trigonometric Equations?

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Trigonometric equations are satisfied only for some values (finite or infinite in number) of the angles. A value of the unknown angle that satisfies the given trigonometric equation is called a solution or a root of the equation. For example, equation $2 \sin x=1$ is satisfied by $x=\pi / 6$ is the solution of the equation between $o$ and $\pi$. The solutions of a trigonometric equation lying in the interval $[0, \pi)$ are called principal solutions.

What is the Trigonometric Inequality?

An inequality involving trigonometric functions of an unknown angle is called a trigonometric inequality. The trigonometric inequation is of the type f(x) ≥ a or f(x) ≤ a, where f(x) is some trigonometric ratio. The solution sets of trigonometric inequalities are expressed in intervals.

Types of Trigonometric Inequalities

1) $\sin x>a($ or $<a)$
2) $\cos x>a($ or $<a)$
3) $\tan x>a($ or $<a)$
4) $\cot x>a($ or $<a)$

Steps to Solve Trigonometric Inequalities

Consider inequality $f(x)>g(x)$ or $f(x)<g(x)$, where at least one of the functions $f(x)$ and $g(x)$ is a trigonometric function.

To solve such inequalities, we draw the graphs of $y=f(x)$ and $y=g(x)$.
The solution set of $f(x)>g(x)$ is the set of values of $x$ for which the graph of $y=f(x)$ lies above the graph of $y=g(x)$.

The solution set of $f(x)<g(x)$ is the set of values of $x$ for which the graph of $y=f(x)$ lies below the graph of $y=g(x)$.

The following steps should be taken to solve such types of inequations

1. 1. Draw the graph of $f(x)$ in an interval length equal to the fundamental period of $f(x)$.
   2. Draw the line $y=a$.
   3. Take the portion of the graph for which the inequation is satisfied.
   4. To generalize, add $n T(n \in I)$, where $T$ is the fundamental period of $f(x)$.

Example

What is the solution set of inequality $\cos x>1 / 2 ?$

Solution

1. Fundamental period of $\cos (x)$ is $2 \pi$, so we draw its graph in any interval of length $2 \pi$. Here we are drawing the graph in $-\pi$ to $\pi$
2. When $\cos x=1 / 2$, then two values of $x$ between $-\pi$ and $\pi$ is $-\pi / 3$ and $\pi / 3$
3. From the graph

4. $\cos x>1 / 2$ for $-\pi / 3<x<\pi / 3$

Now the same interval will repeat in every period of length $2 \pi$
Hence, $\cos x>1 / 2$ when $-\pi / 3+2 n \pi<x<\pi / 3+2 n \pi, n \in I$
Note: We can also interval from 0 to $2 \pi$ instead of $-\pi$ to $\pi$

Solved Examples Based on Trigonometric inequality

Example 1: The value of 36 $\left(4 \cos ^2 9^{\circ}-1\right)\left(4 \cos ^2 27^{\circ}-1\right)\left(4 \cos ^2 81^{\circ}-1\right)\left(4 \cos ^2 243^{\circ}-1\right)$ is [JEE MAINS 2023]

Solution

$4 \cos ^2 \theta-1=4\left(1-\sin ^2 \theta\right)-1=3-4 \sin ^2 \theta=\frac{\sin 3 \theta}{\sin \theta}$ so given expression can be written

Hence, the answer is $36$.

Example 2: What is the range of x for $\sin 2 x>|\cos x|$ where $x \epsilon\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$

Solution

The trigonometric inequation of the type f(x) ≥ a or f(x) ≤ a, where f(x) is some trigonometric ratio, the following steps should be taken to solve such type of equations.:

1. 1. Draw the graph of $f(x)$ in an interval length equal to the fundamental period of $f(x)$.
   2. Draw the line $y=a$.
   3. Take the portion of the graph for which the inequation is satisfied.
   4. To generalize, add $\mathrm{nT}(\mathrm{n} \in \mathrm{I})$ and take union over the set of integers, where $T$ is the fundamental period of $f(x)$.

$
\sin 2 x>|\cos x| \text { where } x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]
$
For the intersection point of $\sin 2 x$ and $\cos x$

$
\begin{gathered}
\sin 2 x=\cos x \\
2 \sin x \cos x=\cos x \\
\cos x(2 \sin x-1)=0 \\
\cos x=0 \rightarrow x=\frac{\pi}{2} \\
\sin x=\frac{\pi}{6}
\end{gathered}
$

From the Graph, We can see that this inequality is satisfied when $x \in\left[\frac{\pi}{6}, \frac{\pi}{2}\right]$
Hence, the answer is

$
x \in\left[\frac{\pi}{6}, \frac{\pi}{2}\right]
$

Example 3: Values of x for $2 \sin x \leq \sin 2 x$ in $x \in\left[0, \frac{\pi}{2}\right]$
Solution

$
2 \sin x \leq \sin 2 x
$
For intersection point

$
\begin{aligned}
& 2 \sin x=\sin 2 x \\
& \sin 2 x-2 \sin x=0 \\
& 2 \sin x \cos x-2 \sin x=0 \\
& 2 \sin x(\cos x-1)=0 \\
& \sin x=0 \text { or } \cos x=1 \\
& x=0
\end{aligned}
$

\text { (As we have to look for } x \text { lying in }[0, \pi / 2] \text { only) }

drawing the Graph of inequalities,

By graph, we can say that no solution for these inequalities Hence, the answer is $x \epsilon \phi$

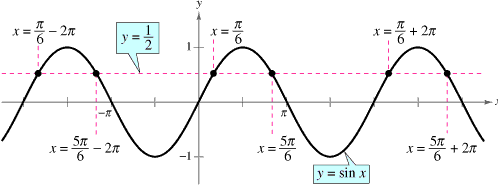
Example 4: If $\sin x>\frac{1}{2}$, then which of the following is true

Solution

We can solve the inequalities with the help of graphs

$
\sin x>\frac{1}{2}
$
In interval $[0,2 \pi), \sin (x)>1 / 2$ for $x$ lying in $(\pi / 6,5 \pi / 6)$

So, the general solution is

$
x \in\left(2 n \pi+\frac{\pi}{6}, 2 n \pi+\frac{5 \pi}{6}\right)
$
Hence, the answer is

$
\left(2 n \pi+\frac{\pi}{6}, 2 n \pi+\frac{5 \pi}{6}\right)
$

Example 5: If $\frac{\sec ^8 \theta}{a}+\frac{\tan ^8 \theta}{b}=\frac{1}{a+b}$, then for every real value of
Solution

$\frac{\sec ^8 \theta}{a}+\frac{\tan ^8 \theta}{b}=\frac{1}{a+b}$

or $\begin{aligned} a^2 \sin ^8 \theta+a b & +b^2=a b\left(\cos ^8 \theta-\sin ^8 \theta\right) \\ & =a b\left(1-2 \sin ^2 \theta \cos ^2 \theta\right) \cos 2 \theta \\ & =a b\left(1-2 \sin ^2 \theta\right)\left(1-\frac{1}{2} \sin ^2 2 \theta\right)\end{aligned}$

$\begin{aligned} & \Rightarrow a^2 \sin ^8 \theta-2 a b \sin ^4 \theta+b^2=-2 a b \sin ^2 \theta \\ &+a b \sin ^2 \theta \sin ^2 2 \theta-\frac{a b}{2} \sin ^2 2 \theta-2 a b \sin ^4 \theta \\ &\left(a \sin ^4 \theta-b\right)^2= 2 a b \sin ^2 \theta\left(-\sin ^2 \theta-1\right. \\ &\left.+2 \sin ^2 \theta \cos ^2 \theta-\cos ^2 \theta\right)\end{aligned}$
$
\begin{aligned}
& \Rightarrow 2 a b \sin ^2 \theta\left(-2+2 \sin ^2 \theta \cos ^2 \theta\right) \geq 0 \\
& \Rightarrow \quad 4 a b \sin ^2 \theta\left(\sin ^4 \theta-\sin ^2 \theta+1\right) \leq 0 \\
& \Rightarrow \quad a b \leq 0
\end{aligned}
$

Hence, the answer is $a b \leq 0$

Summary

Trigonometric inequalities help analyze trigonometric expressions in calculus, geometry, and physics. They have a wide range of applications in physics and mathematics. Understanding trigonometric inequalities helps us analyze various real-life problems.