Trigonometric Integrals

Hameed Misfah Profile image Edit article ×Hameed Misfah - hameed.misfah@entrance360.com is currently editing this Article Stream (*) Subject Level Exam Chapter Paper Type URL /engineering/trigonometric-integral/ Title (*) Trigonometric integral Article Slug (*) trigonometric-integral Content (*)

Trigonometric integral is one of the important parts of Calculus, which applies to measuring the change in the function at a certain point. Mathematically, it forms a powerful tool by which slopes of functions are determined, the maximum and minimum of functions found, and problems on motion, growth, and decay, to name a few. These integration concepts have been broadly applied in branches of mathematics, physics, engineering, economics, and biology.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Trigonometric Integrals
2. Solved Questions Based on Trigonometric Integrals
3. Summary

In this article, we will cover the concept of Trigonometric integral. This concept falls under the broader category of Calculus, a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), three questions have been asked on this concept, including one in 2013, one in 2021, and one in 2023.

Trigonometric Integrals

Integration is the reverse process of differentiation. In integration, we find the function whose differential coefficient is given. The rate of change of a quantity y concerning another quantity x is called the derivative or differential coefficient of y concerning x. Geometrically, the Differentiation of a function at a point represents the slope of the tangent to the graph of the function at that point. These functions are also known as arcus functions, cyclometric functions, or anti-trigonometric functions. These functions are used to get an angle for a given trigonometric value. It refers to the change in the value of the trigonometric function at a certain rate.

(a) Integral of the form

1. $\int \frac{1}{a \cos ^2 x+b \sin ^2 x} d x$
2. $\int \frac{1}{a+b \sin ^2 x} d x$
3. $\int \frac{1}{a+b \cos ^2 x} d x$
4. $\int \frac{1}{a+b \sin ^2 x+c \cos ^2 x} d x$

Working Rule:

Step 1: Divide the numerator and denominator both by $\cos ^2 x$.
Step 2 : Put $\tan x=t, \sec ^2 x \mathrm{dx}=\mathrm{dt}$

This substitution will convert the trigonometric integral into an algebraic integral.

After employing these steps the integral will reduce to the form $\int \frac{f(t) d t}{A t^2+B t+C}$, where $f(t)$ is a polynomial in $t$.
This integral can be evaluated by methods we studied in previous concepts.

(b) Integral of the form

1. $\int \frac{1}{a \sin x+b \cos x} d x$
2. $\int \frac{1}{a+b \sin x} d x$
3. $\int \frac{1}{a+b \cos x} d x$
4. $\int \frac{1}{a \sin x+b \cos x+c} d x$

Working Rule:

Write sin x and cos x in terms of tan (x/2) and then substitute for tan (x/2) = t

i.e.

$\sin x=\frac{2 \tan x / 2}{1+\tan ^2 x / 2}$ and $\cos x=\frac{1-\tan ^2 x / 2}{1+\tan ^2 x / 2}$
replace, $\tan (\mathrm{x} / 2)$ with $t$
by performing these steps the integral reduces to the form
$\int \frac{1}{a t^2+b t+c} \mathrm{dt}$ which can be solved by method we studied in previous concepts.

(c) Integrals of the form

1. $\int \frac{p \cos x+q \sin x+r}{a \cos x+b \sin x+c} d x$
2. $\int \frac{p \cos x+q \sin x}{a \cos x+b \sin x} d x$

Working Rule:

Express numerator as $\lambda($ denominator $)+\mu($ differentiation of denominator $)+\gamma$

$\Rightarrow(\mathrm{p} \cos \mathrm{x}+\mathrm{q} \sin \mathrm{x}+\mathrm{r})=\lambda(\mathrm{a} \cos \mathrm{x}+\mathrm{b} \sin \mathrm{x}+\mathrm{c})+\mu(-\mathrm{a} \sin \mathrm{x}+\mathrm{b} \cos x)+\gamma$

where $\lambda, \mu$, and \gamma are constants to be determined by comparing the coefficients of $\sin x, \cos \mathrm{x}$, and constant terms on both sides.

$\begin{aligned}
\int \frac{p \cos \mathrm{x}+\mathrm{q} \sin \mathrm{x}+\mathrm{r}}{a \cos \mathrm{x}+\mathrm{b} \sin \mathrm{x}+\mathrm{c}} \mathrm{dx}= & \int \frac{\lambda(\mathrm{a} \cos \mathrm{x}+\mathrm{b} \sin \mathrm{x}+\mathrm{c})+\mu(-\mathrm{a} \sin \mathrm{x}+\mathrm{b} \cos \mathrm{x})+\gamma}{\mathrm{a} \cos \mathrm{x}+\mathrm{b} \sin \mathrm{x}+\mathrm{c}} \mathrm{dx} \\
= & \lambda \int \frac{a \cos x+b \sin x+c}{a \cos x+b \sin x+c} d x+\mu \int \frac{-a \sin x+b \cos x}{a \cos x+b \sin x+c} d x \\
& \quad+\int \frac{\mu}{\mathrm{a} \cos \mathrm{x}+\mathrm{b} \sin \mathrm{x}+\mathrm{c}} \mathrm{dx} \\
= & \lambda x+\mu \ln |a \cos x+b \sin x+c|+\int \frac{\mu}{a \cos x+b \sin x+c} d x
\end{aligned}$

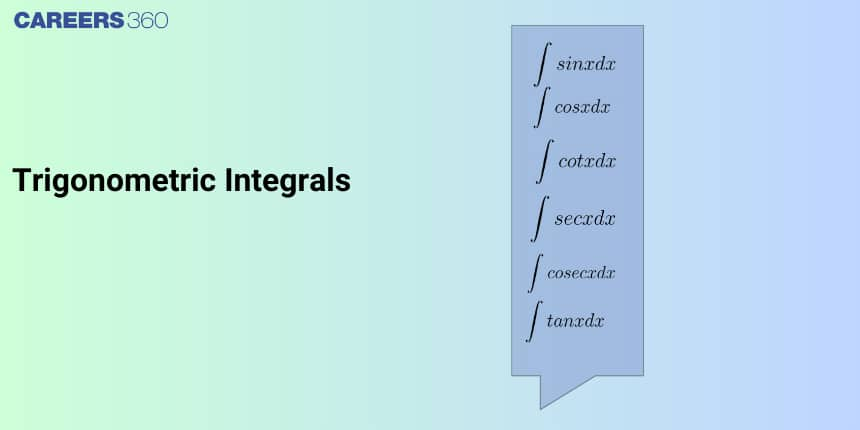
Recommended Video Based on Trigonometric Integrals

Solved Questions Based on Trigonometric Integrals

Example 1: Integrate $\int \frac{d x}{\sin ^2 x+2 \sin x \cos x}$

1) $\ln \frac{t+1}{t-1}+c$
2) $\ln \frac{t+2}{t}+c$
3) $\frac{1}{2} \ln \frac{t}{(t+2)}+C$
4) none of these

Solution
Divide by $\cos ^2 x$ in each case and pull $t=\tan x, d t=\sec ^2 x d x$

$\int \frac{d x \sec ^2 x}{\tan ^2 x+2 \tan x}=\int \frac{d t}{(t+1)^2-1}=\frac{1}{2} \ln \frac{t}{(t+2)}+C$

Hence, the answer is the option 3.
Example 2: $\int \frac{d x}{1+\sin x}$
1) $\frac{1}{1+\tan \left(\frac{x}{2}\right)}+C$

2) $-\frac{2}{\tan \left(\frac{x}{2}\right)+1}+C$
3) $\frac{1}{1+\cot \left(\frac{x}{2}\right)}+C$
4) $-\frac{1}{1+\cot \left(\frac{x}{2}\right)}+C$

$\begin{aligned}
& I=\int \frac{1}{\sin (x)+1} \mathrm{~d} x \\
& =\int \frac{\sec ^2\left(\frac{x}{2}\right)}{\left(\tan \left(\frac{x}{2}\right)+1\right)^2} \mathrm{~d} x \\
& \text { Put } u=\tan \left(\frac{x}{2}\right)+1 \Rightarrow \mathrm{d} x=\frac{2}{\sec ^2\left(\frac{x}{2}\right)} \mathrm{d} u \\
& I=2 \int \frac{1}{u^2} d u \\
& =-\frac{2}{u} \\
& =-\frac{2}{\tan \left(\frac{x}{2}\right)+1}+C
\end{aligned}$

Hence, the answer is the option (2).

Example 3: $\int \frac{d x}{3+4 \cos ^2 x}$ equals
1) $\frac{\sqrt{3}}{\sqrt{7}} \tan ^{-1}\left(\sqrt{\frac{3}{7}} \tan x\right)+C$
2) $\frac{1}{\sqrt{21}} \tan ^{-1}\left(\sqrt{\frac{3}{7}} \tan x\right)+C$

$\sqrt{3} \tan ^{-1}\left(\sqrt{\frac{3}{7}} \tan x\right)+C$

4) None of these

Solution
Divide numerator and denominator by $\cos ^2 x$

$\begin{aligned}
& \int \frac{\sec ^2 x d x}{3 \sec ^2 x+4} \\
& =\int \frac{\sec ^2 x d x}{3 \tan ^2 x+3+4} \\
& =\int \frac{\sec ^2 x d x}{7+3 \tan ^2 x}
\end{aligned}$

Put $\tan x=t \Rightarrow \sec ^2 x d x=d t$

$\begin{aligned}
& \int \frac{d t}{7+3 t^2} \\
& =\frac{1}{3} \int \frac{d t}{t^2+\left(\sqrt{\frac{7}{3}}\right)^2} \\
& =\frac{1}{3} \times \frac{\sqrt{3}}{\sqrt{7}} \tan ^{-1}\left(\sqrt{\frac{3}{7}} \tan x\right)+C \\
& =\frac{1}{\sqrt{21}} \tan ^{-1}\left(\sqrt{\frac{3}{7}} \tan x\right)+C
\end{aligned}$

Hence, the answer is the option 2.

Example 4: Integrate $\int \frac{d x}{\sin ^2 x+2 \cos ^2 x+2 \sin x \cos x}$
1) $x+c$
2) $\frac{1}{2} \tan ^{-1}(1+x)+C$
3) $\tan ^{-1}(1+\tan x)+C$

4) None of these

Solution

Divide by

$\begin{aligned}
& \int \frac{\sec ^2 x \cdot d x}{\tan ^2 x+2+2 \tan x} \\
& I=\int \frac{\sec ^2 x d x}{(\tan x+1)^2+1}
\end{aligned}$

Put $\tan (x)=t$

$\sec ^2 x d x=d t$

$\begin{aligned}
& I=\int \frac{d t}{(t+1)^2+1} \\
& =\tan ^{-1}(t+1)+C \\
& =\tan ^{-1}(\tan x+1)+C
\end{aligned}$

Hence, the answer is the option 3.
Example 5: $\int \frac{d x}{1+2 \cos x}$
1) $\frac{1}{\sqrt{3}} \ln \left|\frac{\sqrt{3}+\tan \frac{x}{2}}{\sqrt{3}-\tan \frac{x}{2}}\right|+c$
2) $-\frac{1}{\sqrt{3}} \cdot \ln \left|\frac{\tan \left(\frac{x}{2}\right)-\sqrt{3}}{\tan \left(\frac{x}{2}\right)+\sqrt{3}}\right|+c$
3) $\frac{2}{\sqrt{3}} \ln \left|\frac{\sqrt{3}+\tan \frac{x}{2}}{\sqrt{3}-\tan \frac{x}{2}}\right|+c$
4) None of these

4) None of these

Solution

$\begin{aligned} & \int \frac{d x}{1+2 \cos x} \\ & \int \frac{d x}{1+\frac{2-2 \tan ^2 \frac{x}{2}}{1+\tan ^2 \frac{2}{2}}} \\ & =\int \frac{\sec ^2\left(\frac{x}{2}\right) \cdot d x}{3-\tan ^2\left(\frac{x}{2}\right)} \\ & \text { Put } u=\tan \left(\frac{x}{2}\right) \Rightarrow \frac{1}{2} \sec ^2\left(\frac{x}{2}\right) \cdot d x=d u \\ & =-2 \int \frac{1}{u^2-3} d u \\ & =-\frac{1}{\sqrt{3}} \cdot \ln \left|\frac{u-\sqrt{3}}{u+\sqrt{3}}\right|+c \\ & =-\frac{1}{\sqrt{3}} \cdot \ln \left|\frac{\tan \left(\frac{x}{2}\right)-\sqrt{3}}{\tan \left(\frac{x}{2}\right)+\sqrt{3}}\right|+c\end{aligned}$Hence, the answer is the option (2).

Summary

Trigonometric integral is an important concept used in practical and traditional approaches in mathematics. Trigonometric integrals are integrals that involve trigonometric functions such as sine, cosine, tangent, and their inverses.

FAQs:

1) What is integration?

Solution: Integration is the reverse process of differentiation.

2) What is the other name of integration?

Solution: The other name of integration is antiderivative.

3) What is the integration of sin x?

Solution: An integration of sin x is -cos x.

4) What is an integration of cos x?

Solution: An integration of cos x is sin x.

5) What is an integration of sec x tanx?

Solution: an integration of sec x tan x is sec x.