Trigonometric Ratios - Definition, Formulas and Examples

Trigonometric ratios in mathematics are some fundamental concepts which helps us understand about the study of right-angled triangles, its sides, angles. Trigonometric ratios help in solving problems related to Physics, geometry, etc.

We will learn more about the trigonometric ratios in this article. It is an important concept as it comes directly as well as is mixed with some other concepts such as differential equation, integration, etc. It is crucial for both board level and competitive exams such as BITSAT, JEE Main, WBJEE, etc.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. Sides and angles of a Right angled Triangle
2. What is Trigonometric Ratio?
3. Trigonometric Ratios Formula
4. Relation between trigonometric Ratios
5. Trigonometric Ratio Table
6. Trigonometric Ratios for Complementary Angles
7. Application of Trigonometric Ratios in Height and Distance:
8. Important points

Sides and angles of a Right angled Triangle

The right angle triangle is a triangle in which one angle is 90 degrees.

Consider the triangle ABC, given above.

Base: If we wish to take trigonometric ratios of angle B, then the base is BC. It is the side on which the right-angle triangle stands.

Perpendicular (Altitude): Side opposite to the angle for which we want to find the trigonometric ratio.
In this case, AB is the altitude.
BC and AB are perpendicular to each other.

Hypotenuse: The side opposite to the right angle is called the hypotenuse. It is the largest side of the triangle. Side AC is the hypotenuse.

Relation between the sides of a right angles triangle: Pythagoras's theorem

Statement:

The square of the hypotenuse is equal to the sum of the square of the base and the square of the altitude.

$(Hypotenuse)^2= (Base)^2 + (Altitude)^2$

Pythagorean Triplets:

The three numbers which satisfy the above equation are known as the Pythagorean triplets.

For example, $(3, 4, 5)$ is a Pythagorean triplet because we know that $3^2= 9, 4^2 = 16$, and $5^2 = 25$ and, $9 + 16 = 25$.

Therefore, $3^2+4^2=5^2$.

Any three numbers that satisfy this condition are called Pythagorean triplets like $3, 4$, and $5$.

Some of the other examples of Pythagorean triplets are $(6, 8, 10)$, and $(12, 5, 13)$.

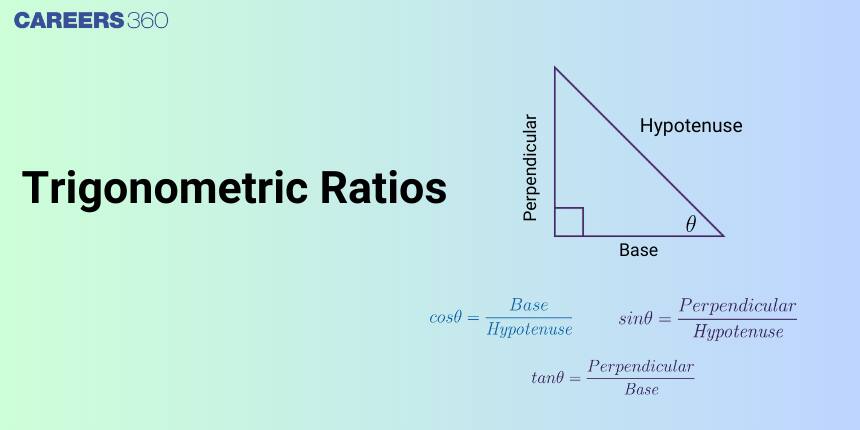
What is Trigonometric Ratio?

Trigonometric ratios are used to determine the ratios of any two sides out of the three sides of a right-angled triangle in terms of the respective angles.

The values of these trigonometric ratios can be calculated using the measure of an acute angle, $\theta$ in the right-angled triangle given below.

In trigonometry, there are six basic trigonometric ratios i.e., sin, cos, tan, sec, cosec(or csc), and cot in short. Below listed are trigonometric ratio formula:

sinθ: It is the short form of “sine”. In the above triangle, for the angle θ, $sin\theta = \frac{AC}{AB}$

cosθ: It is the short form of “cosine”. In the above triangle, for the angle θ,$cos\theta = \frac{BC}{AB}$

tanθ: It is the short form of “tangent”. In the above triangle, for the angle θ, $tan\theta = \frac{AC}{BC}$

cosecθ: It is the short form of “cosecant”. In the above triangle, for the angle θ, $cosec\theta = \frac{AB}{AC}$

secθ: It is the short form of “secant”. In the above triangle, for the angle θ, $sec\theta = \frac{AB}{BC}$

cotθ: It is the short form of “cotangent”. In the above triangle, for the angle θ, $cot\theta = \frac{BC}{AC}$

Trigonometric Ratios Formula

We use the short form of trigonometric ratio to compare the length of any two sides with the angle in the base. The angle $\theta$ is an acute angle $(θ < 90º)$ and in general is measured with reference to the positive $x$-axis, in the anticlockwise direction.

Here is the table of trigonometric ratios:

We can use some of the famous mnemonics to remember the main three sinθ, cosθ, and tanθ.

For sinθ, we will remember “Some People Have” [S = sinθ, P = Perpendicular, H = Hypotenuse]

For cosθ, we will remember “Curly Black Hair” [C = cosθ, B = Base, H = Hypotenuse]

For tanθ, we will remember “Through Proper Brushing” [T = tanθ, P = Perpendicular, B = Base]

Sometimes choosing the perpendicular side can be tough. It depends on the angle.

In the above triangle ABC,

For $∠CBA$, $sin\theta = \frac{AC}{BC}$

i.e., Here $AC$ is the perpendicular.

For $∠ACB$, $sin\theta’ = \frac{AB}{BC}$,

i.e., Here $AB$ is the perpendicular.

For this, we have to remember the adjacent side and opposite side.

Perpendicular = Opposite side of the angle considered

Base = Adjacent side of the angle considered

Hypotenuse will be the same in every case.

Relation between trigonometric Ratios

As we observe that sinθ is a reciprocal of cosecθ, cosθ is a reciprocal of secθ, tanθ is a reciprocal of cotθ, and vice-versa.

So, we can say

$ \sin \theta = \frac{1}{\csc \theta}$

$ \cos \theta = \frac{1}{\sec \theta}$

$\tan \theta = \frac{1}{\cot \theta}$

$ \csc \theta = \frac{1}{\sin \theta} $

$ \sec \theta = \frac{1}{\cos \theta}$

$\cot \theta = \frac{1}{\tan \theta}$

Trigonometric Ratio Table

In trigonometry, we use the values of trigonometric ratios for some standard angles i.e. 0°, 30°, 45°, 60°, and 90º.

Here is a trigonometric ratio chart which covers the basic trigonometric ratio class 10, listed below the trigonometric ratio values:

Trigonometric Ratios for Complementary Angles

The complementary angles are a pair of two angles such that their sum is equal to 90°. The complement of an angle $\theta$ is $90° - \theta$. The trigonometric ratios of complementary angles are:

$\sin(90^\circ - \theta) = \cos \theta$

$ \cos(90^\circ - \theta) = \sin \theta $

$ \csc(90^\circ - \theta) = \sec \theta $

$ \sec(90^\circ - \theta) = \csc \theta $

$ \tan(90^\circ - \theta) = \cot \theta $

$\cot(90^\circ - \theta) = \tan \theta$

We can see from above that sine and cosine are complementary to each other, cosecant and secant are complementary to each other, and tangent and cotangent are complementary to each other.

Application of Trigonometric Ratios in Height and Distance:

Trigonometry is one of the most important branches of mathematics. Some of the applications of trigonometry are:

• Measuring the heights of towers or big mountains
• Determining the distance of the shore from the sea
• Finding the distance between two celestial bodies
• Determining the power output of solar cell panels at different inclinations
• Representing different physical quantities such as mechanical waves, electromagnetic waves, etc.

Angle of Elevation and Angle of Depression:

The angle of Elevation:

When you see an object above you, there's an angle between the horizontal and your line of sight to the object.

Angle of Depression:

When you see an object below you, there's an angle between the horizontal and your line of sight to the object.

How to calculate the angle of elevation and angle of depression?

There are a few steps involved in calculating the angle of elevation and angle of depression.

Those steps are:

Step 1: Let the observer be at point A and the object is at point B.

Let the horizontal distance from A to the point directly below B on the horizontal line be d.

For the angle of elevation, the vertical distance from the horizontal line up to B is h.

For the angle of depression, the vertical distance from A down to the horizontal line is h.

Step 2: Use the tangent function.

We know, tanθ = $\frac{\text{Perpendicular}}{\text{Base}}$ = $\frac{h}{d}$,

Where θ is the angle of elevation or depression

Step 3: Calculate the angle.

$θ = tan^{-1} \frac{h}{d}$

Example:

From the top of an upright pole $24 \sqrt{3}$ feet high, the angle of elevation of the top of an upright tower was $60^{\circ}$. If the foot of the pole was 60 feet away from the foot of the tower, how tall (in feet) was the tower?

Here, AB = $24\sqrt3 ft = PQ$

Distance, $AP = 60$ feet

Here, $AP = BQ = 60$ feet

In $\triangle BQR$,

$\tan 60° = \frac{RQ}{BQ}$

⇒ $\sqrt3=\frac{RQ}{60}$

therefore $RQ = 60\sqrt3$

Height of the tower $= RP = RQ + PQ = 60\sqrt3+24\sqrt3=84\sqrt3$ feet

Hence, the correct answer is $84\sqrt3$ feet.

Important points

$\sin \theta = \frac{\text{Perpendicular}}{\text{Hypotenuse}} $

$ \cos \theta = \frac{\text{Base}}{\text{Hypotenuse}} $

$ \tan \theta = \frac{\text{Perpendicular}}{\text{Base}}$

$ \csc \theta = \frac{\text{Hypotenuse}}{\text{Perpendicular}} $

$\sec \theta = \frac{\text{Hypotenuse}}{\text{Base}}$

$ \cot \theta = \frac{\text{Base}}{\text{Perpendicular}}$

• In the angle of elevation and depression questions, we generally use $tan \theta$.

Practice Questions

Q1. In $\triangle{XYZ}$, right-angled at $Y$, if $\sin X = \frac{1}{2}$, find the value of $\cos X \cos Z + \sin X \sin Z$.

1. $\frac{\sqrt{3}}{2}$
2. $\frac{\sqrt{3}}{4}$
3. $\frac{2}{\sqrt{3}}$
4. $\sqrt{3}$

Hint: The sum of all angles in a triangle is 180°. Use this to find the value of $\cos X \cos Z + \sin X \sin Z$.

Answer:

Given: In $\triangle {XYZ}$, right-angled at $Y$.

We know that the sum of all the angles in a triangle is 180°.

$\sin X = \frac{1}{2}$

⇒ $\sin X = \sin{30°}$

So, $\angle X = 30°$

Then $\angle Z = 60°$, because $\angle Y + \angle X + \angle Z = 180°$

Then, $\cos X \cos Z + \sin X \sin Z$

$=\cos 30° \cos 60° + \sin 30° \sin 60°$

$=\frac{\sqrt{3}}{2} × \frac{1}{2} + \frac{1}{2} × \frac{\sqrt{3}}{2}$

$ = \frac{\sqrt{3}}{2}$

Hence, the correct answer is $\frac{\sqrt{3}}{2}$.

Q2. The angle of elevation of the top of a building at a distance of 70 m from its foot on a horizontal plane is found to be 60°. Find the height of the building.

1. $70 \sqrt{3} \mathrm{~m}$
2. $60 \sqrt{3} \mathrm{~m}$
3. $50 \sqrt{3} \mathrm{~m}$
4. $70 \sqrt{2} \mathrm{~m}$

Hint: Use formula, $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$

Answer:

Height = AC

We know, $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$

⇒ $\tan60° =\frac{AC}{70}$

⇒ $\sqrt3=\frac{AC}{70}$

⇒ $AC=70\sqrt3\text{ m}$

Hence, the correct answer is $70\sqrt3\text{ m}$.

Q3. If $2 \cot \theta = 3$, find the value of $\frac{\sqrt{13} \sin \theta – 3 \tan \theta}{3 \tan \theta + \sqrt{13} \cos \theta}$

1. $\frac{1}{\sqrt{13}}$
2. $\frac{2}{\sqrt{13}}$
3. 0
4. $\frac{2}{3}$

Hint: $\cot \theta=\frac{\text{Base}}{\text{Perpendicular}} =\frac{3}{2}$, then use Pythagoras's theorem to find the hypotenuse.

Answer:

$2 \cot \theta = 3$

$⇒\cot \theta=\frac{3}{2}$

$⇒\frac{\text{Base}}{\text{Perpendicular}} =\frac{3}{2}$

$⇒\frac{AB}{BC}= \frac{3}{2}$

Let $AB = 3k, BC = 2k$

From Pythagoras' Theorem,

$AC^{2} = AB^{2} + BC^{2}$

$⇒AC^{2} = (3k)^{2} + (2k)^{2}$

$⇒AC^{2} = 13k^2$

$⇒AC = \sqrt{13}k$

$\sin\theta = \frac{\text{Perpendicular}}{\text{Hypotenuse}} = \frac{2k}{\sqrt{13}k}=\frac{2}{\sqrt{13}}$

$\cos\theta = \frac{\text{Base}}{\text{Hypotenuse}} = \frac{3k}{\sqrt{13}k}= \frac{3}{\sqrt{13}}$

$\tan \theta = \frac{\text{Perpendicular}}{\text{Base}} = \frac{2k}{3k}=\frac{2}{3}$

Putting these values in the equation, we get,

$=\frac{\sqrt{13} \sin \theta – 3 \tan \theta}{3 \tan \theta + \sqrt{13} \cos \theta}$

$=\frac{\sqrt{13} \times \frac{2}{\sqrt{13}} - 3 \times \frac{2}{3}}{3 \times\frac{2}{3} + \sqrt{13} \times \frac{3}{\sqrt{13}}}$

$=0$

Hence, the correct answer is 0.

Q4. Subhas, a 3.15 m tall tree, and an 11.25 m tall building are positioned such that their feet on the ground are collinear and the tree is located between Subhas and the building. The tree is located at a distance of 7.5 m from Subhas and a distance of 45 m from the building. Further, the eyes of Subhas, the top of the tree, and the top of the building fall in one line. Find the height (in m ) from the ground at which Subhas's eyes are situated.

1. 1.75
2. 1.6
3. 1.8
4. 1.5

Hint: Assume the required height as $h$. Draw a figure according to the given data. Solve for $h$ using the trigonometric ratios.

Answer:

Let XA be Subhas, YB be the tree, and ZC be the building.

YB = 3.15 m

ZC = 11.25 m

AB = 7.5 m

BC = 45 m

XO = AB = 7.5 m

OP = BC = 45 m

⇒ XP = XO + OP = 7.5 + 45 = 52.5 m

Let the height from the ground at which Subhas's eyes are situated be $h$.

OY = BY – OB = 3.15 – $h$

PZ = ZC – PC = 11.25 – $h$

Let the angle of elevation be $\theta$.

In $\triangle$XPZ, $\tan \theta = \frac{\text{PZ}}{\text{PX}} = \frac{11.25-h}{52.5}$ -----------(i)

In $\triangle$XOY, $\tan \theta = \frac{\text{OY}}{\text{OX}} = \frac{3.15-h}{7.5}$ ------------(ii)

$⇒ \frac{11.25-h}{52.5} = \frac{3.15-h}{7.5}$

$⇒ \frac{11.25-h}{7} = \frac{3.15-h}{1}$

$⇒11.25-h = 7(3.15-h)$

$⇒11.25-h = 22.05-7h$

$⇒6h = 10.8$

$\therefore h = \frac{10.8}{6} = 1.8$ m

Hence, the correct answer is 1.8.

Q5. If $\triangle A B C$ is right angled at $B, A B=12 \mathrm{~cm}$ and $\angle C A B=60^{\circ}$, determine the length of $BC$.

1. $24 \sqrt{3} \mathrm{~cm}$
2. $12 \mathrm{~cm}$
3. $12 \sqrt{2} \mathrm{~cm}$
4. $12 \sqrt{3} \mathrm{~cm}$

Hint: Use the trigonometric ratio involving AB and BC.

Answer:

Given, $\triangle$ABC is right angled at B, where AB = 12 cm and $\angle$CAB = 60°

By using the trigonometric ratio involving AB and BC.

To $\angle$CAB, AB is the adjacent side and BC is the opposite side.

$\tan\angle CAB$ = $\tan 60°$ = $\frac{BC}{AB}$

⇒ $\sqrt3=\frac{BC}{12}$

$\therefore BC =12\sqrt3\ \text{cm}$

Hence, the correct answer is $12\sqrt3\ \text{cm}$.

Q6. From the top of an upright pole 17.75 m high, the angle of elevation of the top of an upright tower was 60°. If the tower was 57.75 m tall, how far away (in m) from the foot of the pole was the foot of the tower?

1. $40 \sqrt{3}$
2. $\frac{151 \sqrt{3}}{6}$
3. $\frac{77}{4} \sqrt{3}$
4. $\frac{40 \sqrt{3}}{3}$

Hint: Use $\tan\theta=\frac{\text{Perpendicular}}{\text{Base}}$

Answer:

We have to find the value of $x$.

In $\triangle ABC,$

$\tan60° = \frac{AC}{BC}$

We know, $CE=BD$

⇒ $AC=AE-CE$

⇒ $AC=57.75-17.75$

⇒ $AC=40$

In $\triangle ABC,$

$\tan60° = \frac{40}{x}$

⇒ $\sqrt3=\frac{40}{x}$

⇒ $x=\frac{40}{\sqrt3}$

⇒ $x=\frac{40\sqrt3}{3}$ m

Hence, the correct answer is $\frac{40\sqrt3}{3}$.

Q7. The value of $(\sin^445°+ \cos^460°) + (\tan^445°+ \cot^445°)$ is:

1. $\frac{37}{16}$
2. $\frac{33}{16}$
3. $\frac{35}{16}$
4. $\frac{39}{16}$

Hint: $\sin45°=\frac{1}{\sqrt2},\cos60°=\frac{1}{2},\tan45°=1$ and $\cot45°=1$

Answer:

Given: $(\sin^445°+ \cos^460°) + (\tan^445°+ \cot^445°)$

= $(\frac{1}{\sqrt2})^4 + (\frac{1}{2})^4 + (1)^4 + (1)^4$

= $\frac{1}{4} + \frac{1}{16} + 1 + 1$

= $\frac{4+1+16+16}{16}$

= $\frac{37}{16}$

Hence, the correct answer is $\frac{37}{16}$.

Q8. Two ships are on the opposite of a lighthouse such that all three of them are collinear. The angles of depression of the two ships from the top of the lighthouse are 30° and 60°. If the ships are $230 \sqrt{3}$ m apart, then find the height of the lighthouse (in m).

1. 175.4
2. 165.2
3. 172.5
4. 180.5

Hint: Use the formula: $\tan\theta=\frac{\text{Perpendicular}}{\text{Base}}$

Answer:

Given: The distance between the ships is BC = $230\sqrt3$ m

Let the height of the lighthouse AD be $h$ m.

From $\triangle$ABD we get,

$\tan30°=\frac{AD}{BD}$ ⇒ BD = $h\sqrt3$

Again from $\triangle$ACD we get,

$\tan60°=\frac{AD}{CD}$ ⇒ CD = $\frac{h}{\sqrt3}$

According to the question,

$h\sqrt3+\frac{h}{\sqrt3}=230\sqrt3$

⇒ $3h+h=690$

⇒ $4h=690$

⇒ $h=\frac{690}{4}=172.5$ m

Hence, the correct answer is 172.5 m.

Q9. If $\tan (A+B)=\sqrt{3}$ and $\tan (A-B)=\frac{1}{\sqrt{3}}; 0°<(A+B)<90°; A > B$, then the values of $A$ and $B$ are respectively:

1. 45° and 15°
2. 15° and 45°
3. 30° and 30°
4. 60° and 30°

Hint: $\sqrt{3}=\tan60°$ and $\frac{1}{\sqrt{3}}=\tan30°$

Answer:

Given: $\tan (A+B)=\sqrt{3}$ and $\tan (A-B)=\frac{1}{\sqrt{3}}$

$\tan (A+B)=\sqrt{3}=\tan60°$

⇒ $A+B=60°$ .........................(1)

Also, $\tan (A-B)=\frac{1}{\sqrt{3}}=\tan30°$

⇒ $A-B=30°$ ............................(2)

Solving equations (1) and (2) we get,

$A=45°$ and $B=15°$

Hence, the correct answer is 45° and 15°.

Q10. A person 1.8 metres tall is $30 \sqrt{3}$ metres away from a tower. If the angle of elevation from his eye to the top of the tower is 30°, then what is the height (in m) of the tower?

1. 32.5
2. 37.8
3. 30.5
4. 31.8

Hint: Find the height of the tower using the formulas, $\tan 30^{\circ}=\frac{1}{\sqrt3}$ and $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$.

Answer:

Given: A person 1.8 metres tall is $30 \sqrt{3}$ metres away from a tower.

The angle of elevation from his eye to the top of the tower is $30^{\circ}$.

We know the formulas, $\tan 30^{\circ}=\frac{1}{\sqrt3}$ and $\tan \theta=\frac{\text{Perpendicular}}{\text{Base}}$.

Let the tower's height and the person's height be AB and DE, respectively.

In $\triangle ACD$,

$\frac{AC}{DC}=\tan 30^{\circ}$

⇒ $\frac{x}{30\sqrt3}=\frac{1}{\sqrt3}$

⇒ $x=30$ m

The height of the tower AB = 30 + 1.8 = 31.8 m

Hence, the correct answer is 31.8 m.