Universal set

Universal set Definition

A set that contains all the elements or objects of other related sets, including its own elements, is called the Universal Set. The symbol of the universal set is usually denoted by $U$, and all its subsets are denoted by the letters $\mathrm{A}, \mathrm{B}, \mathrm{C}$, etc.

Universal set example, for the set of all integers, the universal set can be the set of rational numbers or, for that matter, the set $R$ of real numbers.

Let's look at a universal set example in real life.

If $A$ is a set of all tigers in a jungle, and $B$ is a set of all deer in the jungle, then the universal set can be all the animals of that jungle, as all tigers and all deer are subsets of this set.

Similarly, if $A$ is a set of all roses and $B$ is a set of all tulips, then the universal set could be the set of all flowers in the world, where the sets $A$ and $B$ are the subsets of the universal set.

This basic set is called the "Universal Set".

All the sets under consideration are likely to be subsets of a set called the universal set, which is denoted by $\Omega$ or $S$ or $U$.

Example: The set of all letters in the alphabet of the English language $U = \{a,b,c,.......,x,y,z\}$ is the universal set of vowels in the alphabet of the English language. i.e. $A=\{a,e,i,o,u\}$

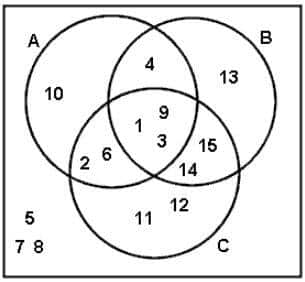
Venn Diagram of Universal Set

Let $U = \{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15\}$ and $A = \{10,4,2,6,1,9,3\}$, $B=\{4,13,1,9,3,15,14\}$ and $C =\{2,6,1,9,3,14,15,11,12\}$.

The Venn diagram to represent the universal set and its subsets of the above example is

Properties of the Universal Set

1. When we take a union from a universal set then the result will be the universal set. $U \cup A=U$

Note: If $A$ is a subset of $B$, then $A \cup B=B$
2. The universal set contains all elements under consideration

Complement of Universal Set

Let $U$ be the universal set and $A$ be a subset of $U$. Then the complement of $A$ is the set of all elements of $U$ which are not the elements of $A$.

Complement of set $A$ is denoted by $A^\prime$ or $A^C$

$A^{\prime}=\{x: x \in U \text { and } x \notin A\} \text {. Obviously, } A^{\prime}=U-A$
The complement of the universal set is the empty set, i.e, $U^{\prime}=\phi$

Cardinality of Universal Set

The cardinality of a universal set refers to the total number of distinct elements it contains. If $U$ is a finite set, the cardinality is denoted by $n(U)$ or $|U|$.
For example, if:

$U = \{1, 2, 3, 4, 5\}, \quad \text{then } |U| = 5$

In the case of an infinite universal set, such as:

$U = \mathbb{N} = \{1, 2, 3, \ldots\}$

the cardinality is infinite. Understanding the size and count of elements in the universal set is crucial in areas like probability, logic, and combinatorics.

Universal Set and Union of Sets

The universal set is the union of all its subsets together with some more elements in some cases. Now, let us look at an example. Consider three sets with elements set $A = \{a, b, c\}$ and set $B = \{e, f, g\}$. Let's find all the possible universal sets for the sets $A$ and $B$.

• The universal set of the above two sets can be the set of all letters $\{a, b, c, d, …, z\}$
• The union between $A$ and $B$ is given as: $A ∪ B = \{a, b, c, e, f, g\}$

Thus, we can see that the universal set contains the elements from $A, B,$ and $U$ itself, whereas the union of $A$ and $B$ contains elements from only $A$ and $B$.

Relationship with Subsets and Complement

Every set being considered in a given problem is a subset of the universal set. Furthermore, the complement of any set is defined with respect to the universal set. For example, if:

• $U = \{a, b, c, d\}$
• $A = \{a, b\}$

Then the complement of $A$ is:

$A' = U - A = \{c, d\}$

This shows the importance of the universal set in defining set complements, and helps in operations like De Morgan's Laws and logical negation.

Examples of Universal Set

Seeing examples of a universal set in different contexts makes it easier to understand how it functions in set theory. This section provides clear numerical, alphabetical, and real-life examples to illustrate the use and structure of universal sets.

Universal Set Example in Numbers

Let’s consider a common scenario involving numbers. Suppose we're working with sets that contain natural numbers less than 10. Then the universal set of natural numbers under consideration would be:

$U = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}$

Now if we define a subset $A = \{2, 4, 6\}$, it is clear that $A \subseteq U$.
This example shows how a universal set in number theory can be used as a reference set for all subsets in a particular context.

Universal Set Example in Alphabets or Objects

Consider a classroom with students having the first letters of their names. The universal set of alphabets could be:

$U = \{\text{A, B, C, D, E, F, G}\}$

If we define $B = \{\text{A, D, F}\}$ as a set of students in Group B, then $B$ is clearly a subset of $U$.
This illustrates how universal sets with letters or real-world objects help define the scope of a problem or group.

Real-Life Examples of Universal Set in Daily Use

In real life, suppose a supermarket is tracking items sold in a week. The universal set of items sold could be:

$U = \{\text{Milk, Bread, Eggs, Rice, Oil, Sugar}\}$

A subset could be items bought on Monday:

$M = \{\text{Milk, Rice, Sugar}\}$

This practical example of a universal set in daily life shows how all subsets operate within a defined complete group, making universal sets essential in data categorisation and management.

Universal Set and Set Operations

The universal set plays a central role in various set operations such as union, intersection, and complement. These operations help define relationships between sets within a defined universal context. This section explains how the universal set interacts with other sets through fundamental operations.

Union with Universal Set

The union of any set with the universal set always returns the universal set itself:

$A \cup U = U$

This is because all elements of $A$ are already included in $U$.
For example, if $A = \{1, 2\}$ and $U = \{1, 2, 3, 4\}$, then:

$A \cup U = \{1, 2, 3, 4\} = U$

This property is fundamental in set operations involving the universal set.

Intersection with Universal Set

The intersection of any set with the universal set returns the set itself:

$A \cap U = A$

This is because $U$ contains all possible elements under consideration. For example:
If $A = \{x, y\}$ and $U = \{x, y, z\}$, then:

$A \cap U = \{x, y\} = A$

This rule is frequently used in problems involving Venn diagrams and set identities.

Complement Relative to Universal Set

The complement of a set $A$ is defined as all elements in the universal set $U$ that are not in $A$:

$A' = U - A$

If $U = \{a, b, c, d\}$ and $A = \{a, d\}$, then:

$A' = \{b, c\}$

This is a key concept in understanding De Morgan's Laws, set subtraction, and complementary events in probability.

Universal Set vs Other Types of Sets

Understanding how the universal set compares to other types of sets helps clarify its unique role in set theory. This section highlights the key differences between the universal set and subsets, empty sets, and both finite and infinite sets.

Difference Between Universal Set and Subset

A universal set contains all elements under discussion, while a subset includes some or all of those elements.
If $U = \{1, 2, 3, 4\}$ and $A = \{2, 3\}$, then clearly:

$A \subseteq U \quad \text{but} \quad U \not\subseteq A$

This comparison highlights the hierarchical relationship between a universal set and its subsets.

Difference Between Universal Set and Empty Set

The empty set (or null set) contains no elements:

$\emptyset = \{\}$

On the other hand, the universal set contains all possible elements under the context.
For instance, if $U = \{a, b, c\}$, then:

$\emptyset \subseteq U \quad \text{but} \quad \emptyset \ne U$

This shows the extreme contrast between the null set and the universal set in terms of cardinality and content.

Comparison with Finite and Infinite Sets

A universal set can be either finite or infinite, depending on the context.

• Finite example: $U = \{1, 2, 3, 4, 5\}$
• Infinite example: $U = \{1, 2, 3, 4, \ldots\}$
  In contrast, a finite set contains a countable number of elements, while an infinite set goes on endlessly.
  Thus, the universal set may overlap with or include both finite and infinite sets, depending on how it is defined.

Solved Examples Based On the Universal Set

Example 1: If $A$ is any set, then which of the following is not a property of a Universal Set?
1) $A \cup A^c=U$
2) $A \cap A^c=U$
3) $U-A=A^c$
4) $U-A^c=A$

Solution
There is no common portion between $A$ and $A^{\prime}$,
$A\cap A^{c}=\phi$. So $(2)$ is wrong.
Hence, the answer is option 2.

Example 2: If $\mathrm{G}=\{-9,-8,-7,-6\}$ and $\{8,2,7,4\}$, then which of the following MAY BE a universal set?
1) Set of all whole numbers
2) Set of all irrational numbers
3) Set of all integers
4) All of the above

Solution
We know the elements of both sets $G$ and $H$ are there in the set of all integers, hence option (3) can be a universal set.
Hence, the answer is option 3.

Example 3: If $U=\{a, b, c, d, e, f, h, i, j\}$ which of the following is not a subset of $U$ ?
1) $\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$
2) \{c.d.g\}
3) $\{\mathrm{h}, \mathrm{b}, \mathrm{j}\}$
4) $\{\mathrm{a}, \mathrm{i}, \mathrm{d}\}$

Solution
As we learnt
A set that contains all sets in a given context is called the "Universal Set". The universal set is usually denoted by $U$, and all its subsets by the letters $A, B, C$, etc.
wherein
R is the universal set of $\mathrm{N}, \mathrm{W}$ and Z .
Set U has no element ' g ' in it.
Hence, the answer is option 2.

Example 4: If $\mathrm{n}(\mathrm{U})=100, \mathrm{n}(\mathrm{A})=30, \mathrm{n}(\mathrm{B})=40$ and $n(A \cap B)=10$. Find $n\left(A^c \cap B^c\right)$
1) 30
2) 40
3) 50
4) 60

Solution
$\begin{aligned} & n(A \cup B)=n(A)+n(B)-n(A \cap B) \\ & n(A \cup B)=30+40-10=60 \\ & n(A \cup B)^{\prime}=n\left(A^{\prime} \cap B^{\prime}\right)=n(U)-n(A \cap B) \\ & =100-60=40\end{aligned}$
Hence, the answer is option 2.

Example 5: The set which contains those elements of the Universal set which are not contained in set $A$ is called the complement of set $A$. (True/False)

Solution
Complement of a Set:
If $U$ is a universal set and $A$ is a subset of $U$, then the complement of $A$ is the set which contains those elements of $U$ which are not contained in $A$. Symbolically, we write $A′$ to denote the complement of $A$ with respect to $U$.
The statement is true.

List of Topics Related to Universal Set

To understand the concept of a universal set thoroughly, it is helpful to explore the related foundational topics in set theory. These concepts support the definition, application, and operations involving universal sets. This section lists all key topics connected to universal sets.

NCERT Resources

Explore essential NCERT study materials for Sets, with comprehensive solutions, concise revision notes, and curated exemplar problems. These resources are designed to enhance your conceptual clarity and prepare you effectively for board and competitive exams.

NCERT Solutions for Class 11 Chapter 1 Sets

NCERT Notes for Class 11 Chapter 1 Sets

NCERT Exemplar for Class 11 Chapter 1 Sets

Practice Questions

Mastering any mathematical concept comes through continuous practice. To help strengthen your understanding of the topic, we have given below some practice questions that will test your knowledge of formulas, important properties and general application of knowledge.