Addition of Vectors and Subtraction of Vectors

Each vector may have its own direction, the process of addition of vectors is different from adding two scalars. There are many laws by which we can add two vectors i.e. Triangular law of addition, Polygon law of addition, and the parallelogram of addition. In real life, we use vectors for tracking objects that are in motion, and localization of places and things.

JEE Main 2025: Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

JEE Main 2025: Maths Formulas  | Study Materials

JEE Main 2025: Syllabus | Preparation Guide | High Scoring Topics 

This Story also Contains

1. What is Vector Quantity?
2. What is Vector Addition?
3. Condition of Vector Addition
4. Laws of Vector Addition
5. Triangular Law of addition
6. Parallelogram Law of Addition
7. Polygon law of addition
8. Subtraction of Vectors
9. Solved Examples Based on Vector Addition and Subtraction
10. Summary

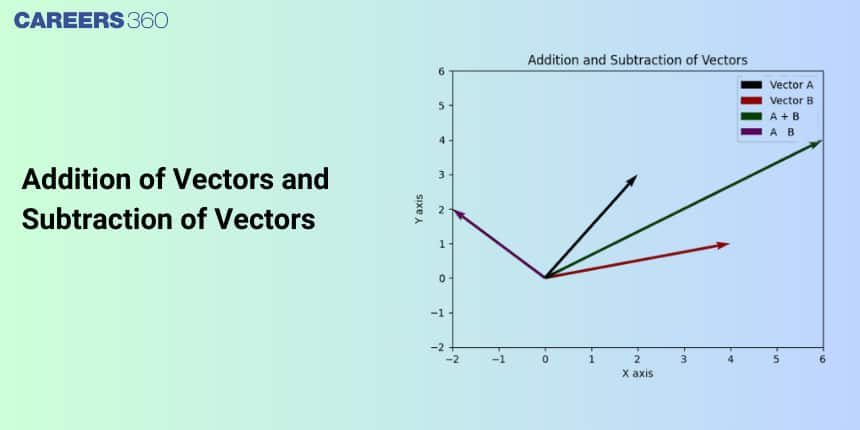
In this article, we will cover the concept of Vector Addition and Subtraction. This topic falls under the broader category of Vector Algebra, which is a crucial chapter in Class 11 Mathematics. This is very important not only for board exams but also for competitive exams, which even include the Joint Entrance Examination Main and other entrance exams: SRM Joint Engineering Entrance, BITSAT, WBJEE, and BCECE. A total of twelve questions have been asked on this topic in JEE Main from 2013 to 2023 including one in 2021, and two in 2023.

What is Vector Quantity?

A quantity that has magnitude as well as a direction in space and follows the triangle law of addition is called a vector quantity, e.g., velocity, force, displacement, etc.

We denote vectors by boldface letters, such as a or $\vec{a}$.

What is Vector Addition?

Vector addition is the operation in which two vectors are added to get their sum.

Since each vector may have its own direction, the process of addition of vectors is different from adding two scalars. The most common graphical method for adding two vectors is to place the initial point of the second vector at the terminal point of the first, as in Fig (a).

Suppose, for example, that both vectors represent displacement. If an object moves first from the initial point to the terminal point of vector$\overrightarrow{\mathbf{a}}$, then from the initial point to the terminal point of vector $\vec{b}$, the overall displacement is the same as if the object had made just one movement from the initial point of $\vec{a}$ to the terminal point of the vector $\vec{b}$. Thus $\vec{a}+\vec{b}$joins starting point of one vector to the terminal point of another vector when they are placed one after the other. For obvious reasons, this approach is called the triangle method

Condition of Vector Addition

• We cannot add vectors and scalars together.

• Vectors can be added only if they are of the same nature.

Laws of Vector Addition

There are three basic laws of vector addition that are used to add vectors

1) Triangular Law of addition

2) Parallelogram Law of Addition

3) Polygon law of addition

Triangular Law of addition

A vector AB simply means the displacement from point A to point B. Now consider a situation where a boy moves from A to B and then from B to C. The net displacement made by the boy from point A to point C is given by vector AC

This is known as the triangle law of vector addition. In general, if we have two vectors a and b, then to add them, they are positioned such that the initial point of one coincides with the terminal point of the other.

When the sides of the triangle are taken in order, it leads to zero resultant as the initial and terminal points get coincide.

Parallelogram Law of Addition

A second method for adding vectors is called the parallelogram method. With this method, we place the two vectors so they have the same initial point, and then we draw a parallelogram with the vectors as two adjacent sides, as in Fig (b) If we have two vectors a and b represented by the two adjacent sides of the parallelogram in magnitude and direction, then their sum a+b is represented in magnitude and direction by the diagonal of the parallelogram through their common point. This is known as the parallelogram law of vector addition.

Here the sum of the vectors is given by the vector along the diagonal that passes through the common starting point of both the vectors.

Polygon law of addition

If a number of vectors can be represented in magnitude and direction by the sides of a polygon taken in the same order, then their resultant is represented in magnitude and direction by the closing side of the polygon taken in the opposite order.

$
\vec{a}+\vec{b}+\vec{c}+\vec{d}+\vec{e}=-\vec{f}
$
OR,

$
\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DE}}+\overrightarrow{\mathrm{EF}}=\overrightarrow{\mathrm{AF}}
$

Subtraction of Vectors

If a and b are two vectors, then their subtraction, or differenc$\vec{a}-\vec{l}$ s defined as $\overrightarrow{\mathbf{a}}+(-\overrightarrow{\mathbf{b}})$, where $(-\overrightarrow{\mathbf{b}})$s the negative of vector b has equal magnitude but opposite direction that of b. Graphically, it is depicted by drawing a vector from the terminal point of b to the terminal point of a.

If the vectors are defined in terms of $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$, i.e.,
$\vec{a}=a_1 \hat{\mathbf{i}}+a_2 \hat{\mathbf{j}}+a_3 \hat{\mathbf{k}}$ and $\vec{b}=b_1 \hat{\mathbf{i}}+b_2 \hat{\mathbf{j}}+b_3 \hat{\mathbf{k}}$ then their sum is defined as,

$
\vec{a}+\vec{b}=\left(a_1+b_1\right) \hat{\mathbf{i}}+\left(a_2+b_2\right) \hat{\mathbf{j}}+\left(a_3+b_3\right) \hat{\mathbf{k}}
$
If,
$\vec{a}=a_1 \hat{\mathbf{i}}+a_2 \hat{\mathbf{j}}+a_3 \hat{\mathbf{k}}$ and $\vec{b}=b_1 \hat{\mathbf{i}}+b_2 \hat{\mathbf{j}}+b_3 \hat{\mathbf{k}}$ then their difference is defined as,

$
\vec{a}-\vec{b}=\left(a_1-b_1\right) \hat{\mathbf{i}}+\left(a_2-b_2\right) \hat{\mathbf{j}}+\left(a_3-b_3\right) \hat{\mathbf{k}}
$
Properties of vector addition
The sum of two vectors is always a vector.
1. $\vec{a}+\vec{b}=\vec{b}+\vec{a}$
(Commutative property)
2. $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$ (Associative property)
3. $\vec{a}+\overrightarrow{0}=\overrightarrow{0}+\vec{a}=\vec{a}$ (additive identity)
4. $\vec{a}+(-\vec{a})=(-\vec{a})+\vec{a}=\overrightarrow{0}$ (additive inverse)

Properties of vector Subtraction

1. $\vec{a}-\vec{b} \neq \vec{b}-\vec{a}$
2. $(\vec{a}-\vec{b})-\vec{c} \neq \vec{a}-(\vec{b}-\vec{c})$
3. For any two vectors $\vec{a}$ and $\vec{b}$
(a) $|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|$
(b) $|\vec{a}+\vec{b}| \geq|| \vec{a}|-| \vec{b} \mid$
(c) $|\vec{a}-\vec{b}| \leq|\vec{a}|+|\vec{b}|$
(d) $|\vec{a}-\vec{b}| \geq|| \vec{a}|-| \vec{b}||$

Recommended Video Based on Vector Addition and Subtraction

Solved Examples Based on Vector Addition and Subtraction

Example 1: An arc PQ of a circle subtends a right angle at its center O. The midpoint of the arc PQ is R. I$\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{u}}, \overrightarrow{\mathrm{OR}}=\overrightarrow{\mathrm{v}}$ and $\overrightarrow{\mathrm{OQ}}=\alpha \overrightarrow{\mathrm{u}}+\beta \overrightarrow{\mathrm{v}}$; then $\alpha, \beta^2$ are the roots of the equation : [JEE MAINS 2023]

Solution

Let $\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{u}}=\hat{\mathrm{i}}$
Let $\overrightarrow{O Q}=\vec{q}=\hat{j}$
$\because R$ is the midpoint of $\overrightarrow{P Q}$

Then

$
\overrightarrow{O R}=\vec{v}=\frac{1}{\sqrt{2}} \hat{i}+\frac{1}{\sqrt{2}} \hat{j}
$
Now

$
\begin{aligned}
& \overrightarrow{\mathrm{OQ}}=\alpha \overrightarrow{\mathrm{u}}+\beta \overrightarrow{\mathrm{v}} \\
& \hat{\mathrm{j}}=\alpha \hat{\mathrm{i}}+\beta\left(\frac{1}{\sqrt{2}} \hat{\mathrm{i}}+\frac{1}{\sqrt{2}} \hat{\mathrm{j}}\right) \\
& \beta=\sqrt{2}, \alpha+\frac{\beta}{\sqrt{2}}=0 \Rightarrow \alpha=-1
\end{aligned}
$
Now equation

$
\begin{aligned}
& x^2-\left(\alpha+\beta^2\right) x+\alpha \beta^2=0 \\
& x^2-(-1+2) x+(-1)(2)=0 \\
& x^2-x-2=0
\end{aligned}
$
Hence, the answer is $x^2-x-2=0$

Example 2: Let ABCD be a quadrilateral. If E and Fare the midpoints of the diagonals AC and BD respectively and $(\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{BC}})+(\overrightarrow{\mathrm{AD}}-\overrightarrow{\mathrm{DC}})=k \overrightarrow{\mathrm{FE}}$ then $k$ is equal to
[JEE MAINS 2023]

Solution

$\begin{aligned} & \overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{DC}}=\mathrm{k} \overrightarrow{\mathrm{FE}} \\ & (\vec{b}-\overrightarrow{\mathrm{a}})-(\overrightarrow{\mathrm{c}}-\overrightarrow{\mathrm{b}})+(\overrightarrow{\mathrm{d}}-\overrightarrow{\mathrm{a}})-(\overrightarrow{\mathrm{c}}-\overrightarrow{\mathrm{d}})=\mathrm{k} \overrightarrow{\mathrm{FE}} \\ & 2(\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{d}})-2(\overrightarrow{\mathrm{a}}-\overrightarrow{\mathrm{c}})=\mathrm{k} \overrightarrow{\mathrm{FE}} \\ & 2(2 \overrightarrow{\mathrm{f}})-2(2 \overrightarrow{\mathrm{e}})=\mathrm{kFE} \\ & 4(\overrightarrow{\mathrm{f}}-\overrightarrow{\mathrm{e}})=\mathrm{k} \overrightarrow{\mathrm{FE}} \\ & -4 \overrightarrow{\mathrm{FE}}=\mathrm{kFE} \\ & \mathrm{k}=-4\end{aligned}$

Hence, the answer is -4

Example 3: Let $\vec{a}, \vec{b}$ and $\vec{c}$ be three unit vectors such that $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}$. If $\lambda=\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}$ and $\vec{d}=\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}$, then the ordered pair is equal to:
[JEE MAINS 2020]

$
\begin{gathered}
|\vec{a}+\vec{b}+\vec{c}|^2=0 \\
3+2(\vec{a} \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a})=0 \\
(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a})=\frac{-3}{2}
\end{gathered}
$
Solution:

$
\begin{aligned}
& \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}=\overrightarrow{0} \\
& \vec{d}=\vec{a} \times \vec{b}+\vec{b} \times(-\vec{a}-\vec{b})+(-\vec{a}-\vec{b}) \times \vec{a} \\
& =\vec{a} \times \vec{b}+\vec{a} \times \vec{b}+\vec{a} \times \vec{b} \\
& \vec{d}=3(\vec{a} \times \vec{b})
\end{aligned}
$
Hence, the answer is $\left[-\frac{3}{2}, 3 \vec{a} \times \vec{b}\right]$

Example 4: If $\vec{a}, \vec{b}, \vec{c}_{\text {represents vectors }} \overrightarrow{A B}, \overrightarrow{B C}, \overrightarrow{C A}$ of a triangle then $\vec{a}+\vec{b}+\vec{c}$ equals:
Solution: Triangle law of addition -If two vectors are given by two consecutive sides of a triangle, then the closing side gives the sum of these two vectors.

$
\begin{aligned}
& \overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}=\vec{a}+\vec{b} \text { and } \overrightarrow{C A}=\vec{c} \\
& \Rightarrow \vec{a}+\vec{b}+\vec{c}=\overrightarrow{A C}+\overrightarrow{C A}=\overrightarrow{A C}-\overrightarrow{A C}=\overrightarrow{0}
\end{aligned}
$
Hence, the answer is $\overrightarrow{0}$
Example 5: Let OACB be a parallelogram, then $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$ equals
Solution: Parallelogram law of addition - If two vectors $\vec{a}$ and $\vec{b}$ are represented by $\overrightarrow{O A}$ and $\overrightarrow{O B}$, then their sum $\vec{a}+\vec{b}$ is represented by $\overrightarrow{O C}$, the diagonal of the parallelogram OACB

$\begin{aligned} \overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C} & =(\overrightarrow{O A}+\overrightarrow{A C})+\overrightarrow{O C} \\ & =\overrightarrow{O C}+\overrightarrow{O C}\end{aligned}$

$=2 \overrightarrow{O C}$

Hence, the answer is $\begin{aligned} & \qquad \\ & =2 \overrightarrow{O C}\end{aligned}$

Summary

Vector addition is a fundamental operation that enables the combination of vectors to determine resultant quantities in both geometric and algebraic contexts. Understanding vectors and their addition helps us to solve a variety of problems. Knowledge of vectors helps us to analyze and solve real-life problems.