Vector Triple Product

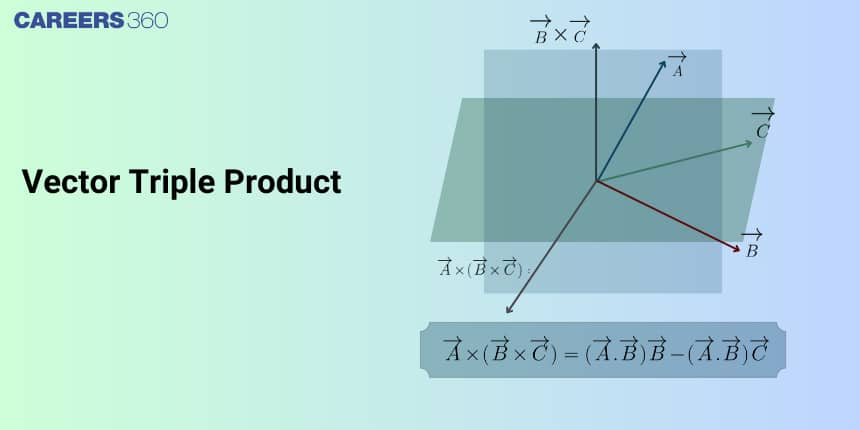
Vector Triple Product in Vector Algebra – Definition and Formula

The Vector Triple Product is an important concept in Vector Algebra that involves three vectors and a combination of cross and dot products. It is defined as the cross product of one vector with the cross product of the other two vectors. The result of a vector triple product is always a vector, not a scalar.

It is generally written as:
$\vec{a} \times (\vec{b} \times \vec{c})$

One special and useful property of the vector triple product is that its resultant vector always lies in the plane formed by the vectors $\vec{b}$ and $\vec{c}$. This makes it extremely helpful in simplifying complex vector expressions and solving geometrical and physical problems.

Definition of Vector Triple Product

The Vector Triple Product is defined as the vector obtained when one vector is crossed with the cross product of two other vectors.

For three vectors $\vec{a}$, $\vec{b}$, and $\vec{c}$, the vector triple product is:
$\vec{a} \times (\vec{b} \times \vec{c})$

It represents a vector combination that can be simplified using dot products, making calculations easier and more efficient.

Formula of Vector Triple Product

The formula of the vector triple product is given by the well-known identity:

$\vec{a} \times (\vec{b} \times \vec{c})
= (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b})\vec{c}$

This formula is extremely useful because it converts a complicated cross–cross product into a simple linear combination of vectors $\vec{b}$ and $\vec{c}$.

Important Properties of Vector Triple Product

We have provided below the important properties of the vector triple product:

Result Lies in the Plane of Two Vectors

The vector $\vec{a} \times (\vec{b} \times \vec{c})$ always lies in the plane containing $\vec{b}$ and $\vec{c}$.

Not Commutative

In general, $\vec{a} \times (\vec{b} \times \vec{c}) \ne (\vec{a} \times \vec{b}) \times \vec{c}$

Used to Simplify Vector Expressions

The vector triple product identity is widely used to simplify expressions in physics, engineering, and advanced vector geometry.

Derivation of Vector Triple Product

Proof of Vector Triple Product Formula

Let
$\vec{p}=\vec{a} \times(\vec{b} \times \vec{c})$

Since $\vec{p}$ is a cross product, it is perpendicular to both $\vec{a}$ and $(\vec{b} \times \vec{c})$.
But $\vec{b} \times \vec{c}$ itself is perpendicular to the plane formed by $\vec{b}$ and $\vec{c}$.
Hence, $\vec{p}$ must lie in the plane of $\vec{b}$ and $\vec{c}$.

Therefore, $\vec{p}$ can be expressed as a linear combination of $\vec{b}$ and $\vec{c}$:

$\vec{p}=l\vec{b}+m\vec{c}$ ...(i)

where $l$ and $m$ are scalars.

Finding the Values of Scalars

Taking dot product of equation (i) with $\vec{a}$:

$\vec{p}\cdot\vec{a}=l(\vec{a}\cdot\vec{b})+m(\vec{a}\cdot\vec{c})$

But
$\vec{p}=\vec{a}\times(\vec{b}\times\vec{c})$ is perpendicular to $\vec{a}$,
so

$\vec{p}\cdot\vec{a}=0$

Hence,

$l(\vec{a}\cdot\vec{b})+m(\vec{a}\cdot\vec{c})=0$

or

$l(\vec{a}\cdot\vec{b})=-m(\vec{a}\cdot\vec{c})$

Let

$\frac{l}{\vec{a}\cdot\vec{c}}=\frac{-m}{\vec{a}\cdot\vec{b}}=\lambda$

Then,

$l=\lambda(\vec{a}\cdot\vec{c})$
$m=-\lambda(\vec{a}\cdot\vec{b})$

Substituting in equation (i):

$\vec{a} \times(\vec{b} \times \vec{c})
=\lambda[(\vec{a}\cdot\vec{c})\vec{b}-(\vec{a}\cdot\vec{b})\vec{c}]$

Determination of $\lambda$

Choose simple vectors:
$\vec{a}=\hat{i},; \vec{b}=\hat{i},; \vec{c}=\hat{j}$

Then,

$\hat{i}\times(\hat{i}\times\hat{j})
=\lambda[(\hat{i}\cdot\hat{j})\hat{i}-(\hat{i}\cdot\hat{i})\hat{j}]$

$\hat{i}\times\hat{k}
=\lambda[0\cdot\hat{i}-1\cdot\hat{j}]$

$-\hat{j}=-\lambda\hat{j}$

So,

$\lambda=1$

Hence, the final identity becomes:

Vector Triple Product Formula

$\vec{a} \times(\vec{b} \times \vec{c})
=(\vec{a}\cdot\vec{c})\vec{b}-(\vec{a}\cdot\vec{b})\vec{c}$

This is the standard Vector Triple Product Identity.

Important Vector Triple Product Identities

$\vec{a} \times(\vec{b} \times \vec{c})
=(\vec{a}\cdot\vec{c})\vec{b}-(\vec{a}\cdot\vec{b})\vec{c}$

$(\vec{a} \times \vec{b}) \times \vec{c}
=(\vec{c}\cdot\vec{a})\vec{b}-(\vec{c}\cdot\vec{b})\vec{a}$

2. In general,

$\vec{a} \times(\vec{b} \times \vec{c})
\neq (\vec{a} \times \vec{b}) \times \vec{c}$

Equality holds only when $\vec{a}$ and $\vec{c}$ are collinear.

Properties of Vector Triple Product

Provided below are the properties of vector triple product:

Vector Quantity

The vector triple product is always a vector.

Not Associative

$\vec{a} \times(\vec{b} \times \vec{c})
\neq (\vec{a} \times \vec{b}) \times \vec{c}$

Perpendicular Nature

$\vec{a} \times(\vec{b} \times \vec{c})$ is perpendicular to both:

• $\vec{a}$

• $(\vec{b} \times \vec{c})$

Lies in the Plane

$\vec{a} \times(\vec{b} \times \vec{c})$ always lies in the plane of $\vec{b}$ and $\vec{c}$.

Solved Examples Based on Vector Triple Product

Example 1: If $\vec{a}, \vec{b}, \vec{c}$ are three non-zero vectors and $\hat{n}$ is a unit vector perpendicular to $\hat{c}$ such that $\vec{a}=\alpha \vec{b}-\hat{n}(a \neq 0)$ and $\vec{b} \cdot \vec{c}=12$, then $|\vec{c} \times(\vec{a} \times \vec{b})|_{\text {is equal to: }}$
[JEE MAINS 2023]
Solution

$
\begin{aligned}
& \overrightarrow{\mathrm{a}}=\alpha \overrightarrow{\mathrm{b}}-\hat{\mathrm{n}}, \vec{b} \cdot \overrightarrow{\mathrm{c}}=12 \\
& \overrightarrow{\mathrm{c}} \times(\vec{a} \times \vec{b})=(\vec{c} \cdot \vec{b}) \vec{a}-(\vec{c} \cdot \vec{a}) \vec{b} \\
& \overrightarrow{\mathrm{c}} \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})=12 \vec{a}-(\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{b}}) \\
& \because \overrightarrow{\mathrm{a}}=\alpha \overrightarrow{\mathrm{b}}-\mathrm{n}
\end{aligned}
$
$
\vec{c} \cdot \vec{a}=\alpha \overrightarrow{\mathrm{c}} \cdot \vec{b}-\vec{c} \cdot \mathrm{n}
$
$
\vec{c} \cdot \vec{a}=12 \alpha
$
$
\begin{aligned}
& \vec{c} \times(\vec{a} \times \vec{b})=12 \vec{a}-12 \alpha \vec{b} \\
& |\vec{c} \times(\vec{a} \times \vec{b})|=12|\vec{a}-\alpha \vec{b}| \quad[\because \vec{a}-\alpha \vec{b}=-n \text { then }|\vec{a}-\alpha \vec{b}|=1] \\
& \Rightarrow|\vec{c} \times(\vec{a} \times \vec{b})|=12
\end{aligned}
$
$
|\overrightarrow{\mathrm{c}} \times(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}})|=12
$
Hence, the answer is 12

Example 2: Let $\lambda \in \mathbb{R}, \vec{a}=\lambda \hat{\imath}+2 \hat{\jmath}-3 \hat{k}, \vec{b}=\hat{\imath}-\lambda \hat{\jmath}+2 \hat{k}{ }_{\operatorname{If}}((\vec{a}+\vec{b}) \times(\vec{a} \times \vec{b})) \times(\vec{a}-\vec{b})=8 \hat{\imath}-40 \hat{\jmath}-24 \hat{k}$, then $|\lambda(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|^2$ is equal to
Solution

$
\begin{aligned}
& ((\vec{a}+\vec{b}) \times(\vec{a} \times \vec{b}) \times(\vec{a}-\vec{b})-=8 \hat{i}-40 \hat{j}-24 \hat{k} \\
& \Rightarrow(\vec{a} \times(\vec{a} \times \vec{b})+\vec{b} \times(\vec{a} \times \vec{b})) \times(\vec{a}-\vec{b}) \\
& \Rightarrow((\vec{a} \cdot \vec{b}) \vec{a}-(\vec{a} \cdot \vec{a}) \vec{b}+(\vec{b} \cdot \vec{b}) \vec{a}-(\vec{b} \cdot \vec{a}) \vec{b}) \times(\vec{a}-\vec{b}) \\
& \Rightarrow 0-(\vec{a} \cdot \vec{b})(\vec{a} \times \vec{b})-a^2(\vec{b} \times \vec{a})+0-\mathrm{b}^2(\vec{a} \times \vec{b})-(\vec{a} \cdot \vec{b}) \vec{b} \times \vec{a}=8 \hat{\mathrm{i}}-40 \hat{\mathrm{j}}-24 \hat{\mathrm{k}} \\
& \Rightarrow\left(\mathrm{a}^2-\mathrm{b}^2\right)(\vec{a} \times \overrightarrow{\mathrm{b}})=8 \hat{\mathrm{i}}-40 \hat{\mathrm{j}}-24 \hat{\mathrm{k}} \\
& \left(\left(\lambda^2+4+9\right)-\left(1+\lambda^2+4\right)\right)(\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}) \\
& 8(\vec{a} \times \vec{b})=8(\hat{\mathrm{i}}-5 \hat{j}-3 \hat{k}) \\
& \hat{\mathrm{i}}(4-3 \lambda)-\hat{\mathrm{j}}(2 \lambda+3)+\hat{\mathrm{k}}\left(-\lambda^2-2\right)=\hat{\mathrm{i}}-5 \hat{\mathrm{j}}-3 \hat{\mathrm{k}} \\
& \Rightarrow 4-3 \lambda=1 \quad 2 \lambda+3=5 \quad-\lambda^2-2=-3 \\
& 3 \lambda=3 \\
& \lambda=1 \\
& \lambda \\
& \begin{array}{l}
\lambda^2=1
\end{array} \\
& \begin{array}{ll}
\lambda(\vec{a}+\vec{b}) \times(\vec{a}-\vec{b})|=|(\vec{a}+\vec{b}) \times\left.(\vec{a}-\vec{b})\right|^2 \\
\Rightarrow|-\vec{a} \times \vec{b}+\vec{b} \times \vec{a}|^2=|2(\vec{a} \times \vec{b})|^2=4(1+25+9)=140
\end{array}
\end{aligned}
$
Hence, the answer is 140

Example 3: Let $\vec{a}, \vec{b}$ and $\vec{c}$ be three non-zero vectors such that $\vec{b} \cdot \vec{c}=0$ and $\vec{a} \times(\vec{b} \times \vec{c})=\frac{b-\vec{c}}{2}$. If $\vec{d}$ be a vector such that $\vec{b} \cdot \vec{d}=\vec{a} \cdot \vec{b}$, then $(\vec{a} \times \vec{b}) \cdot(\vec{c} \times \vec{d})_{\text {is equal to }}$.
[JEE MAINS 2023]

Solution

We are given $\vec{b}\cdot\vec{c}=0$ and $\vec{a}\times(\vec{b}\times\vec{c})=\dfrac{\vec{b}-\vec{c}}{2}$

Use the vector triple product identity

$\vec{a}\times(\vec{b}\times\vec{c})=\vec{b}(\vec{a}\cdot\vec{c})-\vec{c}(\vec{a}\cdot\vec{b})$

So, $\vec{b}(\vec{a}\cdot\vec{c})-\vec{c}(\vec{a}\cdot\vec{b})=\dfrac{\vec{b}-\vec{c}}{2}$

Compare coefficients of $\vec{b}$ and $\vec{c}$ on both sides.

For $\vec{b}$: $\vec{a}\cdot\vec{c}=\dfrac{1}{2}$

For $\vec{c}$: $-(\vec{a}\cdot\vec{b})=-\dfrac{1}{2}$

So, $\vec{a}\cdot\vec{b}=\dfrac{1}{2}$

Now we are given $\vec{b}\cdot\vec{d}=\vec{a}\cdot\vec{b}=\dfrac{1}{2}$

We need to find $(\vec{a}\times\vec{b})\cdot(\vec{c}\times\vec{d})$

Use the identity

$(\vec{p}\times\vec{q})\cdot(\vec{r}\times\vec{s})=(\vec{p}\cdot\vec{r})(\vec{q}\cdot\vec{s})-(\vec{p}\cdot\vec{s})(\vec{q}\cdot\vec{r})$

So, $(\vec{a}\times\vec{b})\cdot(\vec{c}\times\vec{d})=(\vec{a}\cdot\vec{c})(\vec{b}\cdot\vec{d})-(\vec{a}\cdot\vec{d})(\vec{b}\cdot\vec{c})$

But $\vec{b}\cdot\vec{c}=0$, hence the second term vanishes.

So, $(\vec{a}\times\vec{b})\cdot(\vec{c}\times\vec{d})=(\vec{a}\cdot\vec{c})(\vec{b}\cdot\vec{d})$

Substitute known values:

$\vec{a}\cdot\vec{c}=\dfrac{1}{2}$

$\vec{b}\cdot\vec{d}=\dfrac{1}{2}$

Therefore, $(\vec{a}\times\vec{b})\cdot(\vec{c}\times\vec{d})=\dfrac{1}{2}\cdot\dfrac{1}{2}$

$=\dfrac{1}{4}$

Hence, the answer is $\frac{1}{4}$.

Example 4: Let $\vec{a}, \vec{b}, \vec{c}$ be three vectors mutually perpendicular to each other and have the same magnitude. If a vector $\vec{r}$ satisfies $\vec{a} \times\{(\vec{r}-b) \times \vec{a}\}+b \times\{(\vec{r}-\vec{c}) \times b\}+\vec{c} \times\{(\vec{r}-\vec{a}) \times \vec{c}\}=0$,then $\vec{r}$ is equal to:
Solution: $|\vec{a}|=|\vec{b}|=|\vec{c}|$ and $\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{c}=\vec{c} \cdot \vec{a}=0$
Let $\vec{r}=x \vec{a}+y \vec{b}+z \vec{c}$
where $\vec{r} \cdot \vec{a}=x|\vec{a}|^2, \vec{r} \cdot \vec{b}=y|\vec{b}|^2, \vec{r} \cdot \vec{c}=z|\vec{c}|^2$
Give expression is

$
\begin{aligned}
& (\vec{a} \times(\vec{r} \times \vec{a}))-(\vec{a} \times(\vec{b} \times \vec{a}))+\vec{b} \times(\vec{r} \times \vec{b})-\vec{b} \times(\vec{c} \times \vec{b})+ \\
& \vec{c} \times(\vec{r} \times \vec{c})-(\vec{c} \times(\vec{a} \times c))=0 \\
& \Rightarrow(\vec{a} \cdot \vec{r}) \vec{a}-|\vec{a}|^2 \vec{r}-(\vec{a} \cdot \vec{b}) \vec{a}+|\vec{a}|^2 \vec{b}+(\vec{b} \cdot \vec{r}) \vec{b}-|\vec{b}|^2 \vec{r}- \\
& (\vec{b} \cdot \vec{c}) \vec{b}+|\vec{b}|^2 \vec{c}+(\vec{c} \cdot \vec{r}) \vec{c}-|\vec{c}|^2 \vec{r}-(\vec{c} \cdot \vec{a}) \vec{a}+|\vec{c}|^2 \vec{a}=0 \\
& \Rightarrow x|\vec{a}|^2 \vec{a}+y|\vec{b}|^2 \vec{b}+z|\vec{c}|^2 \vec{c}-\vec{r}\left(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2\right)+ \\
& |\vec{a}|^2 \vec{b}+|\vec{b}|^2 \vec{c}+|\vec{c}|^2 \vec{a}=0 \\
& \Rightarrow|\vec{a}|^2(x \vec{a}+y \vec{b}+z \vec{c})-3|\vec{a}|^2 \vec{r}+|\vec{a}|^2(\vec{a}+\vec{b}+\vec{c})=0 \\
& \Rightarrow 3 \vec{r}-\vec{r}=\vec{a}+\vec{b}+\vec{c} \\
& \Rightarrow \vec{r}=\frac{1}{2}(\vec{a}+\vec{b}+\vec{c})
\end{aligned}
$
Hence, the answer is $\frac{1}{2}(\vec{a}+\vec{b}+\vec{c})$

Example 5: Let three vector $\vec{a}, \vec{b}$ and $\vec{c}$ be such that $\vec{c}$ is coplanar with $\vec{a}$ and $\vec{b}, \vec{a} \cdot \vec{b}=7$ and $\vec{b}$ is perpendicular to $\vec{c}$, where $\vec{a}=-\hat{i}+\hat{j}+\hat{k}$ and $\vec{b}=2 \hat{i}+\hat{k}$. Then the value of $2|\vec{a}+\vec{b}+\vec{c}|_{\text {is }}^2$ $\qquad$
[JEE MAINS 2021]
Solution

$
\begin{aligned}
\vec{c} & =\lambda(\vec{b} \times(\vec{a} \times \vec{b})) \\
& =\lambda((\vec{b} \cdot \vec{b}) \vec{b}-(\vec{b} \cdot \vec{a}) \vec{b}) \\
& =\lambda(5(-\hat{i}+\hat{j}+\hat{k})+2 \hat{i}+\hat{k}) \\
& =\lambda(-3 \hat{i}+5 \hat{j}+6 \hat{k}) \\
\vec{c} & \cdot \vec{a}=7 \Rightarrow 3 \lambda+5 \lambda+6 \lambda=7 \\
\Rightarrow & \lambda=\frac{1}{2} \\
\therefore & 2\left|\left(\frac{-3}{2}-1+2\right) \hat{i}+\left(\frac{5}{2}+1\right) \hat{j}+(3+1+1) \hat{k}\right|^2 \\
& =2\left(\frac{1}{4}+\frac{49}{4}+25\right)=25+50=75
\end{aligned}
$
Hence, the answer is 75

List of Topics Related to Vector Algebra

Provided below is the list of topics which are related to vector triple product in vector algebra, to boost your understanding and strengthen your concepts:

Types of Vectors

Vectors and Scalars

Addition of Vectors and Subtraction of Vectors

Multiplication Of Vectors by a Scalar Quantity

Components Of A Vector Along And Perpendicular To Another Vector

NCERT Resources

This section offers well-organized NCERT-based resources, including clear notes and step-by-step solutions, to help you study strictly according to the syllabus. It focuses on building strong conceptual clarity in Vector Algebra.

NCERT Maths Class 12th Notes for Chapter 10 - Vector Algebra

NCERT Maths Class 12th Solutions for Chapter 10 - Vector Algebra

NCERT Maths Class 12th Exemplar Solutions for Chapter 10 - Vector Algebra

Practice Questions based on Vector Triple Product

This section includes carefully selected practice questions based on the Vector Triple Product to help you apply formulas and identities with confidence. It is designed to strengthen your problem-solving skills and improve accuracy through regular practice.

Proof Of The Vector Triple Product- Practice Question MCQ

We have provided below the practice questions based on the topics related to Vector Triple Product: