Angular Momentum of Electron - De Broglie's Explanation, FAQs

Edited By Vishal kumar | Updated on Sep 24, 2024 04:35 PM IST

Introduction:
The rotating equivalent of linear momentum is angular momentum in physics. Because it is a preserved measure, the total angular momentum of a sealed system remains constant. It is a significant quantity in physics. Angular momentum of electron formula is mvr or nh/2. In this article we will study in detail about angular momentum of an electron, quantisation of angular momentum, property of an electron moving in a circular orbit and orbital angular momentum of an electron. Also, the quantised meaning in Tamil is அளவிடப்பட்டது.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

Angular Momentum of Electron - De Broglie's Explanation, FAQs

Electron spin:

The spinning electron was successful in describing not only fine structure and the strange Zeeman Effect, but also other atomic phenomena.

The Bohr Sommerfeld quantum theory of elliptic orbits with relativity correction was in fair numerical agreement with the observed fine structure of hydrogen spectral lines. It however, suffered from two main drawbacks or downsides:

Firstly, Summerfield's relativistic explanation could not be applied for the spectral lines of atoms other than hydrogen. Alkali atoms' spectral lines, for example, are doublets with two near fine-structure components. The (single) optical electron in alkali atoms moves in a Bohr-like orbit with a large radius and low velocity. Therefore, the relativity effect would be too small to account for the large (compared with hydrogen) Fine-structure splitting observed in alkali lines.
Secondly, the simple quantum theory failed to explain the anomalous Zeeman Effect, that is, the splitting of atomic spectral lines into four, six or more components when the light source was placed in an external magnetic field.

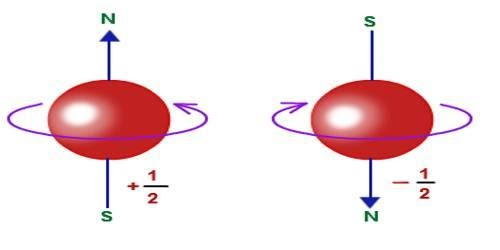
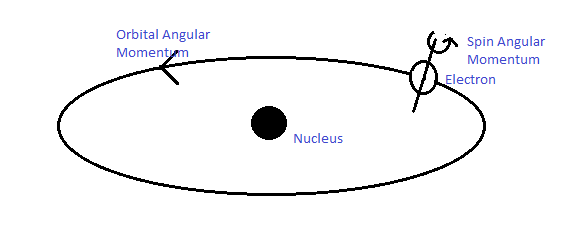
In an effort to remove these two drawbacks of the theory, Goudsmit and Uhlenbeck proposed in 1925 that an electron must be looked upon as a changed sphere spinning about its own axis, having an intrinsic (built-in) angular momentum and consequently an intrinsic magnetic dipole moment. These are called 'spin angular momentum' S and 'spin magnetic dipole moment' M, respectively.

Let us write the magnitude S of the spin angular momentum of the electron in terms of a 'spin quantum number’s, as we do for the orbital angular momentum L in terms of orbital quantum number l. Thus S

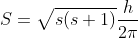
$S=\sqrt{s(s+1)}\frac{h}{2\pi}$
The only value which the spin quantum number can be given is s = ½, which confirms the observed fine-structures doubling.

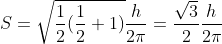
$S=\sqrt{\frac{1}{2}(\frac{1}{2}+1)}\frac{h}{2\pi}=\frac{\sqrt{3}}{2}\frac{h}{2\pi}$

The component of S along a magnetic field parallel to the z-direction is

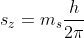
$s_z=m_s\frac{h}{2\pi}$

Where ms is the 'spin magnetic quantum number' and takes (2s + 1) = 2 values which are +s and -s, that is

m_s= +1/2 and-1/2

The gyromagnetic ratio for electron spin μ_s/S is double the equivalent ratio μ_L/L=e/2m, according to experimental evidence.

The spinning electron was successful in describing not only fine structure and the strange Zeeman Effect, but also other atomic phenomena. Although electron spin was proposed as a postulate, Dirac established in 1928 that an electron must have an intrinsic rotational momentum and an intrinsic magnetic moment using relativistic quantum mechanics.

Also read -

Experimental evidence of electron spin:

• AH Compton proposed that “the electron is probably the ultimate magnetic particle” in Compton Scattering (1921).

• Stern-Gerlach Experiment (1922): A beam of silver atoms was passed through an inhomogeneous magnetic field, and two beams of space quantized components were seen.

• Uhlenbeck and Goudsmit (1925) demonstrated that there are two angular momentum states: intrinsic angular momentum of the electron and "SPIN" angular momentum.

• Pauli Exclusion Principle (1925): no more than two electrons per orbital, or no two electrons with identical quantum numbers. A new quantum number has been proposed.

Postulate 6: Under all conditions, all electronic wave functions must be ant symmetric.

graphical representation of angular and orbital angular momentum.

Also read :

Theoretical Justification:

Dirac (1928) developed relativistic quantum theory & derived electron spin angular momentum

Orbital Angular Momentum

L = orbital angular momentum

Formula of orbital angular momentum/Orbital angular momentum formula,

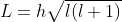
$L=h\sqrt{l(l+1)}$
l = orbital angular momentum quantum number

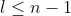
$l\leq n-1$
L_z = mℏ

m = 0, ±1, ±2… ±l

Spin Angular Momentum

S ≡ spin angular momentum

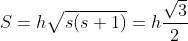
$S=h\sqrt{s(s+1)}=h\frac{\sqrt{3}}{2}$

s = spin angular momentum quantum number

s = ½

S = m_sℏ

m = ± 1/2

Related Topics Link,

Angular Momentum of Electron in Hydrogen Atom:

De Broglie's hypothesis can be used to compute the angular momentum of the hydrogen atom of an electron.

Consider an electron moving in a circular orbit of radius r.

According to the Broglie hypothesis, the associated wavelength of any particle is:

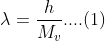
$\lambda =\frac{h}{M_v}....(1)$

From classical mechanics, the orbital angular momentum formula is:

L = Mvr …. (2) Also known as mvr formula

It is also noted that

2πr = mλ

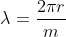
$\lambda =\frac{2\pi r}{m}$

By inserting the value of λ in equation (1), we get:

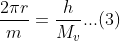
$\frac{2\pi r}{m}=\frac{h}{M_v}...(3)$

From equation 1 we can get:

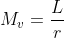
$M_v=\frac{L}{r}$

By substituting the Mv in equation (3) we get:

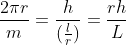
$\frac{2\pi r}{m}=\frac{h}{(\frac{l}{r})}=\frac{rh}{L}$

Now, solve this relation for angular momentum L:

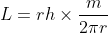
$L=rh\times \frac{m}{2\pi r}$

or, 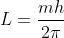$L=\frac{mh}{2\pi }$

or, 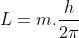$L=m.\frac{h}{2\pi}$

Here, 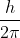$\frac{h}{2\pi}$ is designated as.

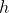So, the angular momentum of the electron of Hydrogen atom is:

L = m.ℏ

Here, m = 1, 2, 3, 4 …so on

Also, the angular momentum is quantized in units of ħ.

In hydrogen atom,

The radius of n^th orbit is

r_n∝n²/Z

NCERT Physics Notes :

Where, Z is atomic number

So,

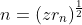$n=(zr_n)^\frac{1}{2}$ ....(1)

Angular momentum of an electron in an orbit is given by,

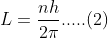
$L=\frac{nh}{2\pi}.....(2)$

Put value of n from (1) in equation (2)

Angular momentum of electron in nth orbit, 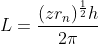$L=\frac{(zr_n)^{\frac{1}{2}}h}{2\pi}$

L ∝ r^1/2

L∝ √r

Hence, angular momentum of electron in hydrogen atom is proportional tor.

We can now tell the angular momentum in different orbits, say, angular momentum of electron in 5th orbit is 25h.

The following is a summary of everything we've learned so far about the energy and dispersion of an electron in a hydrogen atom:

The energy grows as n grows, and it is solely dependent on n, the fundamental quantum number.
As n grows, the average distance between the electron and the nucleus increases.
As n increases, the number of nodes in the probability distribution grows.
As l is increased, the electron density concentrates along certain lines (or in planes).

Bohr’s quantisation condition states: In Bohr’s model, the angular momentum of electrons orbiting around the nucleus is quantized on a condition that the electrons can move only in orbits with an integral multiple of h/2 angular momentum.

Also check-

Frequently Asked Questions (FAQs)

1. What is the angular momentum of an electron in 3rd orbit?

The angular momentum of electron in 3rd orbit is 9h.

2. What is the orbital angular momentum of a 3d electron?

The orbital angular momentum of 3d electron is6(h2π).

3. How can you say that angular momentum of an electron is quantised?

In Bohr’s model, the angular momentum of electrons orbiting around the nucleus is quantized on a condition that the electrons can move only in orbits with an integral multiple of h/2 angular momentum.

4. What is the formula for orbital angular momentum?

Orbital angular momentum formula, L = ℏl(l+1).

5. What is the formula for spin angular momentum?

Spin angular momentum formula, S = ℏs(s+1).

6. What is the orbital angular momentum of p electron?

h/2