Bar Magnet As An Equivalent Solenoid

In the realm of electromagnetism, the bar magnet stands out as a fundamental object of study due to its inherent magnetic properties. Remarkably, a bar magnet can be modelled as an equivalent solenoid, offering a simpler way to understand its magnetic field and behaviour. This equivalence arises because both bar magnets and solenoids produce a magnetic field through the alignment of magnetic domains or electric currents, respectively. In practical terms, this concept finds real-world applications in devices like electric motors and transformers, where solenoids generate magnetic fields in a controlled manner. In this article, we will understand the bar magnet as an equivalent solenoid and our comprehension of the magnetic field.

This Story also Contains

1. Pole Strength
2. Magnetic Dipole Moment
3. Solenoid
4. Bar Magnet as an Equivalent Solenoid
5. Solved Examples Based on Bar Magnet as an Equivalent Solenoid
6. Summary

Bar Magnet

A bar magnet, with its two poles—north and south—demonstrates fundamental magnetic properties that are pivotal in understanding magnetism. Interestingly, this seemingly simple object can be effectively modelled as an equivalent solenoid, a coil of wire through which current flows, creating a magnetic field. Both a bar magnet and a solenoid generate a magnetic field through the alignment of magnetic domains in the magnet or the electric current in the solenoid. A bar magnet consists of two equal and opposite magnetic poles separated by a small distance.

Pole Strength

Pole strength is a fundamental property of a bar magnet that quantifies the strength of its magnetic poles. It is defined as the measure of the intensity of the magnetic field produced by each pole of the magnet. In essence, pole strength determines how effectively a magnet can exert force on magnetic materials and influence magnetic fields. The strength of a magnetic pole to attract magnetic materials towards itself is known as pole strength.

It is a scalar quantity and it is represented by +m and -m. It depends on the nature of the material of the magnet and the area of the cross-section i.e. independent from the length.

Magnetic Dipole Moment

The magnetic dipole moment is a key concept in magnetism, representing the strength and orientation of a magnetic source. It is a vector quantity that describes the overall magnetic effect produced by a magnetic dipole, such as a bar magnet or a current loop. It represents the strength of the magnet. Mathematically it is defined as the product of the strength of either pole and effective length.

i.e for the below figure $\vec{M}=m L=m(2 l)$

It is a vector quantity directed from south to north.

This is analogous to the electrical dipole moment which was given by $\vec{P}=q L$

And using this analogy we can calculate

The magnetic Field on the Axial Position of a Bar Magnet

For $r \gg a \quad \Rightarrow B_{\text {axial }}=\frac{\mu_o 2 M}{4 \pi r^3}$

Magnetic Field at the Equatorial Position of a Magnet

The magnetic field at the equatorial position of a bar magnet refers to the region located midway between the north and south poles of the magnet. At this position, the magnetic field is oriented perpendicular to the axis of the magnet and is characterized by its unique properties. Unlike the field lines near the poles, which are dense and strong, the field at the equatorial position is weaker and more spread out.

$
B_e=\frac{\mu_o}{4 \pi} \frac{M}{\left(r^2+a^2\right)^{\frac{3}{2}}}
$

And for
For $r \gg a \quad \Rightarrow B_e=\frac{\mu_o M}{4 \pi r^3}$

Magnetic Field at any general point due to bar magnet

$B_g=\frac{\mu_o}{4 \mu} \frac{M}{r^3} \sqrt{3 \cos ^2 \theta+1}$

Solenoid

A solenoid is a fundamental component in electromagnetism, consisting of a coil of wire wound in a helical shape. When an electric current passes through the wire, it generates a magnetic field along the axis of the solenoid, creating a uniform magnetic field within its core. The solenoid is defined as a cylindrical coil of many tightly wound turns of insulated wire with a general diameter of the coil smaller than its length.

Bar Magnet as an Equivalent Solenoid

By calculating the axial field of a finite solenoid carrying current and equating it with the magnetic field of a bar magnet we can demonstrate a Bar magnet as an equivalent solenoid.

For the above figure

Let n = number of turns per unit length $\frac{N}{L}$

where, N = total number of turns,

$L=2 l=$ length of the solenoid

We will take an elemental circular current-carrying loop of thickness dx and radius R at a distance x from the centre of the solenoid.

So the number of turns per unit length for the elemental loop will be $n=\frac{N}{d x}$

The magnetic field at point P due to an elemental loop is given as $d B=\frac{\mu_0(n d x) I R^2}{2\left\{(r-x)^2+R^2\right\}^{3 / 2}}$

for $r \gg R$ and $r \gg x$
$
d B=\frac{\mu_0(n d x) I R^2}{2 r^3}
$

Integrating x from $-l$ to $+l$ we get the magnitude of the total field as

$
B=\int_{-l}^l \frac{\mu_0 n I R^2}{2 r^3} d x=\frac{\mu_0 n I R^2}{2 r^3} \int_{-l}^l d x=\frac{\mu_0 n I R^2}{2 r^3} *(2 l)
$

Now divide and multiply by $\pi$
$
\Rightarrow \vec{B}=\frac{\mu_0(n 2 l) I \pi R^2}{2 \pi r^3}
$

Using $N=n(2 l)$

we get $\vec{B}=\frac{\mu_0 N I \pi R^2}{2 \pi r^3}$

Now if we consider the above solenoid as a Bar magnet then its dipole moment is given by $\vec{M}=N I A$

Now using $A=\pi R^2$ we can write $\vec{B}=\frac{\mu_0 N I A}{2 \pi r^3}=\frac{\mu_0 \vec{M}}{2 \pi r^3}=\frac{2 \mu_0 \vec{M}}{4 \pi r^3}$

$\vec{B}=\frac{2 \mu_0 \vec{M}}{4 \pi r^3}$ This is equivalent to the magnetic field on the Axial Position of a bar magnet.

Solved Examples Based on Bar Magnet as an Equivalent Solenoid

Example 1: Magnetic intensity for an axial point due to a short bar magnet of magnetic moment M is given by

1) $\frac{\mu_o}{4 \pi} \times \frac{M}{d^3}$
2) $\frac{\mu_o}{4 \pi} \times \frac{M}{d^2}$
3) $\frac{\mu_o}{2 \pi} \times \frac{M}{d^3}$
4) $\frac{\mu_o}{2 \pi} \times \frac{M}{d^2}$

Solution:

Magnetic field on Axial Position of bar magnet

$B_{\text {axial }}=\frac{\mu_o 2 M}{4 \pi r^3}$

wherein

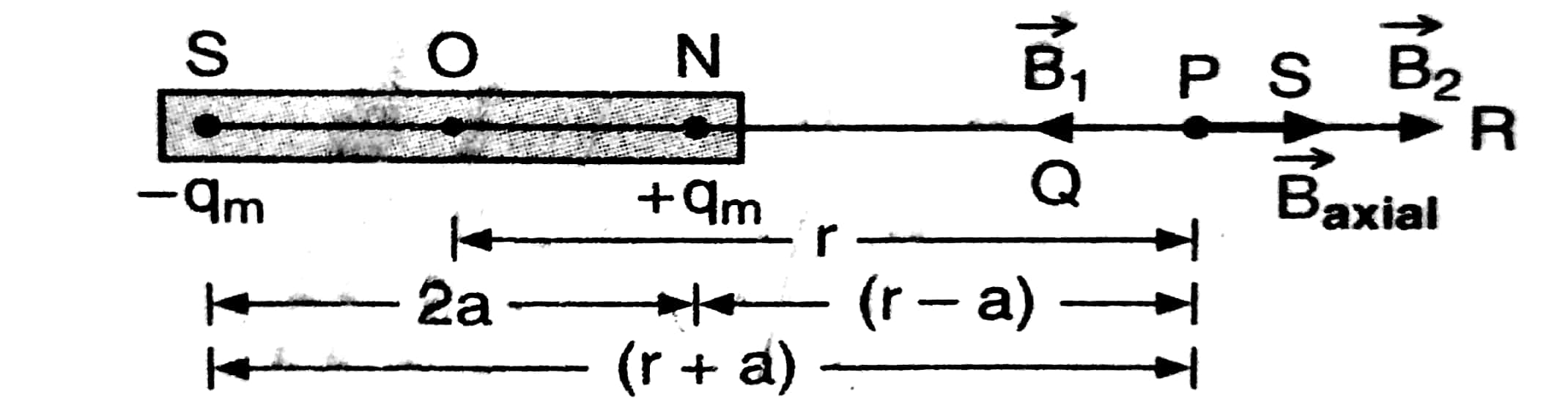
$B_a=\frac{\mu_o}{4 \pi} \times \frac{2 M}{d^3}=\frac{\mu_o}{2 \pi} \times \frac{M}{d^3}$

Hence, the answer is the option (3).

Example 2: Two magnetic dipoles X and Y are placed at a separation d, with their axes perpendicular to each other. The dipole moment of Y is twice that of X. A particle of charge q is passing through their midpoint P at angle $\theta=45^{\circ}$ with the horizontal line, as shown in the figure. what would be the magnitude of the force on the particle at that instant? (d is much larger than the dimensions of the dipole)

$
\text { 1) }\left(\frac{\mu_0}{4 \pi}\right) \frac{M}{\left(\frac{d}{2}\right)^3} \times q v
$
2) 0

3) $\sqrt{2}\left(\frac{\mu_0}{4 \pi}\right) \frac{M}{\left(\frac{d}{2}\right)^3} \times q v$

4) $\left(\frac{\mu_0}{4 \pi}\right) \frac{2 M}{\left(\frac{d}{2}\right)^3} \times q v$

Solution:

For short or ideal dipole

The magnetic field on the axial position of a bar magnet

$\vec{B}_{\text {axial }}=\frac{\mu_o 2 \vec{M}}{4 \pi r^3}$

The magnetic field on the equatorial position of a bar magnet

$\vec{B}_{\text {equatorial }}=\frac{\mu_o(-\vec{M})}{4 \pi r^3}$

$\begin{aligned} & B_1=\left(\frac{\mu_0}{4 \pi}\right) \frac{2 M}{\left(\frac{d}{2}\right)^3} \\ & B_2=\left(\frac{\mu_0}{4 \pi}\right) \frac{2 M}{\left(\frac{d}{2}\right)^3} \\ & B_1=B_2\end{aligned}$

The net magnetic field will be at $45^{\circ}$

The direction of B_net & velocity of charge is the same,

Hence, the charge will experience no force.

Hence, the answer is the option (2).

Example 3: A bar magnet is placed north-south with its pole due north. The points of zero magnetic field will be in which direction from the centre of the magnet:

1) North and South

2) East and west

3) Northeast and Southwest

4) Northwest and southeast

Solution:

Bar Magnet in Magnetic Field

When a bar magnet is left free in a uniform magnetic field, it aligns itself in the directional field.

Property of Bar magnet

Hence, the answer is the option (1).

Example 4: An insulating thin rod of length l has a linear charge density $\rho(x)=\rho_0 \frac{x}{l}$ on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time-averaged magnetic moment of the rod is

1) $\pi n \rho_0 l^3$
2) $\frac{\pi}{3} n \rho_0 l^3$
3) $\frac{\pi}{4} n \rho_0 l^3$
4) $n \rho_0 l^3$

Solution:

Magnetic moment (M)

M=NiA

wherein

N- number of turns in the coil

i- current throughout the coil

A- area of the coil

Assuming a dx element at a distance x from point O.

$\begin{aligned} & \text { Then } d q=\lambda d x \\ & \begin{array}{l}A=\pi x^2 \\ M=N I A \\ d m=\int_0^l\left(\rho_0 \frac{x}{l}\right) \cdot n \cdot d x \cdot \pi x^2 \\ M=\frac{n \rho_o \pi}{l} \int_o^l x^3=\frac{n \rho_o \pi}{l} \frac{l^4}{4} \\ M=\frac{\pi}{4} n \rho_o l^3\end{array}\end{aligned}$

Hence, the answer is the option (3).

Example 5: In a vibrational magnetometer the time period of a suspended bar magnet can be reduced by

1) Moving it towards the south

2) Moving it towards the North

3) Moving it towards the Equator

4) None of these

Solution:

SHM of Bar Magnet in a Magnetic Field

$T=2 \pi \sqrt{\frac{I}{M B}}$

$\begin{aligned} & I \rightarrow \text { Moment of Inertia of magnet } \\ & M \rightarrow \text { The magnetic moment of the magnet } \\ & B \rightarrow \text { Magnetic field }\end{aligned}$

wherein

In a uniform Magnetic field Bar magnets perform SHM.

Formula

At the equator, B_H increases

$T=2 \pi \sqrt{\frac{I}{m B}} \Rightarrow B_H \uparrow \& T \downarrow$

Hence, the answer is the option (1).

For more information, the below video can be referred to:

Summary

The bar magnet, with its distinct north and south poles, can be modelled as an equivalent solenoid, providing a simplified view of its magnetic field. The pole strength, magnetic dipole moment, and field calculations at various positions (axial and equatorial) highlight the magnet's behaviour. By equating a solenoid's field to that of a bar magnet, we can understand and apply these principles in real-world applications such as electric motors and transformers. Examples demonstrate how these concepts are used to solve practical problems in electromagnetism.