Bending A Cyclist

Bending while cycling is more than just a posture; it's a blend of physics and precision that directly impacts a cyclist's performance. Whether you're cruising down a city street or racing on a competitive track, the way a cyclist bends their body plays a crucial role in aerodynamics, balance, and speed. This bending action isn't just about looking streamlined; it minimizes air resistance, allowing the cyclist to conserve energy and maintain higher speeds. In real life, this concept parallels how we often adjust our approach to overcome obstacles—just as a cyclist bends to cut through the wind, we too must adapt and streamline our efforts to navigate life's challenges efficiently.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Bending a Cyclist
2. Solved Examples Based on Bending a Cyclist
3. Summary

Bending a Cyclist

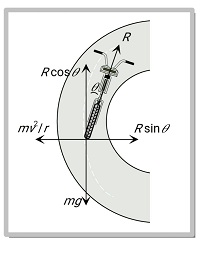
Bending a cyclist refers to the technique a cyclist uses to navigate turns at high speeds by leaning or "bending" into the curve. This action is crucial for maintaining balance and stability while turning, as it counteracts the centrifugal force that pushes the cyclist outward. The lean creates an inward force that keeps the cyclist on their desired path, preventing them from skidding or tipping over. In real life, this principle is observed in competitive cycling, motorcycling, and even when a person rides a bicycle around a corner.

From figure.

$
\begin{aligned}
& R \sin \theta=\frac{m v^2}{r} .....(i) \\
& R \cos \theta=m g ...... (ii)
\end{aligned}
$
(i) \& (ii)
$
\begin{aligned}
& \tan \theta=\frac{v^2}{r g} \\
& \theta=\tan ^{-1}\left(\frac{v^2}{r g}\right)
\end{aligned}
$

$V=$ velocity
$\mathrm{r}=$ radius of track
$\theta=$ angle with which the cycle leans.

Recommended Topic Video

Solved Examples Based on Bending a Cyclist

Example 1: A cyclist goes on a round circular path with a constant speed of 30m/s. If the radius of the path is 90m then the angle made by him with vertical will be:

1) $30^{\circ}$
2) $45^0$
3) $20^{\circ}$
4) $10^{\circ}$

Solution:

Bending a Cyclist

From figure.
$$
R \sin \theta=\frac{m v^2}{r}
$$
$$
R \cos \theta=m g
$$

(i) $\&$ (ii)

$$
\begin{aligned}
& \tan \theta=\frac{v^2}{r g} \\
& \theta=\tan ^{-1}\left(\frac{v^2}{r g}\right)
\end{aligned}
$$

$V=$ velocity
$r=$ radius of track
$\theta=$ angle with which the cycle leans

So,

$$
R \sin \theta=\frac{m v^2}{r}
$$
$$
R \cos \theta=m g
$$

by (i) and (ii)

$$
\begin{aligned}
& \tan \theta=\frac{v^2}{r g} \Rightarrow \theta=\tan ^{-1}\left(\frac{v^2}{r g}\right)=\tan ^{-1}\left(\frac{30 \times 30}{10 \times 90}\right)=\tan ^{-1}(1) \\
& \theta=45^{\circ}
\end{aligned}
$$

Hence, the answer is the option (2).

Example 2: A cyclist is moving with a velocity of 20m/s. if he wants to take a particular turn of radius of 40 m then for his safe turn what should be the value of the angle made by the cyclist with vertical $\left(g=10 \mathrm{~m} / \mathrm{s}^2\right)$

1) $60^{\circ}$
2) $75^{\circ}$
3) $45^{\circ}$
4) $30^{\circ}$

Solution

Bending a Cyclist

From figure.
$$
\begin{aligned}
& R \sin \theta=\frac{m v^2}{r} \\
& R \cos \theta=m g
\end{aligned}
$$

from eq. (i) \& (ii)

$$
\begin{aligned}
& \tan \theta=\frac{v^2}{r g} \\
& \theta=\tan ^{-1}\left(\frac{v^2}{r g}\right)
\end{aligned}
$$

$\mathrm{V}=$ velocity
$r=$ radius of track
$\theta=$ angle with which the cycle leans

wherein

The radius of the curve is small.

The velocity of the cyclist is large.

From diagram
$$
\begin{aligned}
& R \sin \theta=\frac{m v^2}{r} \ldots . .(1) \\
& R \cos \theta=m g \ldots .(2) \\
& \tan \theta=\frac{v^2}{r g}=\frac{20 \times 20}{40 \times 10}=1 \\
& \theta=45^{\circ}
\end{aligned}
$$

Hence, the answer is the option (3).

Summary

Whenever a cyclist leans into a turn, what is actually happening is that they are balancing the force located at their centre of gravity out versus the centripetal and gravity forces attributed to that balance. As they negotiate a curve, the centripetal force pulls the motorist toward the centre of curvature, which inertia resists. Any such occurrence means that the cyclist is putting much effort to counterline the acting forces. In so doing, the biker develops a case of momentums balancing each other force of gravity pulling him down and the centripetal force inwards. This very most unfortunate or can be accomplished by leaning to one side such that the balance between gravitational to centripetal force will be achieved, and no turn will ever make the biker fall or skid. This understanding of the balance of the actions of the two forces of these balances allows a cyclist to make safe and efficient turns, which is a basic skill in both recreational and competitive cycling.