Calculation Of Necessary Force In Different Conditions On Rough Surface

Force is a basic concept in physics that describes any interaction that, when unopposed, will change the motion of an object. This encompasses things like causing objects to accelerate, decelerate, stay put, or alter course. In other words, force is a push or pull exerted on an object as a result of an interaction with another object.

This Story also Contains

1. Calculation of Necessary Force In Different Conditions On Rough Surface
2. Solved Examples Based on Calculation of Necessary Force in Different Conditions on Rough Surface
3. Summary

Newton's second law describes force quantitatively by equating it to the mass multiplied by the acceleration of an object undergoing the force (F = ma). The third of his laws of motion concludes that for the action to happen, an equivalent or opposite reaction will happen.

In this article, we will cover the concept of calculation of necessary force In different conditions on rough surfaces. This topic falls under the broader category of laws of motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of one question has been asked on this concept.

Let's read this entire article to gain an in-depth understanding of the Motion of blocks when connected with string.

Calculation of Necessary Force In Different Conditions On Rough Surface

Here we have six cases in which we will discuss forces in different conditions.

Case 1:- Minimum pulling force P at an angle α from the horizontal

By resolving P in the horizontal and vertical direction, we get

where F is the friction force.

For the condition of equilibrium,

$\begin{array}{rl}& F=P\cos \alpha \\ & R=W-P\sin \alpha \end{array}$

By substituting these values in F= μR, we get:

$\begin{array}{rl}& P\cos \alpha =\mu (W-P\sin \alpha )\\ & Use=\mu =\tan \theta \\ & \Rightarrow P\cos \alpha =\frac{\sin \theta }{\cos \theta }(W-P\sin \alpha )\\ & P=\frac{W\sin \theta }{\cos (\alpha -\theta )}\end{array}$

Where P is the pulling force, R is a normal reaction and W is the weight.

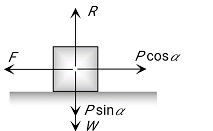
Case 2:- Minimum Pushing Force P at an Angle α From the Horizontal

By resolving P in the horizontal and vertical direction, we get:

For the condition of equilibrium,

$\begin{array}{rl}& F=P\cos \alpha \\ & R=W+P\sin \alpha \end{array}$

By substituting these values in F=μR, we get:

$\begin{array}{rl}& P\cos \alpha =\mu (W+P\sin \alpha )\\ & Use=\mu =\tan \theta \\ & \Rightarrow P\cos \alpha =\frac{\sin \theta }{\cos \theta }(W+P\sin \alpha )\\ & P=\frac{W\sin \theta }{\cos (\alpha +\theta )}\end{array}$

Case 3:- Minimum Pulling Force P to Move the Body Upwards on an Inclined Plane

By resolving P in the direction of the plane and perpendicular to the plane, we get:

For the condition of equilibrium

$\begin{array}{rl}& R+P\sin \alpha =W\cos \lambda \Rightarrow R=W\cos \lambda -P\sin \alpha \\ & F+W\sin \lambda =P\cos \alpha \Rightarrow F=P\cos \alpha -W\sin \lambda \end{array}$

By substituting these values in F=μR, we get:

$P=\frac{W\sin (\theta +\lambda )}{\cos (\alpha -\theta )}$

Where $\theta$ is the angle of friction such that, $\mu =\tan \theta$

Case 4: Minimum Force to Move a Body in a Downward Direction Along the Surface of the Inclined Plane

By resolving P in the direction of the plane and perpendicular to the plane, we get:

For the condition of equilibrium,

$\begin{array}{rl}& R+P\sin \alpha =W\cos \lambda \Rightarrow R=W\cos \lambda -P\sin \alpha \\ & F=P\cos \alpha +W\sin \lambda \end{array}$

By substituting these values in F=μR, we get:

$P=\frac{W\sin (\theta -\lambda )}{\cos (\alpha -\theta )}$

$\text{Where}\theta \text{is the angle of friction such that,}\mu =\tan \theta$

Case 5:- Minimum Force to Avoid Sliding of a Body Down on an Inclined Plane

As the block has tendency to slip downward, friction force will act up the incline. For the minimum value of P, the friction force is limiting and the block is in equilibrium.

Free Body Diagram of the block-

For the condition of equilibrium-

$\begin{array}{rl}& \mathrm{R}+\mathrm{P}\sin \alpha =\mathrm{mg}\cos \lambda \\ & \Rightarrow \mathrm{R}=\mathrm{mg}\cos \lambda -\mathrm{P}\sin \alpha \\ & \text{Limiting friction}-\\ & {\mathrm{f}}_l=\mu \mathrm{R}\\ & \Rightarrow f_l=\mu (mg\cos \lambda -P\sin \alpha )\dots \dots (1)\\ & f_l=mg\sin \lambda -P\cos \alpha \dots \text{(2)}\end{array}$

From equation (1) and (2)-

$\begin{array}{rl}& mg\sin \lambda -P\cos \alpha =\mu (mg\cos \lambda -P\sin \alpha )\\ & \theta \to \text{angle of friction}\\ & \mu =\tan \theta \\ & \mathrm{P}(\cos \alpha -\tan \theta \sin \alpha )=\mathrm{mg}(\sin \lambda -\tan \theta \cos \lambda )\\ & \Rightarrow P=\frac{mg\sin (\theta -\lambda )}{\cos (\theta +\alpha )}\end{array}$

Case 6:- Minimum Force of Motion Along the Horizontal Surface and its Direction

Let the force P be applied at an angle α with the horizontal.

Let the friction force on the block be F.

F.B.D of the block-

For vertical equilibrium,

$\begin{array}{rl}& \mathrm{R}+\mathrm{P}\sin \alpha =\mathrm{mg}\\ & \Rightarrow \therefore \mathrm{R}=\mathrm{mg}-\mathrm{P}\sin \alpha \end{array}$

And for horizontal motion,

$\mathrm{P}\cos \alpha \ge \mathrm{F}\Rightarrow \mathrm{P}\cos \alpha \ge \mu \mathrm{R}$

Substituting the value of R, we get:-

$\begin{array}{rl}\mathrm{P}\cos \alpha & \ge \mu (\mathrm{mg}-\mathrm{P}\sin \alpha )\\ \Rightarrow \mathrm{P}& \ge \frac{\mu \mathrm{mg}}{\cos \alpha +\mu \sin \alpha }\end{array}$

For the force P to be minimum $(\cos \alpha +\mu \sin \alpha )$ must be maximum i.e.,

$\begin{array}{rl}& \frac{\mathrm{d}}{\mathrm{d}\alpha }[\cos \alpha +\mu \sin \alpha ]=0\\ & \Rightarrow -\sin \alpha +\mu \cos \alpha =0\\ & \therefore \tan \alpha =\mu \\ & \Rightarrow \alpha ={\tan }^{-1}(\mu )=\text{angle of friction.}\end{array}$

i.e. For the minimum value of P, its angle from the horizontal should be equal to the angle of friction.

$\text{As}\tan \alpha =\mu \text{, so from the figure,}$

$\sin \alpha =\frac{\mu }{\sqrt{1+{\mu }^2}}\mathrm{and}\text{cos}\alpha =\frac{1}{\sqrt{1+{\mu }^2}}$

By substituting these values,
$\begin{array}{c}\mathrm{P}\ge \frac{\mu \mathrm{mg}}{\frac{1}{\sqrt{1+{\mu }^2}}+\frac{{\mu }^2}{\sqrt{1+{\mu }^2}}}\\ \Rightarrow \mathrm{P}\ge \frac{\mu \mathrm{mg}}{\sqrt{1+{\mu }^2}}\\ \therefore {\mathrm{P}}_{min}=\frac{\mu \mathrm{mg}}{\sqrt{1+{\mu }^2}}\end{array}$

Recommended Topic Video

Solved Examples Based on Calculation of Necessary Force in Different Conditions on Rough Surface

Example 1: A heavy box of mass 20 kg is pulled on a horizontal surface by applying a horizontal force. If the coefficient of kinetic friction between the box and the horizontal surface is 0.25, find the force of friction exerted (in N) by the horizontal surface on the box.

1) 39

2) 55

3) 45

4) 49

Solution:

In the verticle direction there is no acceleration, so, R = mg as the box slides on the horizontal surface, the surface exerts kinetic friction on the box. The magnitude of the kinetic friction is,

$f_k={\mu }_{k}R={\mu }_{k}mg=0.25\times 20\mathrm{kg}\times 9.8\mathrm{m}/{\mathrm{s}}^2=49\mathrm{N}$

Hence, the answer is option (4).

Example 2: A 100kg load is uniformly moved over a horizontal plane by a force F applied at an angle of ${30}^{\circ }$ to the horizontal. Find this force if the coefficient of friction between the load and the plane is 0.3. (g=10m/s²)

1) 250N

2) 300N

3) 295.26N

4) 200N

Solution:

Given

mass of the block, m=1000kg

$\text{Coefficient of friction,}\mu =0.2$

The velocity of the block is constant (uniform motion).

F.B.D of the block-

As the block is moving with constant velocity (no acceleration) the net force acting on the block must be zero.

$\begin{array}{rl}& \Rightarrow \mathrm{N}+\mathrm{F}\sin {30}^{\circ }\\ & \mathrm{N}=\mathrm{mg}-\frac{\mathrm{F}}{2}\\ & f=F\cos {30}^{\circ }=\frac{F\sqrt{3}}{2}\dots \end{array}$

Kinetic friction
$\begin{array}{rl}& f=\mu N\\ & \Rightarrow f=\mu (mg-\frac{F}{2}).\end{array}$

Comparing equation 1 and 2 -
$\begin{array}{rl}& \frac{F\sqrt{3}}{2}=\mu (mg-\frac{F}{2})\\ & \Rightarrow F=\frac{2\mu mg}{\sqrt{3}+\mu }=\frac{2000\times 0.3}{1.73+0.3}\\ & \Rightarrow F=295.26\end{array}$

Hence, the answer is option (3).

Example 3: What is the minimum pushing force (in N) just to move the block?

1) 50

2) 40

3) 55

4) 60

Solution:

Minimum Pushing Force P and Angle(alpha) From Horizontal

$\begin{array}{rl}& F=P\cos \alpha \\ & R=W+P\sin \alpha \\ & P\cos \alpha =\mu (W+P\sin \alpha )\\ & P=\frac{W\sin \theta }{\cos (\alpha +\theta )}\\ & \mu =\text{Coefficient of friction}\\ & \mathrm{w}=\text{weight}\\ & \mathrm{P}=\mathrm{P}\text{ulling force}\\ & \text{wherein}\\ & \text{Use}\\ & F=\mu R\\ & \mathrm{F}=\text{Force}\\ & \mathrm{R}=\text{Reaction}\end{array}$

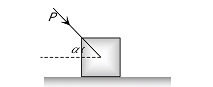
for just the tendency to move $P\cos {53}^{\circ }=f_l=P\cos {53}^{\circ }=\mu R$
$\begin{array}{rl}& P\ast \frac{3}{5}=0.60(5\ast 10-P\ast \frac{4}{5})\\ & P=0.6\ast 5\ast 10\ast \frac{3}{5}=50\mathrm{N}\end{array}$

Hence, the answer is option (1).

Example 4: A block of mass $\sqrt{3}\mathrm{kg}$ is kept on a rough surface having a coefficient of static friction $-2\sqrt{3}$. What is the minimum value of $F$ (in $N$ ) such that the block shown in the arrangement just starts moving?

1) 20

2) 10

3) 12

4) 15

Solution:

Given,

mass of the block, $m=\sqrt{3}\mathrm{kg}$ Coefficient of static friction, $\mu =\frac{1}{2\sqrt{3}}$

F.B.D of the block-

$N=mg+F\sin {60}^{\circ }$
limiting friction-
$\begin{array}{rl}& f=\mu N\\ & \Rightarrow f=\mu (mg+\frac{\sqrt{3}F}{2})\dots (1)\end{array}$

For the minimum value of F, the block will just begin to move unaccelerated.

f=F \cos 60^{\circ} \ldots (2)

Comparing equation (1) and equation (2)-

$\begin{array}{rl}& \frac{F}{2}=\mu (mg+\frac{\sqrt{3}F}{2})\\ & \Rightarrow F=\frac{2\mu mg}{1-\sqrt{3}\mu }\end{array}$

Substituting the values-

F=20 N

Hence, the answer is option (1).

Example 5: A heavy box is to be dragged along a rough horizontal floor. To do so, person $A$ pushes it at an angle ${30}^{\circ }$ from the horizontal and requires a minimum force $F_A$, while person $B$ pulls the box at an angle ${60}^{\circ }$ from the horizontal and needs minimum force ${\mathrm{F}}_{\mathrm{B}}$.If the coefficient of friction between the box and the floor is $\frac{\sqrt{3}}{5}$ the ratio $\frac{F_A}{F_B}$ is:

1) $\sqrt{3}$
2) $\frac{5}{\sqrt{3}}$
3) $\sqrt{\frac{3}{2}}$
4) $\frac{2}{\sqrt{3}}$

Solution:

In the First case, where the person pushes the box,

$\begin{array}{rl}& \mathrm{N}={\mathrm{F}}_{\mathrm{A}}\sin 30+\mathrm{mg}\\ & F_A\cos 30=f_r\\ & F_A\cos 30=\mu \mathrm{N}\\ & F_A\cos 30=\mu (mg+F_A\sin 30)\\ & F_A(\cos 30-\mu \sin 30)=\mu \mathrm{mg}\\ & F_A=\frac{\mu mg}{(\cos 30-\mu \sin 30)}\end{array}$

In the second case where the person pulls the box,

$\begin{array}{rl}& \mathrm{N}=\mathrm{mg}-{\mathrm{F}}_{\mathrm{B}}\sin 60\\ & F_B\cos 60=f_r\\ & F_B\cos 60=\mu N\\ & F_B\cos 60=\mu (mg-F_B\sin 60)\\ & F_B(\cos 60+\mu \sin 60)=\mu \mathrm{mg}\\ & {\mathrm{F}}_{\mathrm{B}}=\frac{\mu \mathrm{mg}}{(\cos 60+\mu \sin 60)}\end{array}$

From the above equation, we can say that

$\frac{F_A}{F_B}=\frac{(\cos 60+\mu \sin 60)}{(\cos 30-\mu \sin 30)}$

On solving we will get,
$\frac{{\mathrm{F}}_{\mathrm{A}}}{{\mathrm{F}}_{\mathrm{B}}}=\frac{2}{\sqrt{3}}$

Hence, the answer is option (4).

Summary

Force is one of the most central ideas in physics to drive the way objects influence one another and the changes in their motion. More precisely, it is defined as the interaction that can cause objects to accelerate, decelerate, change direction, or remain in place. Overall, force is the key concept underlying the physics of the physical world. Specifically, it is a vector quantity, meaning it has both magnitude and direction, which is important because it is critical for the accurate description of different interaction effects.

A study of the idea helps to base Newton's laws of motion, giving a framework within which to analyze how the forces act on objects. The First Law is based on the idea in which motion state changes because of outer forces, the Second Law quantitatively describes and concludes the relation of force, mass, and acceleration, strongly grounded in the Third Law, which is based on the action and opposite reactions.