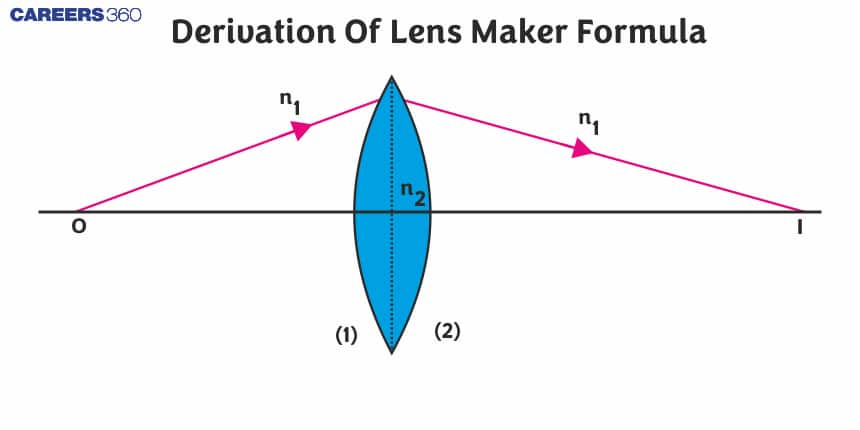
Derivation Of Lens Maker Formula

The refractive index and curvatures of lens surfaces relate the focal length with Lens Maker's formula. Its significance in designing lenses that achieve certain focal lengths is important to the optics industry. It is based on the ideas behind refraction at spherical surfaces and the geometry of thin lenses. The assumption is that they are all made from one type of material which has a different refractive index than air (the most common) or water (less frequently). This equation applies both convex and concave lenses helping understand how the curvature of these two shapes with several materials will affect image making.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Lens Maker Formula
2. What is a Thin Lens?
3. What is Focal length?
4. Derivation of Lens Maker’s Formula
5. Image Formation With a Thin Lens: Characteristics
6. Limitations of the Lens Maker’s Formula
7. Summary

Lens Maker Formula

For various optical equipment, lenses of varying focal lengths are utilized. The focal length of a lens is determined by the refractive index of the lens's material and the curvature radii of the two surfaces. The lens maker formula is derived here to help applicants better comprehend the subject. The lens maker formula is often used by lens manufacturers to create lenses with the appropriate focal length.

For spherical lenses, the lens equation or lens formula is an equation that links the focal length, image distance, and object distance.
Lens Formula $=1 / v-1 / u=1 / f$ is how it's written. where. $v$ is the image's distance from the lens, $u$ is the object distance and $f$ is the focal length.

If the relationship between a lens' focal length, the refractive index of its material, and the radii of curvature of its two surfaces is known as the lens maker's formula. Lens manufacturers utilize it to build lenses with a specific power from glass with a specific refractive index.

$\frac{1}{f}=(n-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)$

Recommended Topic Video

NCERT Physics Notes :

• NCERT Notes class 11 physics
• NCERT Notes class 12 physics
• NCERT Notes for all subject

What is a Thin Lens?

A thin lens is defined as one whose thickness is insignificant in comparison to its curvature radii. The thickness (t) is significantly lower than the two curvature radiii $R_1$ and $R_2$
The focal length, image distance, and object distance are all connected in the lens formula for concave and convex lenses. The formula $1 / \mathrm{f}=1 / \mathrm{v}+1 / \mathrm{u}$ can be used to establish this link.
The focal length of the lens is $f$, and the distance of the generated image from the lens' optical centre is $v$ in this equation. Finally, $u$ is the distance between an item and the optical centre of this lens. For convex lenses, this is the lens equation.

Also, read

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

There are two types of thin lenses

To create a thin lens formula, you must first understand the difference between converging and diverging lenses.

• Converging lenses allow light rays that are parallel to the optic axis to pass through and converge at a common point behind them. The focal point (f) or focus is the name given to this point.
• Diverging - These lenses have the opposite purpose as converging lenses. Light rays parallel to the optic axis travel through and diverge here. It creates an optical illusion by giving the impression that the lights are coming from the same source (f) in front of the lens.

Recommended Topic Video

What is Focal length?

The focal length of an optical system is the inverse of the system's optical power; it measures how strongly the system converges or diverges light. A system with a positive focal length converges light, while one with a negative focal length diverges light.

What is the Formula of the Focal Lens?

The formula $(1 / v)+(1 / u)=(1 / f)$ gives the focal length of a double convex lens, where $u$ is the distance between the object and the lens and $v$ is the distance between the image and the lens.

OR,

$
F=-R / 2
$
Where,
$F$ is the focal length, and
$R$ is the radius of curvature of the lens

Derivation of Lens Maker’s Formula

The lens maker formula is derived using the assumptions listed below

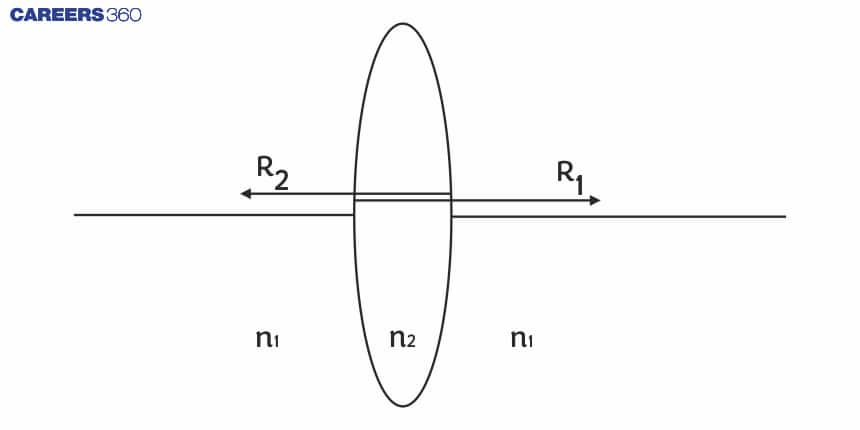
Consider the thin lens in the picture above, which has two refracting surfaces with curvature radii R₁ and R₂, respectively. Assume that the surrounding medium and the lens material have refractive indices of n₁ and n₂, respectively. The whole derivation of the lens maker formula is provided further below. We can say that, using the formula for refraction at a single spherical surface,

For the first surface,
$
\frac{n_2}{v_1}-\frac{r_1}{u}=\frac{n_2-r_1}{R_1} \ldots
$
For the second surface,

$
\frac{n_1}{v}-\frac{n_2}{v_1}=\frac{n_1-n_2}{R_2} \ldots
$
Now adding equation (1) and (2),

$
n 1 / v-n 1 / u=\left(n_2-n_1\right)\left[1 / R_1-1 / R_2\right]
$

on simplifying we get,

$
1 / v-1 / u=\left(n_2 / n_1-1\right)\left[1 / R_1-1 / R_2\right]
$
When $u=\infty$ and $v=f$

$
\frac{1}{f}=\left(\frac{n_2}{n_1}-1\right)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]
$

But also,
$
\frac{1}{v}-\frac{1}{u}=\frac{1}{f}
$
Therefore, we can say that,

$
\frac{1}{f}=(\mu-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)
$
Where $\mu$ is the material's refractive index.

Where μ is the material's refractive index.

This is the derivation of the lens maker formula. Examine the constraints of the lens maker's formula to have a better understanding of the lens maker's formula derivation.

Also read :

• NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
• NCERT Exemplar Class 12 Physics Solutions Chapter 9 Ray Optics and Optical Instruments
• NCERT notes Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

Image Formation With a Thin Lens: Characteristics

It's not enough to know the thin lens formula for convex lenses. The characteristics of a ray of light going through converging and diverging lenses must be understood.

1. On the opposite side, parallel rays going through converging lenses will intersect at point f.

2. Parallel rays seem to emerge from point f in front of diverging lenses.

3. The direction of light rays travelling through the centre of converging or diverging lenses does not change.

4. Light rays that enter a converging lens through its focal point always exit parallel to the lens's axis.

5. On the other side of a diverging lens, a light ray going towards the focal point will also emerge parallel to its axis.

A concave or divergent lens has a negative focal length. When the picture is generated on the side where the object is positioned, the image distance is also negative. The image is virtual in this case. A converging or convex lens, on the other hand, has a positive focal length.

Also, check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects

Limitations of the Lens Maker’s Formula

• The lens should not be thick so that the space between the 2 refracting surfaces can be small.
• The medium used on both sides of the lens should always be the same.

Summary

The Lens Maker's Formula relates the focal length of a lens to the refractive index of its material and the radii of curvature of its two surfaces. Derived from the principles of refraction, the formula is given by $\frac{1}{f}=(n-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)$, where $n$ is the refractive index of the lens material, and $R_1$ and $R_2$ are the radii of curvature of the lens surfaces. This formula is essential for designing lenses with specific focal lengths. However, it assumes a thin lens and equal media on both sides and does not account for spherical and chromatic aberrations, which can limit its accuracy in practical applications.