Spherical Mirrors

Imagine looking into a shiny, curved spoon. The curved surface creates a fascinating reflection that either enlarges or shrinks your image, depending on which side you are viewing. This is similar to how spherical mirrors work. Spherical mirrors are mirrors with curved surfaces that can either converge or diverge light. There are two types of spherical mirrors: concave and convex.

This Story also Contains

1. Spherical Mirror
2. Solved Examples Based on Spherical Mirrors
3. Summary

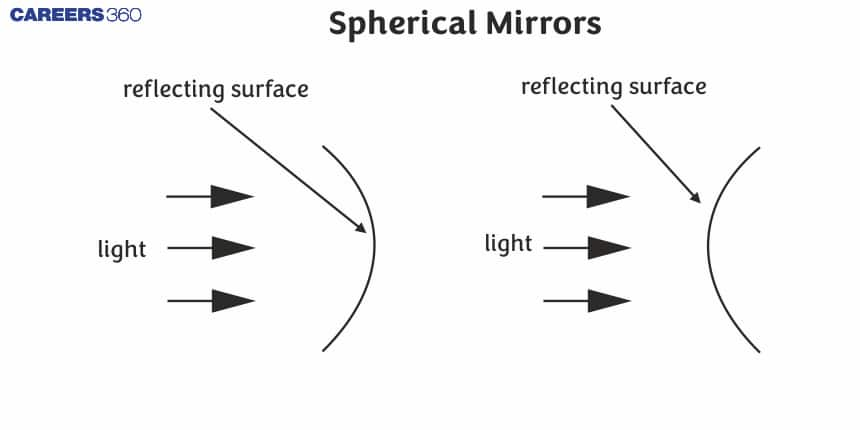
Concave mirrors, like the inside of a spoon, curve inward. They can focus light to a single point, making them useful in applications like telescopes, shaving mirrors, and headlights, where focused light or magnified images are required. Convex mirrors, like the back of a spoon, curve outward. They spread out light rays, providing a wider field of view, making them ideal for use in vehicle side mirrors and security mirrors in stores.

In this article, we are going to learn about spherical mirrors, some important technology and solved example on this concept of chapter optics.

Spherical Mirror

It is a part of a transparent hollow sphere whose surface is polished.

There are two types of spherical mirrors: concave, and convex.

In the above figure, A concave (left) and a convex (right) mirror is shown.

Some Important Terminology

• Centre of curvature (C)- The Centre of the sphere of which the mirror is a part is called the Centre of curvature.
• Pole (P)- The geometrical centre of the spherical reflecting surface.
• The radius of curvature (R)- The radius of the sphere of which the mirror is a part is called the radius of curvature.

or R= Distance between pole and centre of curvature

$\left(\right.$ Note $\left.\Rightarrow R_{\text {concave }}=-v e, \quad R_{\text {convex }}=+v e, R_{\text {plane }}=\infty\right)$

• Principle axis- A line passing through P and C is known as the Principle axis.
• Focus (F)- When a narrow beam of rays of light, parallel to the principal axis and close to it, is incident on the surface of a mirror, the reflected beam is found to coverage to or appears to diverge from a point on the principal axis. This point is called the focus.

or An image point on the principal axis for which the object is at $\infty$ is called the focus.

C, P, and F for a concave mirror are shown in the below figure.

• Focal Length (f)- It is the distance between the pole and the principal focus. For spherical mirrors, $f=\frac{R}{2}$

(i.e $\left.f_{\text {concarr }}=-v e, f_{\text {convex }}=+v e, f_{\text {plane }}=\infty\right)$

• Focal plane- A plane passing from focus and perpendicular to the principal axis.

Recommended Topic Video

Solved Examples Based on Spherical Mirrors

Example 1: A hemispherical glass body of radius 10 cm and refractive index 1.5 is silvered on its curved surface. A small air bubble is 6 cm below the flat surface inside it along the axis. The position of the image of the air bubble made by the mirror is seen :

1) 14 cm below the flat surface

2) 30 cm below the flat surface

3) 20 cm below the flat surface

4) 16 cm below the flat surface

Solution:

Relation between focal length and radius of curvature

$f=\frac{R}{2}$

wherein

R = Radius of curvature

This is valid only for smaller angles of incidence.

i.e.paraxial rays

Mirror Formula

$\frac{1}{v}+\frac{1}{u}=\frac{1}{f}$

wherein

$u=$ Object distance from pole of mirror.
$v=$ Image distance from pole of mirror.
$f=$ focal length of the mirror.

Relation between real depth and apparent depth -

$
\frac{n_i}{d}=\frac{n_r}{d^{\prime}}
$
wherein
$n_i=$ Refractive index of the medium of the incident.
$n_\tau=$ Refractive index of the medium of refraction.
$d=$ distance of the object.
$d^{\prime}=$ apparent depth
Given the radius of hemispherical glass $\mathrm{R}=10 \mathrm{~cm}$
$
\begin{aligned}
& \therefore \text { focal length } f=\frac{10}{2}=-5 \mathrm{~cm} \\
& u=(10-6)=-4 \mathrm{~cm}
\end{aligned}
$

By using the mirror formula
$
\frac{1}{v}+\frac{1}{u}=\frac{1}{f}=\frac{1}{v}+\frac{1}{-4}=\frac{1}{-5} \Rightarrow v=20 \mathrm{~cm}
$

Apparent height
$
h_a=h_r \frac{\mu_1}{\mu_2}=30 \times \frac{1}{1.5}=20 \mathrm{~cm}
$

below the flat surface.

Hence, the answer is option (3).

Example 2: You are asked to design a shaving mirror assuming that a person keeps it 10 cm from his face and views the magnified image of the face at the closest comfortable distance of 25 cm. The radius of curvature of the mirror would then be :

1) 30 cm

2) 24 cm

3) 60 cm

4) 28 cm

Solution:

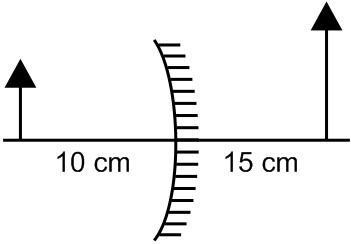
From question v = 15 cm, u = -10 cm

The radius of curvature R = 2f

Mirror formula $\frac{1}{v}+\frac{1}{u}=\frac{1}{f}=\frac{1}{15}+\frac{1}{(-10)}=\frac{1}{f}$

f = - 30 cm

$\therefore$ R= 2(-30) = - 60 cm

Hence, the answer is option (3).

Example 3: The geometrical centre of the spherical reflecting surface is called -

1) Centre of curvature

2) Pole

3) Principal focus

4) Geometrical focus

Solution:

Pole (P)- The geometrical centre of the spherical reflecting surface.

Represented by 'P' here

Hence, the answer is option (2).

Example 4: What will be the length of the focal point from the pole (cm), if the radius of curvature of the spherical mirror is 28 cm?

1) 56

2) 14

3) 42

4) 7

Solution:

Focal Length (f)- It is the distance between the pole and the principal focus. For spherical mirrors, $f=\frac{R}{2}$

So,

$f=\frac{28}{2}=14 \mathrm{~cm}$

Hence, the answer is the option (2).

Example 5: The focal length f is related to the radius of the curvature r of the spherical convex mirror by:

1) $f=+\frac{1}{2} r$
2) $f=-\frac{1}{2} r$
3) $f=r$
4) $f=-r$

Solution:

In the case of spherical mirrors, there are some sign conventions that we need to consider:-

1. All distances are measured from the pole of the mirror.

2. Distances measured in the direction of the incident ray are positive and the distances measured in the direction opposite to that of the incident rays are negative.

For a convex mirror, the focus is behind the mirror and is taken to positive which is in the direction of the incident ray.

$\therefore f=+\frac{r}{2}$

Hence, the answer is option (1).

Summary

Spherical mirrors are mirrors that are curvy in shape and include two types:i.e., concave and convex. Mirrors that cave inwards are referred to as concave mirrors. Based on an object’s position vis a vis the focal point of the mirror, light can be focused by these. Therefore it could be either a real or virtual image they form. Telescopes make use of them, as well as Headlights, and shaving mirrors just to mention a few examples. Contrarily, on the other hand, mirrors that bulge outwards are convex mirrors like those found on rear-view cars.