Electric Field Of A Dipole

Imagine holding two magnets close together, one with its north pole facing the south pole of the other. The space around these magnets is filled with an invisible force field, pulling or pushing depending on where you place another magnet nearby. In the world of electric charges, a similar setup is known as a dipole, which consists of two equal but opposite charges separated by a small distance.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Electric Field Intensity due to an Electric Dipole at a Point on the Axial Line
2. Electric Field Intensity due to an Electric Dipole at a Point on the Equatorial line
3. Solved Examples Based on Electric Dipole
4. Summary

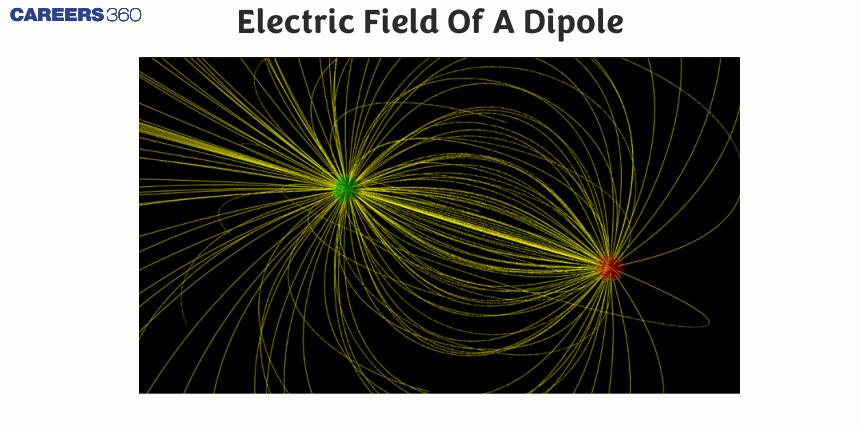
The electric field created by a dipole is unique because it’s not uniform; it varies in strength and direction depending on where you are relative to the dipole. This field plays a crucial role in many natural and technological phenomena, from the behaviour of molecules in chemistry to the functioning of antennas in communication systems. In this article, we’ll explore how the electric field of a dipole is structured, how it behaves at different points in space, and why it’s important in various applications.

Electric Field Intensity due to an Electric Dipole at a Point on the Axial Line

As shown in the above figure We want to find out the Electric Field Intensity due to an Electric Dipole at Point M which is on the axial line and at a distance r from the centre of a dipole.

Where $E_1$ and $E_2$ is the Electric Field Intensity at M due to $-q$ and $+q$ charges respectively.
The intensities $E_1$ and $E_2$ are along the same line but in opposite directions.

The intensities $E_1$ and $E_2$ are along the same line but in opposite directions. $◻$

$\begin{array}{rl}& E_1=\frac{kq}{(r+a{)}^2}\\ & E_2=\frac{kq}{(r-a{)}^2}\\ & E_{\text{net}}=E_2-E_1\\ & E_{\text{net}}=\frac{Kq}{(r-a{)}^2}-\frac{Kq}{(r+a{)}^2}=\left[\frac{4Kqar}{{(r^2-a^2)}^2}\right]\\ & \text{Using}P=q(2a)\\ & E_{\text{net}}=\left[\frac{2KPr}{{(r^2-a^2)}^2}\right]\end{array}$

For short/Ideal dipole (i.e r>>a)

then
${\overrightarrow{E}}_{net}=\frac{2K\overrightarrow{P}}{r^3}=\frac{2\overrightarrow{P}}{4\pi {ϵ}_0{r}^3}$ (This is the value of $E_{net}$ when the dipole is placed in the vacuum.)

If the dipole is placed in the medium having the permittivity as ${ϵ}_m$
Then
${\overrightarrow{E}}_{net}=\frac{2\overrightarrow{P}}{4\pi {ϵ}_m{r}^3}=\frac{2\overrightarrow{P}}{4\pi {ϵ}_0{ϵ}_r{r}^3}$

Note: The direction of the electric field E is in the direction of $\overrightarrow{P}$.

i.e. Angle between ${\mathrm{E}}_{\mathrm{axi}}$ and $\overrightarrow{P}$ is $0^0$.

Electric Field Intensity due to an Electric Dipole at a Point on the Equatorial line

As shown in the above figure We want to find out the Electric Field Intensity due to an Electric Dipole at Point M which is on the Equatorial line and at a distance r from the centre of a dipole.

Where $E_1$ and $E_2$ is the Electric Field Intensity at M due to $-q$ and $+q$ charges respectively.
$\begin{array}{rl}& \left|\overrightarrow{E_1}\right|=\frac{1}{4\pi {ϵ}_0}\ast \frac{q}{r^2+a^2}\\ & \left|\overrightarrow{E_2}\right|=\frac{1}{4\pi {ϵ}_0}\ast \frac{q}{r^2+a^2}\\ & \text{So}\left|\overrightarrow{E_1}\right|=\left|\overrightarrow{E_2}\right|=|\overrightarrow{E}|\\ & |\overrightarrow{E}|=2\left|E_1\right|\cos \theta \\ & =\frac{2}{4\pi {ϵ}_0}\cdot \frac{q}{(r^2+a^2)}\cos \theta \\ & =\frac{2}{4\pi {ϵ}_0}\cdot \frac{q}{(r^2+a^2)}\frac{a}{\sqrt{r^2+a^2}}\\ & =\frac{q\times 2a}{4\pi {ϵ}_0{(r^2+a^2)}^{3/2}}\\ & \end{array}$

Using $P=q(2a)$
$\therefore \overrightarrow{E}=\frac{-\overrightarrow{P}}{4\pi {ϵ}_0{(r^2+a^2)}^{3/2}}$

And

then
${\overrightarrow{E}}_{\text{net}}=\frac{-K\overrightarrow{P}}{r^3}=\frac{-\overrightarrow{P}}{4\pi {ϵ}_0{r}^3}$
(This is the value of $E_{\text{net}}$ when the dipole is placed in the vacuum.)

If the dipole is placed in the medium having the permittivity as ${ϵ}_m$
$\text{Then}{\overrightarrow{E}}_{\text{net}}=\frac{-\overrightarrow{P}}{4\pi {ϵ}_m{r}^3}=\frac{-\overrightarrow{P}}{4\pi {ϵ}_0{ϵ}_r{r}^3}$

Note: Here the direction of the electric field E is opposite to the direction of $\overrightarrow{P}$

i.e. Angle between ${\mathrm{E}}_{\text{enui}}$ and $\overrightarrow{P}$ is ${180}^{\circ }$

As shown in the above figure We want to find out the Electric Field Intensity due to an Electric Dipole at Point M which at a distance r from the center of a dipole and making an angle $\theta$ with the axial line.

From the figure, M is at the axial line of dipole having dipole moment as $P\cos \theta$ and M is at the Equatorial line of dipole having dipole moment as $P\sin \theta$

if $r>>a$
$\begin{array}{rl}& \text{Then}{E}_a=\frac{1}{4\pi {\epsilon }_0}\times \frac{2P\cos \theta }{r^3}\text{and}{E}_{\perp }=\frac{1}{4\pi {\epsilon }_0}\times \frac{P\sin \theta }{r^3}\\ & \left|{\overrightarrow{E}}_{net}\right|=\sqrt{E_a^2+E_{\perp }^2}\\ & \left|{\overrightarrow{E}}_{net}\right|=\sqrt{{\left\{\frac{2KP\cos \theta }{r^3}\right\}}^2+{\left\{\frac{KP\sin \theta }{r^3}\right\}}^2}\\ & =\sqrt{{\frac{KP}{(r^3})}^2\{4{\cos }^2\theta +{\sin }^2\theta \}}\\ & =\frac{KP}{r^3}\sqrt{1+3{\cos }^2\theta }\\ & \end{array}$

Let's make an angle $\alpha$ with $E_a$
then
$\tan \alpha =\frac{E_{\perp }}{E_a}=\frac{\sin \theta }{2\cos \theta }=\frac{1}{2}\tan \theta$

Note- The above results are valid only for short/Ideal dipole.

Solved Examples Based on Electric Dipole

Example 1: The potential at a point due to an electric dipole will be maximum and minimum when the angles between the axis of the dipole and the line joining the point to the dipole are respectively:

1) ${90}^{\circ }$ and ${180}^{\circ }$
2) $0^{\circ }$ and ${90}^{\circ }$
3) ${90}^{\circ }$ and ${.0}^{\circ }$
4) $0^{\circ }$ and ${180}^{\circ }$

Solution:

At equatorial Point

$E_{\text{equi}}=\frac{kP}{{(r^2+l^2)}^{\frac{3}{2}}}$

If $r\gg$ I
$\begin{array}{rl}& E_{\text{equi}}=\frac{1}{4\pi {\epsilon }_0}\frac{P}{r^3}\\ & V_{\text{equi}}=0\end{array}$
wherein
The angle between ${\mathrm{E}}_{\text{axial}}$ and P is ${180}^{\circ }$.
$V=\frac{p\cos \theta }{r^2}\text{..if}\theta =0^{\circ }..\text{then..}{V}_a=max$

Hence, the answer is the option(4).

Example 2: An electric dipole moment $\overrightarrow{p}=(-\hat{i}-3\hat{j}+2\hat{k})\times {10}^{-29}\mathrm{Cm}$ is at the origin $(0,0,0)$. The electric field due to this dipole at $\overrightarrow{r}=+\hat{i}+3\hat{j}+5\hat{k}$ (note that $\overrightarrow{r}\cdot \overrightarrow{p}=0$ ) is parallel to:

1) $+\hat{i}-3\hat{j}-2\hat{k}$
2) $-\hat{i}-3\hat{j}+2\hat{k}$
3) $+\hat{i}+3\hat{j}-2\hat{k}$
4) $-\hat{i}+3\hat{j}-2\hat{k}$

Solution:

$\overrightarrow{p}\cdot \overrightarrow{r}=0$

E must be antiparallel to $p$
$\begin{array}{rl}& \overrightarrow{E}=-\lambda \overrightarrow{p}\\ & \overrightarrow{A}=ai+bj+ck\\ & \Rightarrow \frac{a}{\lambda }=\frac{b}{3\lambda }=\frac{-c}{2\lambda }=k\\ & \Rightarrow A=\lambda (i+3j-2k)\end{array}$

Hence, the answer is the option (3).

Example 3: If the magnitude of the intensity of the electric field at a distance x on the axial line and, at a distance y on the equatorial line on a given dipole are equal, then x:y is

1) $1:1$
2) $1:\sqrt{2}$
3) $1:2$
4) $\sqrt[3]{2}:1$

Solution:

Given that the magnitudes of the electric field at a distance \( x \) on the axial line and at a distance \( y \) on the equatorial line of a dipole are equal, we need to find the ratio \( x:y \).

The electric field due to a dipole at a point on the axial line is given by:

$E_{\text{axial}}=\frac{2kp}{x^3}$

where \( k \) is the electrostatic constant, \( p \) is the dipole moment, and \( x \) is the distance from the dipole.

The electric field due to a dipole at a point on the equatorial line is given by:

$E_{\text{equatorial}}=\frac{kp}{y^3}$

Given that these magnitudes are equal, we have:

$\frac{2kp}{x^3}=\frac{kp}{y^3}$

We can cancel out \( kp \) from both sides:

$\frac{2}{x^3}=\frac{1}{y^3}$

Taking the cube root on both sides:

$\sqrt[3]{2}=\frac{y}{x}$

Therefore, the ratio \( x:y \) is:

$x:y=\frac{1}{\sqrt[3]{2}}:1=\sqrt[3]{2}:1$

The correct answer is:

$\boxed{{\displaystyle \sqrt[3]{2}:1}}$

Example 4: The electric field at a point on the equatorial line of a dipole and the direction of the dipole moment

1) Will be parallel

2) Will be in the opposite direction

3) Will be perpendicular

4) Are not related

Solution:

The direction of the electric field at the equatorial point will be in the opposite direction, as that of the direction of the dipole moment.

$\therefore \overrightarrow{E}=\frac{-\overrightarrow{p}}{4\pi {ϵ}_0{(r^2+a^2)}^{3/2}}$

The angle between ${\mathrm{E}}_{\text{equi}}$ and $\overrightarrow{p}$ is ${180}^{\circ }$.

Hence, the answer is the option 2.

Example 5: Charge $-q$ and $+q$ located at A and B, respectively, constitute an electric dipole. Distance $AB=2a,O$ is the midpoint of the dipole and $OP$ is perpendicular to $AB$. $A$ charge $Q$ is placed at $P$ where $OP=y$ and $y>2a$. The charge $Q$ experience an electrostatic force $F$. If $Q$ is now moved along the equational line to $P^{\prime }$ such that $O{P}^{\prime }=\left(\frac{y}{3}\right)$, the force on Q will be close to: $(\frac{y}{3}\gg >2a)$

1) 9F

2) 27F

3) F/3

4) 3F

Solution:

The electric field of the equatorial plane of the dipole $=\frac{-k\overrightarrow{p}}{r^3}$
At $\mathrm{P},\mathrm{F}=\frac{-K\overrightarrow{P}Q}{r^3}$

At $P^{\prime }$
$F^{\prime }=\frac{-K\overrightarrow{P}Q}{{\frac{r}{3}}^3}=27F$

Hence, the answer is option (2).

Summary

The electric dipole is made up of two same charges which are oppositely and a small distance at that point separates them. It therefore has a property known as its dipole moment; this is a vector which points from the negative end of the charge to the positive end of the charge across a separation. A dipole which was at rest in space will develop torque under the influence of external electric field forces applied to it with the aim of making its axes align with these lines.