Potential Due To Hollow Conductiong, Solid Conducting, Hollow Non Conducting

Edited By Vishal kumar | Updated on Sep 17, 2024 01:15 AM IST

Wonder what happens to the electric potential around variously charged objects? This may be a hollow conducting sphere, a solid conducting sphere, or even a hollow non-conducting sphere since each of these geometries does something different with electric charges. The concepts learned from studying electric potentials developed for such figures make up the foundation necessary to aid the understanding of a lot of principal ideas in electrostatics, of very critical significance in the design and analysis of electronic devices and systems.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

Electric Potential due to Hollow conducting, Hollow non-conducting, Solid Conducting Sphere-
Electric Potential due to Uniformly Charged Non conducting Sphere
Solved Examples Based On Potential Due To Hollow Conducting, Solid Conducting, Hollow Non-Conducting

Further, we discuss that the article, Potential Due To Hollow Conduction, Solid Conducting, and Hollow Non-conducting is important for board exams and comparative exams. This concept is in the class 12th electrostatic chapter. Questions asked from these competitive exams like the JEE Main, NEET, and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of fourteen questions have been asked on this concept. And for NEET four questions were asked from this concept.

Electric Potential due to Hollow conducting, Hollow non-conducting, Solid Conducting Sphere-

In the case of Hollow conducting, Hollow non-conducting, Solid conducting Spheres charges always reside on the surface of the sphere.

If the charge on a conducting sphere of radius R is Q. we want to find V at point P at distance r from the centre of the sphere.

Outside the sphere (P lies outside the sphere. I.e r>R)

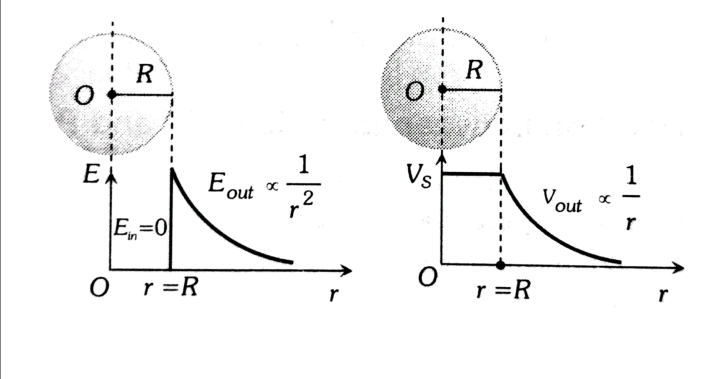
$\dpi{100} E_{out}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{r^{2}}=\frac{\sigma R^{2}}{\epsilon _{0}r^{2}}$

$V(r)=-\int_{r=\infty}^{r=r} \vec{E}.d \vec{r} =\frac{1}{4 \pi \varepsilon_{0}} \frac{\vec{Q}}{r}$

Inside the sphere (P lies inside the sphere. I.e r<R )

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

$E_{in}=0$

$V_{in}=constant$ and it is given as

$\boldsymbol{V}(\boldsymbol{r})=-\int_{r=\infty}^{r=r} \overrightarrow{\boldsymbol{E}} . d \vec{r} =-\int_{\infty}^{R} \boldsymbol{E}_{r}(d \boldsymbol{r})-\int_{R}^{r} \boldsymbol{E}_{r}(\boldsymbol{d} \boldsymbol{r})=\frac{1}{4 \pi \boldsymbol{\varepsilon}_{0}} *\frac{\boldsymbol{q}}{ {\boldsymbol{R}}}+0 \\ \\ \Rightarrow V(r)=\frac{1}{4 \pi \boldsymbol{\varepsilon}_{0}} *\frac{\boldsymbol{q}}{ {\boldsymbol{R}}}$

At the surface of Sphere (I.e at r=R)

$E_{s}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{R^{2}}=\frac{\sigma }{\epsilon _{0}}$

$V_{s}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{R}=\frac{\sigma R}{\epsilon _{0}}$

The graph between (E vs r) and (V vs r) is given below

Electric Potential due to Uniformly Charged Non conducting Sphere

Suppose charge Q is uniformly distributed in the volume of a non-conducting sphere of Radius R.

And we want to find V at point P at distance r from the center of the sphere.

Outside the sphere (P lies outside the sphere. I.e r>R)

$E_{out}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{r^{2}}$ $V_{out}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{r}$

$E_{out}=\frac{\rho R^{3}}{3 \epsilon _{0}r^{2}}$ $V_{out}=\frac{\rho R^{3}}{3 \epsilon _{0}r}$

Inside the sphere (P lies inside the sphere. I.e r<R )

$E_{in}=\frac{1}{4\pi \epsilon _{0}}\frac{Qr}{R^{3}}$ $\dpi{100} V_{in}=\frac{Q}{4\pi \epsilon _{0}}*\frac{3R^{2}-r^{2}}{2R^{3}}$

$\dpi{100} E_{in}=\frac{\rho r}{3 \epsilon _{0}}$ $V_{in}=\frac{\rho \left ( 3R^{2}-r^{2} \right )}{6 \epsilon _{0}}$

At the surface of Sphere (I.e at r=R)

$E_{s}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{R^{2}}$ $V_{s}=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{R}$

$\dpi{100} E_{s}=\frac{\rho R}{3 \epsilon _{0}}$ $V_{s}=\frac{\rho R^{2}}{3 \epsilon _{0}}$

Note - If P lies at the centre of the uniformly charged non-conducting sphere (I.e at r=0)

$V_{centre}=\frac{3}{2}\times \frac{1}{4\pi \epsilon _{0}}\frac{Q}{R}=\frac{3}{2}V_{s}$

i.e $\dpi{100} V_{c}> V_{s}$

The graph between (E vs r) and (V vs r) is given below

Solved Examples Based On Potential Due To Hollow Conducting, Solid Conducting, Hollow Non-Conducting

Example 1: A solid conducting sphere having a charge Q is surrounded by an uncharged concentric conducting hollow spherical shell. Let the potential difference between the surface of the solid sphere and that of the outer surface of the hollow shell be V. If the shell is now given a charge of –3Q, the new potential difference between the same two surfaces is

1) V

2)2V

3)4V

4)-2V

Solution:

The electric field in between the shell and sphere is $\\ E \pi x^{2}=\frac{Q_{e n}}{\epsilon_{0}}=\frac{Q}{\epsilon_{0}} \text{(using Gauss's law)} \\ E=\frac{Q}{4 \pi \varepsilon_{0} x^{2}}$

The potential difference between the shells is

$\mathrm{dV}=\mathrm{V}_{\mathrm{r}}-\mathrm{V}_{\mathrm{R}}=\int_{\mathrm{r}}^{\mathrm{R}} \mathrm{Edx}=\int_{r}^{R} \frac{Q}{4 \pi \epsilon_{0} \mathrm{x}^{2}} d x=\frac{Q}{4 \pi \epsilon_{0}}(1 / r-1 / R)$

Thus, $\mathrm{V}=\frac{\mathrm{Q}}{4 \pi \varepsilon_{0}}(1 / \mathrm{r}-1 / \mathrm{R})$

As the potential difference between a solid sphere and a hollow shell depends on the radii of two spheres and the charge on the inner sphere, Since the two values have not changed, the potential difference does not change. Hence the potential difference remains V.

Example 2: A spherical shell of radius R = 1.5 cm has q = 20 $\mu C$ uniformly distributed over it. The force exerted by one half over the other half is

1)0

2)10^-2 N

3)500 N

4)2000 N

Solution:

$\\*E=\frac{\sigma }{2\epsilon_0}\Rightarrow F=E.dQ=\frac{\sigma dA\sigma }{2\epsilon_0}\\*P=\frac{F}{dA}=\frac{\sigma ^{2}}{2\epsilon_0}\\*F=P\pi R^{2}=\frac{\sigma ^{2}}{2\epsilon_0}.\pi R^{2}=\frac{Q^{2}}{32\pi \epsilon_ 0R^{2}}=2000N$

Example 3: A conducting sphere of radius R is given a charge Q. Consider three points B at the surface, A at the centre and C at a distance R/2 from the centre. The electric potential at these points is such that

1) $V_{A}=V_{B}=V_{C}$

2) $V_{A}=V_{B}\neq V_{C}$

3) $V_{A}\neq V_{B}\neq V_{C}$

4) $V_{A}\neq V_{B}= V_{C}$

Solution:

As we learned

Inside the sphere (P lies inside the sphere) -

$E_{in}=0$

$V_{in}=constant$

- wherein

The potential inside a conductor is always constant and equal to the potential at the surface.

Example 4: Which of the following is correct

1)for charged non-conducting sphere $V_{centre}>V_{surface}>V_{out}$

2)for charged non-conducting sphere $V_{centre}\leq V_{surface}>V_{out}$

3)for charged non-conducting sphere $V_{centre}> V_{surface}= V_{out}$

4)for charged non-conducting sphere $V_{centre}> V_{surface}\equiv V_{out}$

Solution:

As we learned

Potential - If P lies at the centre of the uniformly charged non-conducting sphere -

$V_{centre}=\frac{3}{2}\times \frac{1}{4\pi \epsilon _{0}}\frac{Q}{R}=\frac{3}{2}V_{s}$

i.e $\dpi{100} V_{c}> V_{s}$

$V_{centre}=\frac{3}{2}\times \frac{1}{4\pi \varepsilon _{0}}\cdot \frac{Q}{R}=\frac{3}{2}V_{s}$

Example 5: A charge Q is distributed over two concentric conducting thin spherical shells radii r and R (R>r). If the surface charge densities on the two shells are equal, the electric potential at the common centre is ;

1) $\frac{1}{4\pi \epsilon _0}\frac{\left ( 2R+r \right )}{\left ( R^2+r^2 \right )}Q$

2) $\frac{1}{4\pi \epsilon _0}\frac{\left (R+r \right )}{2\left ( R^2+r^2 \right )}Q$

3) $\frac{1}{4\pi \epsilon _0}\frac{\left (R+r \right )}{\left ( R^2+r^2 \right )}Q$
4) $\frac{1}{4\pi \epsilon _0}\frac{\left (R+2r \right )Q}{2\left ( R^2+r^2 \right )}$

Solution:

$\begin{array}{l} \mathrm{Q}_{1}=\sigma 4 \pi \mathrm{r}^{2} \\ \mathrm{Q}_{2}=\sigma 4 \pi \mathrm{R}^{2} \end{array}$

Where ${Q}_{1}$ = charge on the inner shell and ${Q}_{2}$ = charge on the outer shell

and $Q={Q}_{1}+{Q}_{2}$

$\begin{array}{l} Q=\sigma 4 \pi\left(r^{2}+R^{2}\right) \\ \sigma=\frac{Q}{4 \pi\left(r^{2}+R^{2}\right)} \end{array}$

$\begin{array}{l} \mathrm{V}_{\mathrm{C}}=\frac{\mathrm{KQ}_{1}}{\mathrm{r}}+\frac{\mathrm{KQ}_{2}}{\mathrm{R}} =\frac{\mathrm{K} \sigma 4 \pi \mathrm{r}^{2}}{\mathrm{r}}+\frac{\mathrm{K} \sigma 4 \pi \mathrm{R}^{2}}{\mathrm{R}} =\mathrm{K} \sigma 4 \pi(\mathrm{r}+\mathrm{R}) \\ \\ V_C=\frac{\mathrm{KQ} 4 \pi(\mathrm{r}+\mathrm{R})}{4 \pi\left(\mathrm{r}^{2}+\mathrm{R}^{2}\right)} =\frac{\mathrm{KQ}(\mathrm{r}+\mathrm{R})}{\left(\mathrm{r}^{2}+\mathrm{R}^{2}\right)} =\frac{\mathrm{Q}(\mathrm{r}+\mathrm{R})}{4\pi\epsilon _0\left(\mathrm{r}^{2}+\mathrm{R}^{2}\right)}\end{array}$

Summary:
Because material properties differ, and charges are distributed differently in these cases, the electric potential will become different for a hollow conducting, solid conducting, and hollow non-conducting sphere. In the case of a hollow conducting sphere, charges reside on the surface and hence produce a uniform potential inside. For a solid conducting sphere, the charges will distribute on the surface and produce uniform potential inside. In these instances, however, the potential distributions turn out to be different in the case of a hollow non-conducting sphere, for it does not conduct charges. Getting a grip on these differences is very crucial in applications in electronics and physics.