Electric Field Of Charged Disk

The electric field of a uniformly charged disk is a fundamental problem in electrostatics, frequently encountered in physics. A charged disk generates an electric field that varies with distance from its surface, and its distribution of charge plays a crucial role in determining the field's characteristics. The field is typically analyzed in the plane perpendicular to the disk's surface, with special attention to the axis passing through its centre.

This Story also Contains

1. Electric Field Due to Uniformly Charged Disk
2. Some Solved Examples:
3. Summary:

Electric Field Due to Uniformly Charged Disk

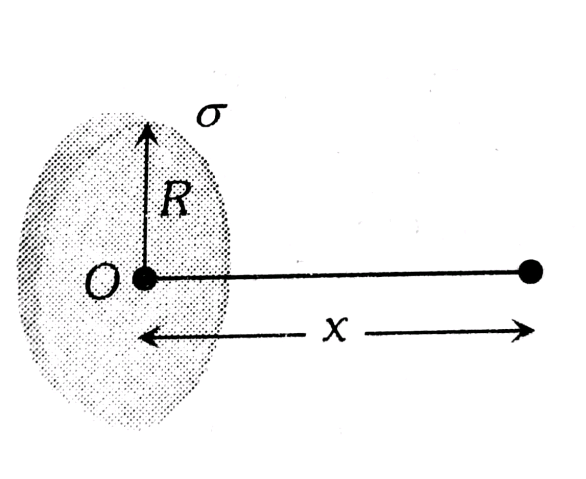
Let us take a disk of radius R with a uniform positive surface charge density (charge per unit area) $\sigma$. Our aim is to find an electric field at a point on the axis of the disk at a distance x from its centre.

From the figure, we can see that we have taken a typical ring that has charge $dQ$, inner radius $r$ and outer radius $r+dr$. Its area $dA$

$d{E}_x=\frac{1}{4\pi {\epsilon }_0}\frac{(2\pi \sigma rdr)x}{{(x^2+r^2)}^{3/2}}$
If we integrate from 0 to $R$, we will get the total field -

$E_x=\int d{E}_x={\int }_0^{R}d{E}_x={\int }_0^R\frac{1}{4\pi {\epsilon }_0}\frac{(2\pi \sigma rdr)x}{{(x^2+r^2)}^{3/2}}$
Here, ' $x$ ' is constant and 'r' is the variable. After integration, we get -

$E_x=\frac{\sigma x}{2{\epsilon }_0}[-\frac{1}{\sqrt{x^2+R^2}}+\frac{1}{x}]=\frac{\sigma }{2{\epsilon }_0}[1-\frac{x}{\sqrt{x^2+R^2}}]$
As this disc is symmetric to the x -axis, the field in the rest of the component is zero i.e., $E_y=E_z=0$

Special case -
1) When $R>>x$, then $E_x=\frac{\sigma }{2{\epsilon }_0}$ Note that this equation is independent of ' $x$ '
2) When $x\to 0$ (i.e very near to the disc), then $E_x=\frac{\sigma }{2{\epsilon }_0}$

Recommended Topic Video

Some Solved Examples:

Example 1: A thin disc of radius b=2a has a concentric hole of radius 'a' in it (see figure). It carries a uniform surface charge $'\sigma '$on it. If the electric field on its axis at height' h ' (h<<a) from its centre is given as 'Ch' then value of 'C' is :

$\begin{array}{rl}& \frac{\sigma }{\frac{\sigma }{a{ϵ}_0}}\\ & \frac{\sigma }{2{)}^{2a{ϵ}_0}}\end{array}$

3) $\frac{\sigma }{4a{ϵ}_0}$

$\frac{\sigma }{8{)}^{8a{ϵ}_0}}$
Solution:

As we discussed in

Uniformly charged disc -

$\begin{array}{rl}& E=\frac{\sigma }{2{ϵ}_0}[1-\frac{x}{{(x^2+R^2)}^{\frac{1}{2}}}]\\ & V=\frac{\sigma }{2{ϵ}_0}[\sqrt{x^2+R^2}-x]\end{array}$
- wherein

Electric Field due to complete disc $(R=2a)$ at distance $x$

$\begin{array}{rl}& E_1=\frac{\sigma }{2{ϵ}_o}[1-\frac{x}{{(R^2+x^2)}^{\frac{1}{2}}}][h=x;2a=R]\\ & E_1=\frac{\sigma }{2{ϵ}_o}[1-\frac{h}{{(4a^2+h^2)}^{\frac{1}{2}}}]=\frac{\sigma }{2{ϵ}_o}[1-\frac{h}{2a}]\end{array}$
Similarly, the electric field due to disc $(R=a)$

$E_2=\frac{\sigma }{2{ϵ}_o}[1-\frac{h}{a}]$
Now $E=E_1-E_2=\frac{\sigma }{2{ϵ}_o}[1-\frac{h}{2a}]-\frac{\sigma }{2{ϵ}_o}[1-\frac{h}{a}]=\frac{\sigma h}{4{ϵ}_{o}a}$
Hence $C=\frac{\sigma }{4{ϵ}_{o}a}$

Example 2: What will be the electric field due to a uniformly charged disc At a distance $x$ from centre $O$ on its axis if $X\to 0$

$\begin{array}{rl}E& =\frac{\sigma }{4{\epsilon }_0}\\ E& \simeq \frac{\sigma }{2{\epsilon }_0}\\ E& =\frac{2K\lambda }{R}=\frac{Q}{2{\pi }^2{\epsilon }_0{R}^2}\end{array}$

4)0

Solution:
As we learned
Uniformly charged disc -

$\begin{array}{rl}& \text{If}x\to 0\\ & E\simeq \frac{\sigma }{2{ϵ}_0}\end{array}$

wherein

i.e. Point situated near the disc it behaves as an infinite sheet of charge.

$E=\frac{\sigma }{2{\epsilon }_0}[1-\frac{x}{\sqrt{x^2+R^2}}]\text{Putx}=0$

Example 3 The surface charge density of a thin charged disc of radius R is $\sigma .$ The value of the electric field at the centre of the disc is $\frac{\sigma }{2{ϵ}_0\underset{―}{\underset{―}{y}}}$ With respect to the field at the centre, the electric field along the axis at a distance R from the centre of the disc :
1)reduces by $70.7\mathrm{\%}$
2)reduces by $29.3\mathrm{\%}$
3)reduces by $9.7\mathrm{\%}$
4)reduces by $14.6\mathrm{\%}$

Solution:
Electric field intensity at the centre of the disc

$\Rightarrow \mathrm{E}=\frac{\sigma }{2{ϵ}_0}(\text{given})$
Electric field along the axis at any distance $x$ from the centre of the disc

${\mathrm{E}}^{\prime }=\frac{\sigma }{2{ϵ}_0}(1-\frac{\mathrm{x}}{\sqrt{{\mathrm{x}}^2-{\mathrm{R}}^2}})$
From question, $x=R$ (radius of disc)

$\therefore {\mathrm{E}}^{\prime }=\frac{\sigma }{2{ϵ}_0}(1-\frac{\mathrm{R}}{\sqrt{{\mathrm{R}}^2+{\mathrm{R}}^2}})=\frac{\sigma }{2{ϵ}_0}\left(\frac{\sqrt{2}\mathrm{R}-\mathrm{R}}{\sqrt{2}\mathrm{R}}\right)=\frac{4}{14}\mathrm{E}$
So reduction in the value of electric field

$=\frac{(\mathrm{E}-\frac{4}{14}\mathrm{E})\times 100}{\mathrm{E}}=\frac{1000}{14}\mathrm{\%}=70.7\mathrm{\%}$

Example 4:Find out the surface charge density at the intersection of point $\mathrm{x}=3\mathrm{m}$ plane and the x -axis in the region of uniform line charge of $8\mathrm{nC}/\mathrm{m}$ along the z -axis in free space.
1) $47.88\mathrm{C}/\mathrm{m}$
2) $0.424\mathrm{nC}{\mathrm{m}}^{-2}$
3) $0.07\mathrm{nC}{\mathrm{m}}^{-2}$
4) $4.0\mathrm{nC}{\mathrm{m}}^{-2}$

Solution:
Electric field due to uniformly charged rod- $E=\frac{2K\lambda }{r}$

Electric field due to uniformly charged disk-

$\begin{array}{rl}& E=\frac{\sigma }{2{\epsilon }_0}\\ & \frac{2\mathrm{K}\lambda }{\mathrm{r}}=\frac{\sigma }{{\epsilon }_0}\\ & \sigma =\frac{2K\lambda {\epsilon }_0}{r}=\frac{\lambda }{2\pi r}=\frac{8\times {10}^{-9}}{2\pi \times 3}\\ & \sigma =0.424\times {10}^{-9}\frac{\mathrm{C}}{{\mathrm{m}}^2}\end{array}$

Summary:

To compute the electric field at a point along the axis of a uniformly charged disk, the disk is treated as a series of infinitesimal rings of charge. Each ring contributes to the net electric field, with its components integrated to find the total field. For a point close to the disk, the field behaves like that of a charged plane, while at far distances, it resembles the field of a point charge. The formula derived depends on the radius of the disk, surface charge density, and the distance from the point of interest to the disk’s centre.