Equation Of Path Of A Projectile

The equation of the path of a projectile describes the curved trajectory followed by an object that is launched into the air under the influence of gravity, assuming negligible air resistance. This concept is not just confined to textbooks but is widely observable in real life. Whether it's the arc of a basketball thrown towards a hoop, the flight of a soccer ball after being kicked, or even the water flowing out of a fountain, all these motions can be modelled using the projectile motion equation. Understanding this equation allows us to predict the path of any object thrown or projected, which is essential in fields like sports, engineering, and even space exploration. It helps in optimizing the angle and speed of launch to achieve the desired target, showcasing the relevance of this mathematical principle in everyday activities and professional practices.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Projectile Motion
2. Equation of Path of a Projectile
3. Solved Question Besed On Equation Of Path Of A Projectile
4. Summary

Projectile Motion

Two-dimensional motions under the action of the uniform force are called projectile motion.

E.g- A javelin thrown by an athlete

Projectile Projected at an angle

Initial Velocity- u

Horizontal component $=u_x=u\cos \theta$
Vertical component $=u_y=u\sin \theta$
Final velocity $=\mathrm{V}$
Horizontal component $=V_x=u\cos \theta$
Vertical component $=V_y=u\sin \theta -g.t$

So,

$V=\sqrt{V_x^2+V_y^2}$

Displacement = S

Horizontal component $=S_x=u\cos \theta .t$
Vertical component $=S_y=u\sin \theta \cdot t-\frac{1}{2}\cdot g\cdot t^2$

and, $S=\sqrt{S_x^2+S_y^2}$
Acceleration $=\mathrm{a}$
Horizontal component $=0$
Vertical component $=-g$
So, $a=-g$

Parameters In Projectile Motion

1) Maximum Height -

Maximum vertical distance attained by a projectile during its journey.

Formula,

$H=\frac{U^2{\sin }^2\theta }{2g}$

When the velocity of the projectile increases n time then the Maximum height is increased by a factor of $n^2$

Special Case: If U is doubled, H becomes four times provided $\theta \mathrm{\&}\mathrm{g}$ is constant.

2) Time of Flight -

Time for which projectile remains in the air above the horizontal plane.

Formula,

$T=\frac{2u\sin \theta }{g}$

Time of ascent $=t_a=\frac{T}{2}$

Time of descent $=t_d=\frac{T}{2}$

Notes:

• When the velocity of the projectile increases n time then the Time of ascent becomes n times.
• When the velocity of the projectile increases n time then the Time of descent becomes n times.
• When the velocity of the projectile increases n time then the time of flight becomes n times.

3) Horizontal Range

Horizontal distance travelled by a projectile from the point of the projectile to the point on the ground where it hits.

Formula,

$R=\frac{u^2\sin 2\theta }{g}$

The special case of horizontal range:

• For max horizontal range.

$\begin{array}{rl}\theta & ={45}^0\\ R_{max}& =\frac{u^2\sin 2(45)}{g}=\frac{u^2\times 1}{g}=\frac{u^2}{g}\end{array}$

• Range remains the same whether the projectile is thrown at an $\text{angle}\theta \text{with the horizontal or at an angle}\theta \text{with vertical}(90-\theta )$ with horizontal.
• When the velocity of the projectile increases n time then the horizontal range is increased by a factor of $n^2$
• When the horizontal range is n times the maximum height then,

$\tan \theta =\frac{4}{n}$

Equation of Path of a Projectile

$y=x\tan \theta -\frac{g{x}^2}{2u^2{\cos }^2\theta }$
or-
$y=x\tan \theta (1-\frac{x}{R})$

Where R is the horizontal range of the projectile.

It is the equation of the parabola, So the trajectory/path of the projectile is

parabolic in nature

$g\to$ Acceleration due to gravity
$u\to$ initial velocity
$\theta =$ Angle of projection

Recommended Topic Video

Solved Question Besed On Equation Of Path Of A Projectile

Example 1: The trajectory of a projectile near the surface of the earth is given as $y=2x-9x^2$. If it were launched at an angle ${\theta }_0$ with speed $v_0$ then $(g=10{\mathrm{ms}}^{-2})$ :

1) ${\theta }_0={\sin }^{-1}\left(\frac{2}{\sqrt{5}}\right)$ and $v_0=\frac{3}{5}m{s}^{-1}$
2) ${\theta }_0={\cos }^{-1}\left(\frac{2}{\sqrt{5}}\right)$ and $v_0=\frac{3}{5}m{s}^{-1}$
3) ${\theta }_0={\cos }^{-1}\left(\frac{1}{\sqrt{5}}\right)$ and $v_0=\frac{5}{3}m{s}^{-1}$
4) ${\theta }_0={\sin }^{-1}\left(\frac{1}{\sqrt{5}}\right)$ and $v_0=\frac{5}{3}m{s}^{-1}$

Solution:

Given :
$y=2x-9x^2$

The standard equation of trajectory for a projectile
$y=x\tan {\theta }_0-\frac{g{x}^2}{2v_0^2{\cos }^2{\theta }_0}$

On comparing Eq. (1) and (2)
$\begin{array}{rl}& \tan {\theta }_0=2\\ & \Rightarrow {\theta }_0={\sin }^{-1}\left(\frac{2}{\sqrt{5}}\right)={\cos }^{-1}\left(\frac{1}{\sqrt{5}}\right)\\ & \frac{g}{2v_0^2{\cos }^2{\theta }_0}=9\\ & \Rightarrow \frac{g}{2v_0^2\times \frac{1}{5}}=9\\ & \Rightarrow \frac{10\times 5}{2\times 9}=v_0^2\\ & \Rightarrow v_0^2=\frac{25}{9}\\ & v_0=\frac{5}{3}\mathrm{m}/\mathrm{s}\end{array}$

Hence, the answer is the Option (3).

Example 2: A particle just clears a wall of height b at a distance a and strikes the ground at a distance c from the point of projection. The angle of projection is:

1) ${\tan }^{-1}\left(\frac{bc}{a(c-a)}\right)$
2) ${\tan }^{-1}\left(\frac{bc}{a}\right)$
3) ${\tan }^{-1}\left(\frac{b}{a\ast c}\right)$
4) ${45}^{\circ }$

Solution:

$\begin{array}{rl}& a=(u\cos \alpha )t\text{and}\\ & b=(u\sin \alpha )t-\frac{1}{2}g{t}^2\\ & b=a\tan \alpha -\frac{1}{2}g\frac{a^2}{u^2{\cos }^2\alpha }\\ & \text{also,}c=\frac{u^2\sin 2\alpha }{g}\\ & \Rightarrow b=a\tan \alpha -\frac{a^{2}g}{2}\left(\frac{\sin 2\alpha }{cg}\right){\sec }^2\alpha \\ & \Rightarrow b=a\tan \alpha -\frac{a^2}{2c}2\tan \alpha \\ & \Rightarrow (a-\frac{a^2}{c})\tan \alpha =b\\ & \Rightarrow \tan \alpha =\frac{bc}{a(c-a)}\end{array}$

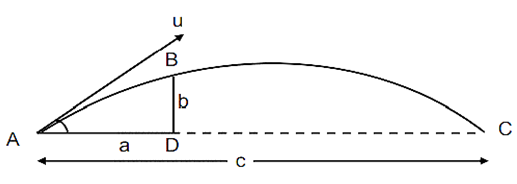
Hence, the answer is option (1).

Example 3: $\text{Position of a particle moving in}x-y\text{plane as a function of time}t\text{is}2t\hat{i}+4t^2\hat{j}\text{. The equation of the trajectory of the particle is :}$

1) $y=x^2$
2) $y=2x$
3) $y^2=x$
4) $y=x$

Solution:

$\begin{array}{rl}& \mathrm{x}=2\mathrm{t}\Rightarrow \mathrm{t}=\mathrm{x}2\\ & \mathrm{y}=4{\mathrm{t}}^2\\ & \text{put}\mathrm{t}=\mathrm{x}/2\text{we get}\mathrm{y}=4{\mathrm{xx}}^2/4\\ & \mathrm{y}={\mathrm{x}}^2\\ & X=2t\\ & Y=4t^2\\ & Y=x^2\end{array}$

Hence, the answer is the option (1).

Example 4: A projectile is given an initial velocity of $(\hat{i}+2\hat{j})\mathrm{m}/\mathrm{s}$, where $\hat{i}$ is along the ground and $\hat{j}$ is along the vertical. If $\mathrm{g}=10\mathrm{m}/{\mathrm{s}}^2$, the equation of its trajectory is :

1) $4y=2x-25x^2$
2) $y=x-5x^2$
3) $y=2x-5x^2$
4) $4y=2x-5x^2$

Solution:

Given :
$\overrightarrow{u}=\hat{i}+2\hat{j}$

From the equation of motion,
$\begin{array}{rl}& \overrightarrow{s}=\overrightarrow{u}t+\frac{1}{2}a{t}^2\\ & \Rightarrow \overrightarrow{r_f}-\overrightarrow{r_i}=(\hat{i}+2\hat{j})t+\frac{1}{2}(-g\hat{j})t^2\\ & \Rightarrow \overrightarrow{r_f}-0=t\hat{i}+2t\hat{j}-\frac{g}{2}{t}^2\hat{j}\\ & \Rightarrow x\hat{i}+y\hat{j}=t\hat{i}+(2t-\frac{g}{2}{t}^2)\hat{j}\end{array}$

After comparing both sides, we get,
$x=t\text{and}y=(2t-5t^2)$

Now, put the value of $\mathrm{t}$ in $y=(2t-5t^2)$

$\text{Note: the above question is solved by the basic method of kinematical equation motion but you can also solve this question by the equation of trajectory of projectile motion. Hint for alternate method :}$
$y=x\tan \theta (1-\frac{x}{R})$
$\mathrm{OR}$,
$y=x\tan \theta -\frac{1}{2}\frac{x^{2}g}{u^2{\cos }^2\theta }$

Hence, the answer is the option (3).

Example 5: A body of mass $10\mathrm{kg}$ is projected at an angle of ${45}^{\circ }$ with the horizontal. The trajectory of the body is observed to pass through a point $(20,10)$. If $\mathrm{T}$ is the time of flight, then its momentum vector, at time $\mathrm{t}=\frac{\mathrm{T}}{\sqrt{2}}$ $$
$[$ Take $g=10\mathrm{m}/{\mathrm{s}}^2]$
$[\text{Take}g=10\mathrm{m}/{\mathrm{s}}^2]$

1) $100\mathrm{i}+(100\sqrt{2}-200)\mathrm{j}$
2) $100\sqrt{2}\hat{\mathrm{i}}+(100-200\sqrt{2})\hat{\mathrm{j}}$
3) $100\hat{\mathrm{i}}+(100-200\sqrt{2})\hat{\mathrm{j}}$
4) $100\sqrt{2}\hat{\mathrm{i}}+(100\sqrt{2}-200)\hat{\mathrm{j}}$

Solution:

$\mathrm{m}=10\mathrm{kg}$

We know that the equation of trajectory is
$\begin{array}{rl}& \mathrm{y}=\mathrm{x}\tan \theta (1-\frac{\mathrm{x}}{\mathrm{R}})\\ & 10=20(\tan {45}^{\circ })(1-\frac{20}{\mathrm{R}})\\ & \frac{1}{2}=1-\frac{20}{\mathrm{R}}\\ & \frac{1}{2}=\frac{20}{\mathrm{R}}\\ & \mathrm{R}=40\to (1)\end{array}$

Also, we know that,

$\begin{array}{rl}& \mathrm{R}=\frac{{\mathrm{u}}^2\sin 2\theta }{\mathrm{g}}\\ & 40=\frac{{\mathrm{u}}^2\sin {90}^{\circ }}{10}\\ & {\mathrm{u}}^2=400\\ & \mathrm{u}=20\mathrm{m}/\mathrm{s}\to (2)\\ & \text{At}\mathrm{t}=\frac{\mathrm{T}}{\sqrt{2}}\\ & \bar{\mathrm{V}}={\bar{\mathrm{v}}}_{\mathrm{x}}+{\bar{\mathrm{V}}}_{\mathrm{y}}\\ & =\mathrm{u}\cos \theta (\hat{\mathrm{i}})+(\mathrm{u}\sin \theta -\mathrm{g})\hat{ȷ}\\ & =10\sqrt{2}\hat{\mathrm{i}}+(10\sqrt{2}-10\times \frac{\mathrm{T}}{\sqrt{2}})\hat{ȷ}\\ & \text{But}\mathrm{T}=\frac{2\mathrm{u}\sin \theta }{\mathrm{g}}=\frac{2\times 20\times }{10}\frac{1}{\sqrt{2}}\end{array}$

$\begin{array}{rl}& \mathrm{T}=2\sqrt{2}\\ & \bar{\mathrm{v}}=10\sqrt{2}\hat{\mathrm{i}}+(10\sqrt{2}-20)\hat{ȷ}\\ & \therefore \text{Momentum vector}=\bar{\mathrm{P}}=\mathrm{m}\bar{\mathrm{v}}\\ & \bar{\mathrm{P}}=100\sqrt{2}\hat{\mathrm{i}}+(100\sqrt{2}-200)\hat{\mathrm{j}}\end{array}$

Hence, the answer is option (1).

Summary

In summary, the equation of the path of a projectile is one of the cornerstone equations of physics, permitting great precision in the prediction and, hence, analysis of such described trajectories of the objects thrown into the atmosphere. This general movement, forming a parabola, due to the known movements under the law of the earth's gravity force in action, is core to understanding and optimizing the trajectory of the moving projectiles in different real-life scenarios.