Uniform Circular Motion - Definition, Examples, Diagram, Characteristic, Examples, FAQs

Uniform circular motion results when an object moves in a circle at a constant speed, which means that the object travels equal distances along the circular path in equal time intervals However, the object has a constantly changing direction.

This article will explore the details of uniform circular motion: just what the differences in forces that permit circular motion are, and how velocity and acceleration work with respect to this kind of motion. This concept falls under the broader category of kinematics which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), a total of nine questions have been asked on this concept. And for NEET five questions were asked from this concept.

This Story also Contains

1. Circular Motion:
2. Circular Motion Examples:
3. Define Uniform Circular Motion :
4. Characteristic of uniform circular motion:
5. Examples of Uniform Circular motion:
6. Angular Acceleration
7. Centripetal Acceleration and Tangential acceleration
8. Solved Example Besed On Uniform Circular Motion
9. Summary

Circular Motion:

Circular Motion Definition: In physics, a body is said to be performing circular motion, if it moves only in a circular path. For example, If a boy is running on a circular track then, motion performed by the boy is said to be circular motion.

Circular Motion Examples:

Some of most common examples of circular motion in our everyday life are listed as:

1. When athletes run in a circular track, the motion performed by athletes is circular motion.
2. Planets revolving around the sun is also an example of circular motion.
3. The blades of the ceiling fan move in circular motion.

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

Circular motion diagram:

When a body moves along a circular path of fixed radius, the circular motion diagram of the body can simply be shown as

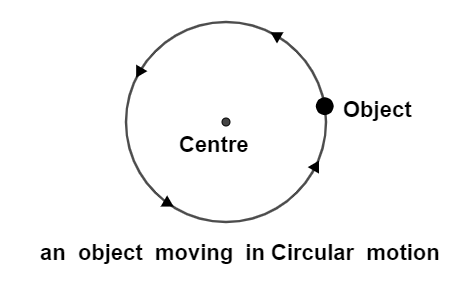
(Source: Self-Drawn using Geogebra)

Related Topic Link - Projectile Motion

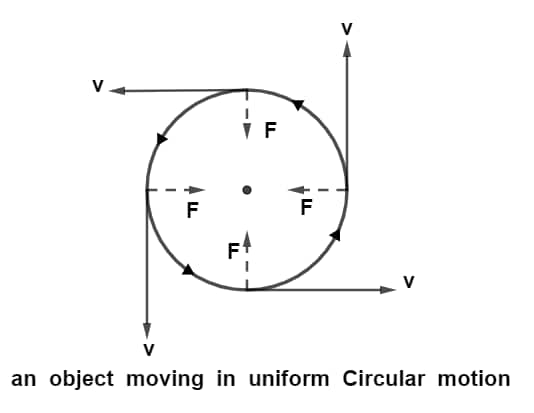
Define Uniform Circular Motion :

Uniform circular motion definition: When a body moves in a circular path but with constant value of speed, the motion governed by the body is said to be uniform circular motion. But velocity of a body in uniform circular motion changes at every instant of the motion.

Uniform circular motion diagram:

Body moving with constant speed in a circular path having uniform circular motion can be shown as:

(Source: Self-Drawn using Geogebra)

Characteristic of uniform circular motion:

Some of important points of uniform circular motion are listed as:

1. The speed of a particle moving in uniform circular motions is always the same.
2. The velocity of a particle performing uniform circular motion is in the direction of tangent at that point and velocity changes at every instant of motion.
3. The force acting on a particle towards the centre of the circular path is called centripetal force.
4. The acceleration of a particle performing uniform circular motion has only a radial component.
5. The tangential component of acceleration of uniform circular motion is always zero.

Acceleration of uniform circular motion:

When a body performs a uniform circular motion, then only the radial acceleration acts on the body which is in the direction towards the centre. If a particle performing uniform circular motion in a circular path having radius of r and speed v then, acceleration acting on the particle is given by a=v2r.

Characteristic of acceleration of uniform circular motion:

Some of important points related to acceleration of a particle performing uniform circular motion are listed as:

1. The direction of acceleration is always towards the centre of the circular path followed by the particle.
2. The acceleration has a constant value as it performs uniform circular motion.
3. Acceleration of uniform circular motion inversely proportional to radius of circular path.
4. Acceleration of uniform circular motion directly proportional to the square of the speed of the particle.
5. Acceleration directed towards the centre of the circular path following uniform circular motion is known as radial acceleration.
6. There is no tangential component of acceleration of a particle performing uniform circular motion.

Force acting on a particle performing Uniform circular motion:

The force which acts on a particle performing uniform circular motion always acts in the direction towards the centre of the circular path and this force is known as Centripetal force.

F=mv2r.

Characteristic of Force in Uniform circular motion:

Some of most common points to be noted of centripetal force are listed as:

1. The Centripetal force has a constant magnitude in uniform circular motion.
2. The direction of centripetal force in uniform circular motion is always towards the centre of the circular path.
3. Centripetal force is directly proportional to acceleration of uniform circular motion and mass of the particle.

Also Read:

• NCERT solutions for Class 11 Physics Chapter 4 Motion in a Plane
• NCERT Exemplar Class 11 Physics Solutions Chapter 4 Motion in a Plane
• NCERT notes Class 11 Physics Chapter 4 Motion in a Plane

Time period of uniform circular motion:

The time taken by a particle performing uniform circular motion in order to cover the total circumference of the circular path is known as the time period of uniform circular motion.

If r, v be the radius of circular path, speed of a particle performing uniform circular motion then, circumference of the circular path is 2πr and if T denoted for time period of uniform circular motion, then T=2πrv.

Characteristic of Time period of uniform circular motion:

Some of important points of time period of a particle performing uniform circular motion are listed as:

1. The value of the time period of uniform circular motion is always constant.
2. Time period of uniform circular motion is directly proportional to the radius of the circular path followed by the particle.
3. Time period of uniform circular motion is inversely proportional to the speed of the particle.

Examples of Uniform Circular motion:

Some of most common examples of a particle performing uniform circular motion are listed as:

1. The motion of blades of a ceiling fan moving with constant speed is an example of uniform circular motion.
2. The motion of atomic particles such as electrons moving around the nucleus in its fixed orbit is also an example of uniform circular motion.
3. The motion of heavenly bodies in the universe rotating about each other due to gravitational force of attraction in fixed orbit is also an example of uniform circular motion.
4. The artificial satellites which when released in their orbit around the earth also perform uniform circular motion.
5. Any object which moves with constant speed and moves in a circular path will be considered as uniform circular motion.

Let's understand this concept better from the solved example given below:

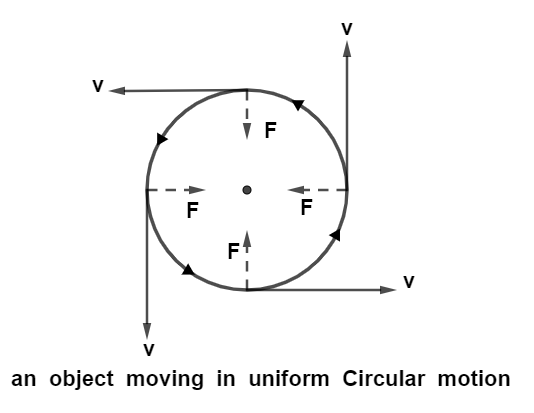
Example :The angular velocity (in radian/sec) of a particle rotating in a circular orbit 100 times per minute is at→=α→×r→at→= tangential acceleration Where r→= radius vector α→= angular acceleration

1) 10.5

2) 10

3) 40.3

4) 20.6

Solution:

Uniform circular motion -

If an object moves in a circular path with a constant speed, then its motion is known as uniform circular motion.

- wherein

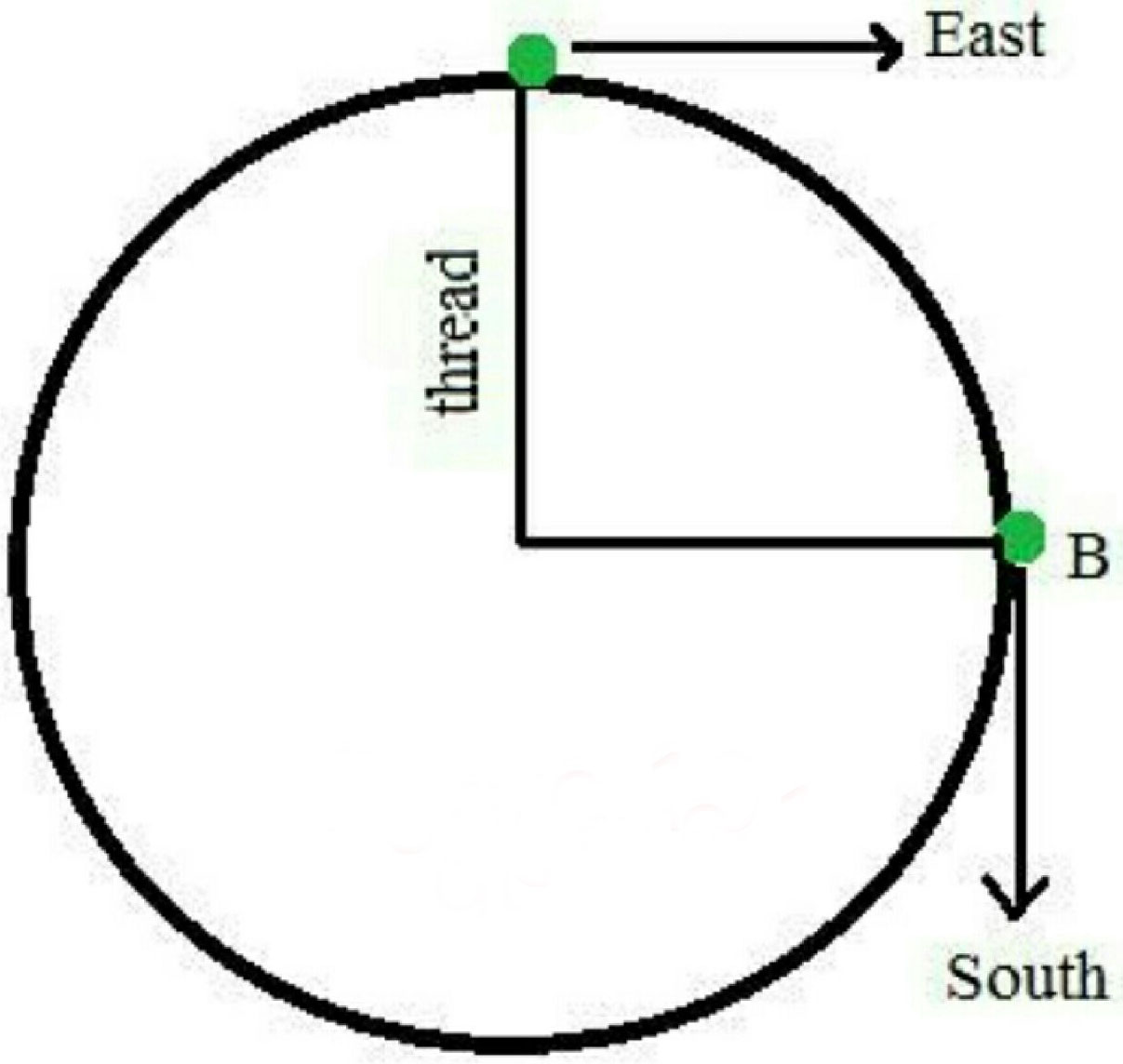
Fig shows Uniform circular of motion

ω= Angle in radian time ω=100×2π(radian)60(sec)=10π3ω=10.47radian/sec

Note: Relation between angular velocity and linear velocity : v→=ω→×r→

Angular Acceleration

The rate of change of angular velocity with time is said to be Angular Acceleration.

α=ΔωΔt

• SI units- rad.(sec)−2
• Angular Acceleration is a vector quantity.

The direction of Angular Acceleration

a) If angular velocity is increasing then the direction of Angular Acceleration is in the direction of angular velocity.

b) If angular velocity is decreasing then the direction of Angular Acceleration is in the direction which is opposite to the direction of angular velocity.

Time is taken to complete one rotation

Formula-

T=2πω

Where ω= angular velocity
If N=no. of revolutions antotalal time then
T=tN or (ω=2πNt)

• S.I unit - seconds (s)

Frequency

The total number of rotations in one second.
Formula-
ν=1T

• S.I. unit = Hertz

We can write the relation between angular frequency and frequency as
w=2πν

Centripetal Acceleration and Tangential acceleration

• Centripetal acceleration: When a body is moving in a uniform circular motion, a force is responsible for changing the direction of its velocity. This force acts towards the centre of the circle and is called centripetal forceThe acceleration produced by this force is centripetal acceleration.

Formula-

ac=V2r

Where ac= Centripetal acceleration,
V= linear velocity
r= radius

Figure Shows Centripetal acceleration

• Tangential acceleration: During circular motion, if the speed is not constant, then along with centripetal acceleration there is also a tangential acceleration, Which is equal to the rate of change of magnitude of linear velocity.

at=dv dt

Relation Between Angular Acceleration and Tangential Acceleration-

at→=α→×r→ Where at→= tangential acceleration r→= radius vector α= angular acceleration

Total acceleration

The vector sum of Centripetal acceleration and tangential acceleration is called Total acceleration.

Formula-

an=ac2+at2

The angle between Net acceleration and tangential acceleration ($\theta$)

From the above diagram-
tan⁡θ=acat

Solved Example Besed On Uniform Circular Motion

Example 1: If a body moving in a circular path maintains a constant speed of 10 ms^-1, then which of the following correctly describes the relation between acceleration and radius?

1)

2)

3)

4)

Solution:

$a=\frac{v^2}{r}$

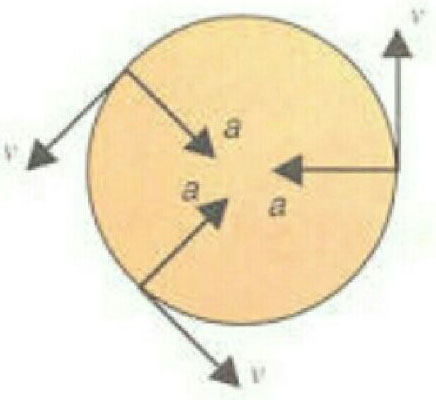
Figure Shows Centripetal acceleration

$\begin{aligned}
& a=\frac{v^2}{r} \because|\vec{v}|=\text { constant } \\
& a \propto \frac{1}{r} \text { or } a r=\text { constant }
\end{aligned}$

Hence, the graph between a and r will be a hyperbola.

Example 2: A Point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of $P$ is such that it sweeps out a length that is in metres and $t$ is in seconds. The radius of the path is $\mathbf{2 0 ~ m}$, The acceleration (in $\mathrm{m} / \mathrm{s}^2$ ) of $P$ When $t=2 s$ is nearly

1) 14

2)13

3)12

4)7.2

Solution:

$
\begin{aligned}
& \text { As } S=t^3+3 \\
& V=\frac{d s}{d t}=3 t^2+0 \\
& \Rightarrow v=3 t^2
\end{aligned}
$
tangential acceleration
$
\begin{aligned}
& =a_t=\frac{d v}{d t}=\frac{d\left(3 t^2\right)}{d t} \\
& a_t=6 t
\end{aligned}
$

At $t=2 \mathrm{sec}$
$
\begin{aligned}
& v=3(2)^2=12 \mathrm{~ms}^{-1} \\
& a_t=6 \times 2=12 \mathrm{~ms}^{-2}
\end{aligned}
$
$
\begin{aligned}
& \therefore \text { centripetal acceleration }=\vec{a}_c=\frac{v^2}{r}=\frac{(12)^2}{20}=\frac{144}{20} \\
& a_c=7.2 \mathrm{~ms}^{-2}
\end{aligned}
$

$\therefore$ Net acceleration
$
\begin{aligned}
& a=\sqrt{a_c^2+a_t^2}=\sqrt{7.2^2+12^2} \\
& a_c \simeq 14 \mathrm{~ms}^{-2}
\end{aligned}
$

Example 3: A particle is moving with speed varying as v = 2t, then the angle which resultant acceleration makes with radial direction (R=1m) at t = 2 is

1)$\tan^{-1}\left(\frac{1}{2} \right )$

2)$\tan^{-1}\left(\frac{1}{6} \right )$

3)$\tan^{-1}\left(\frac{1}{8} \right )$

4)$\tan^{-1}\left(\frac{1}{4} \right )$

Solution:

The angle between Total acceleration and centripetal acceleration is given by
$
\tan \phi=\frac{a_t}{a_c}=\frac{r^2 \alpha}{V^2}
$
where
$\alpha=$ angular acceleration
$V=$ velocity
$r=$ radius of circle
So From the below figure

$\begin{aligned}
& \tan \theta=\frac{a_t}{a_r} \\
& a_t=\frac{\mathrm{d} v}{\mathrm{~d} t}=2 \mathrm{~m} / \mathrm{s}^2 \\
& a_r=\frac{v^2}{R} \\
& a_r=\frac{4 t^2}{1}=4 \times 2^2=16 \\
& \therefore \tan \theta=\frac{2}{16}=\frac{1}{8} \\
& \therefore \theta=\tan ^{-1}\left(\frac{1}{8}\right)
\end{aligned}$

Example 4:A particle is moving with a constant speed of 8 m/s in a circular path of radius 1 m. What will be the displacement of the particle in 1 sec?

1) 2 sin 8⁰

2) 2 sin 4⁰

3) 4 sin 8⁰

4) 4 sin 4⁰

Solution:

Displacement in Circular Motion -

$
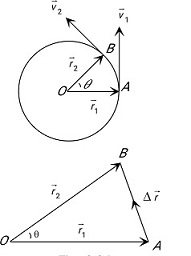
\Delta r=2 r \sin \frac{\theta}{2}
$
$\Delta r=$ displacement
$\theta=$ Angle between two vectors
- wherein
$
\text { If }\left|\overrightarrow{r_1}\right|=\left|\overrightarrow{r_2}\right|=r
$

Let the angular displacement of the particle from $\mathrm{A}$ to $\mathrm{B}$ will be
$
2 R \sin \frac{\Theta}{2}
$

Length of circular arc $A B=8 * 1=8 \mathrm{~m}$
$
\begin{aligned}
& \text { Angle } \Theta=\frac{\text { arc length }}{\text { Radius }}=\frac{\Theta}{1}=8 \mathrm{rad} \\
& d=2 R \sin \frac{\Theta}{2}=2 * 1 * \sin \frac{8}{2} \\
& 2 \sin 4^0
\end{aligned}
$

Hence, the correct answer is option (2).

Summary

Circular motion involves a particle moving along a circular path at a constant speed, with its velocity continuously changing due to the changing direction. A common example is a merry-go-round, where objects move in circles at a uniform speed. This concept also applies to natural phenomena like planets orbiting the sun. Understanding uniform circular motion helps us grasp how forces and motion work in circular paths, essential for both everyday experiences and comprehending larger cosmic movements.