Fermi Energy - Definition, Formula, FAQs
Fermi energy is a concept in quantum physics that usually pertains to the energy difference between the very best and lowest occupied single-particle states during a quantum system of non-interacting fermions at temperature. In this article, we will discuss what is Fermi level, what is Fermi energy, what is Fermi level in semiconductors, what is Fermi energy level, the Fermi energy formula, the application of Fermi energy and values of Fermi energy in different materials.
JEE Main/NEET 2027: Physics Important Formulas for Class 10
NEET 2025: Mock Test Series | Syllabus | High Scoring Topics | PYQs
JEE Main: Study Materials | High Scoring Topics | Preparation Guide
JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs
What is Fermi?
A unit of length adequate to $10^{-15}$ metres (one femtometre), is utilized in atomic (nuclear) physics. It’s almost like the diameter of a proton. The meaning of Fermi is “Above”.
The Fermi is a unit that measures length. The Fermi function determines the probability that an energy level ($E$) is crammed with an electron when the fabric we are working with is under equilibrium conditions.
What is Fermi Level (Electrochemical potential)?
Fermi level definition: At absolute zero temperature, the highest level occupied by an electron is called the Fermi level. When the transfer is complete, the Fermi levels of the 2 materials are equal.
What is Fermi Energy?
Fermi energy definition: Named after the Physicist by name Fermi. At absolute zero temperature, the energy occupied by an electron is called the Fermi energy. It is often defined as:
Fermi energy is a concept in quantum mechanics usually about the energy of the greatest occupied quantum state during a system of fermions at absolute 0 temperatures.
Fermi Energy Formula
The equation for Fermi energy is given by:
$$
E_{\mathrm{F}}=\frac{\hbar^2}{2 m_0}\left(\frac{3 \pi^2 N}{V}\right)^{2 / 3}
$$
Where,
- $N$= number of particles
- $m_0$= rest mass of each fermion
- $V$ = volume of the system
- $ h$ = reduced Planck constant
Using this definition of Fermi energy, various related quantities can be useful.
The Fermi temperature is defined as
$T_F=\frac{E_F }{ k_B}$
Where,
$\mathrm{k}_{\mathrm{B}}$ = Boltzmann constant
$E_F$ = Fermi energy
The Fermi temperature is often thought of because of the temperatures at which thermal effects are like quantum effects related to Fermi statistics. The Fermi temperature for metal may be a few orders of magnitude above temperature.
Other quantities defined in this context are Fermi momentum.
$p_F=\sqrt{2 m_0 E_F}$
And Fermi velocity:
$\mathrm{v}_{\mathrm{F}}=\frac{\mathrm{p}_{\mathrm{F}} }{ \mathrm{m}_0}$
These quantities sequentially represent the momentum and group velocity of a fermion at the Fermi surface.
The Fermi momentum can also be represented as
$p_{\mathrm{F}}=\hbar k_{\mathrm{F}}$
Where
$k_F$ = Fermi wave vector is the radius of the Fermi sphere
Calculating Fermi Energy
The lowest possible Fermi energy of a system is calculated by grouping the states with equal energy into sets and order according to the increasing energy level. On successive addition of particles with time and filling up the unoccupied quantum states with the lowest energy.
When all the particles are arranged accordingly, the energy of the highest occupied state is the Fermi energy. Despite the extraction of all possible energy from metal by cooling it to near absolute zero temperature ($0$ Kelvin), the electrons in the metal still move around. The fastest ones move at a velocity corresponding to a kinetic energy equal to the Fermi energy.
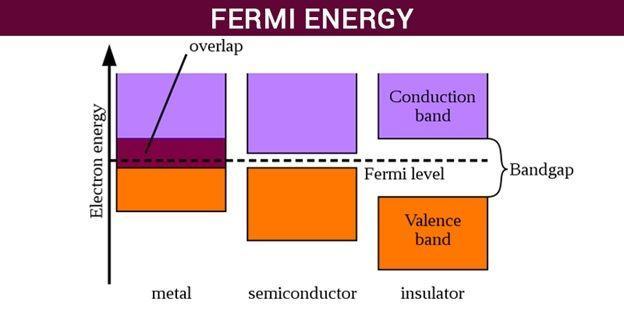
The Fermi level and Fermi energy are usually confusing terms and are sometimes used interchangeably to refer to one another. Although both the terms are equal at one temperature, they're different at other temperatures.
Fermi energy is applied to finding the electrical and thermal characteristics of the solids. It’s one of the important concepts in superconductor physics and quantum physics. It’s utilized in semiconductors and insulators.
|
Related Topics, |
What is Fermi Energy Level?
The probability of occupation of energy levels in the valence band and conduction band is named Fermi level.
In intrinsic or pure semiconductors, the amount of holes in the valence band is adequate for the amount of electrons within the conduction band. Hence, the probability of occupation of energy levels in the conduction band and valence band are the same. Hence, the Fermi level for the intrinsic semiconductor lies under the middle of the forbidden band.
Metals
Under the electron model, the electrons in a metal are often considered to make a Fermi gas. The number density $N/V$ of conduction electrons in metals ranges between $10^{28}$ and $10^{29}$ electrons $/ \mathrm{m}^3$ . It is responsible for the Fermi energy of the order of 2 to 10 electron volts.
What is Fermi Level in Semiconductor
At absolute zero temperature, the highest energy level occupied by an electron in the conduction band is called the Fermi energy.
Electrons settle into rock bottom available energy states at temperature and build a "Fermi sea" of electron energy states. The Fermi Level (with Fermi energy $E_f$) is the “surface” of this ocean where electrons won't have enough energy to rise above the surface. It’s the energy state that is settled by the very best electron orbital at $0$ Kelvin (absolute 0 temperature) and a parameter of the Fermi-Dirac distribution:
$$
f(E)=\frac{1}{1+e^{\left(E-E_f\right) / k T}}
$$
Where,
- T= absolute temperature
- k = Boltzmann’s constant
The above function represents the probability f (E) of an electron to occupy a state with energy E. For electrical conduction to take place, the distribution function has to be non-zero in the conduction band. In solids, the probability of occupancy with the energy level decides whether a material is a conductor, semiconductor, or insulator.
There’s a function between the valence and transfer (conduction) band called the energy gap; the higher the energy gap, the more energy is needed to transfer the electron from the valence band to the conduction band. At the Fermi level (when $\mathrm{E}=\mathrm{E}_{\mathrm{f}}$), the probability simplifies to ½, and thus $E_f$ lies halfway between the valence and conduction band, or within the middle of the energy gap ($E_{\text {gap }} / 2$).
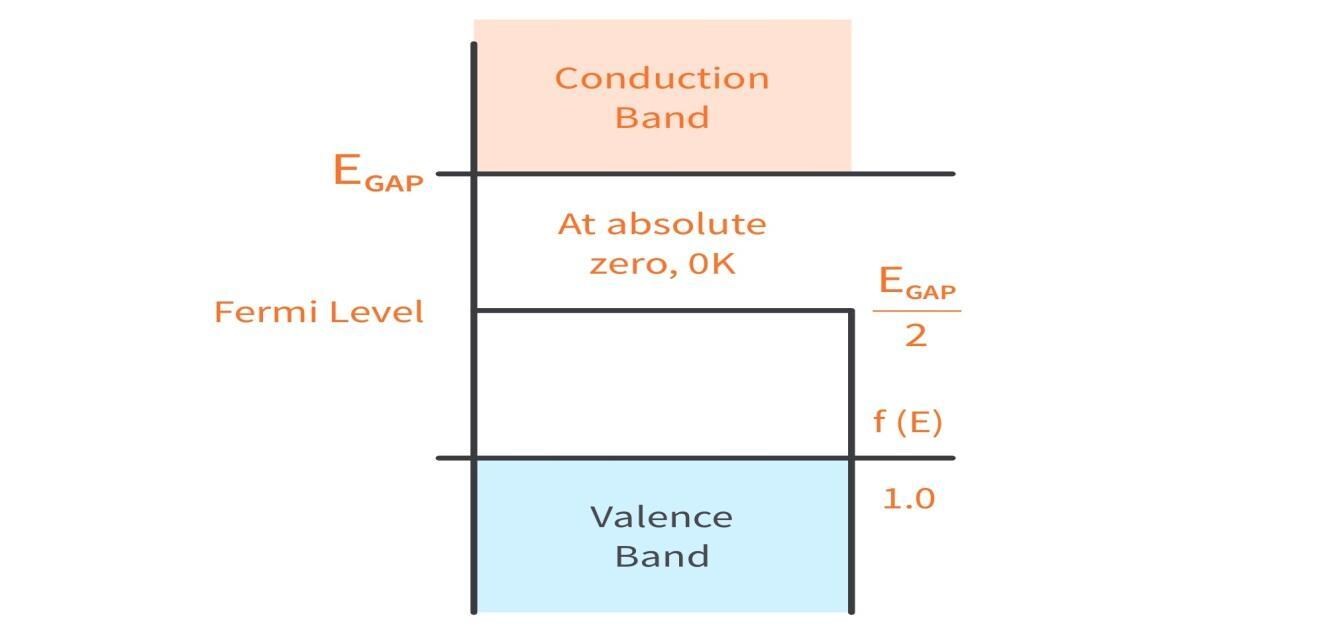
For semiconductors, electrons occupying the transfer (conduction) band level mean the capability of conducting electricity with energy. At higher temperatures, more electrons can bridge the energy gap and contribute to conduction.
The Fermi level is usually positioned somewhere under the band gap for any semiconductor material when it is intrinsic. The doped/ Fermi level for extrinsic semiconductors depends on the doping concentration and the kind of dopant used (p or n-type).
For conduction to occur, the Fermi level lies above the valence band since the density of states (DOS) is greater there. For p-type semiconductors, since the free obtainable electrons are delocalized in the products, the Fermi level might drop down to the valence band since the DOS accordingly decreases. Just the opposite occurs in the case of n-type semiconductors; because of maximum free electrons, DOS around the transfer (conduction) band goes up, and the Fermi level increases. The position of Fermi level in intrinsic semiconductors lies in the middle of the forbidden gap.
Fermi Energy Values For Different Materials
| Material | Fermi Energy (EF) (eV) |
| Copper (Cu) | 7 |
| Gold (Au) | 5.5 |
| Silver (Ag) | 5.5 |
| Aluminum (Al) | 11.7 |
| Iron (Fe) | 11.1 |
| Lead (Pb) | 9.5 |
| Silicon (Si) | 1.1 |
| Germanium (Ge) | 0.67 |
| Graphene | 0.3-0.5 |
| Sodium (Na) | 3.2 |
| Potassium (K) | 2.1 |
| Tungsten (W) | 8.1 |
| Platinum (Pt) | 5.7 |
| Zinc (Zn) | 9.5 |
Applications Of Fermi Energy
- It is used in metals to find the density of free electrons resulting in electrical conductivity.
- Helps in understanding electronic devices like diodes and transistors
- It is used to differentiate conductors, semiconductors, and insulators with the help of Fermi energy levels.
- It helps to describe the behavior of electron gases in cryogenic systems.
- Helps in describing the electron degeneracy pressure in stars.
Also, check
Frequently Asked Questions (FAQs)
Quasi-Fermi energy level is defined as the converter in the level of Fermi level as the charge porter are added inordinately to the semiconductor.
It is one among the important concepts in quantum physics and condensed matter physics. Some Fermi energy applications are given within the points below.
It is utilized in semiconductors and insulators.
It is wont to describe insulators, metals, and semiconductors.
Fermi energy is applied in finding the electrical and thermal characteristics of the solids.
It is also important in atomic physics to know the steadiness of white dwarfs. White dwarfs are stars that have a mass like the Sun but have a few hundredth of its radius
Angle, Poisson’s ratio, strain, specific gravity.
Also Read
28 Nov'24 01:14 AM
16 Nov'24 01:37 PM
14 Nov'24 05:50 PM
12 Nov'24 01:15 AM
24 Sep'24 04:35 PM