Force On A Moving Charge In Magnetic Field

A force on a moving charge in a magnetic field is a fundamental concept in physics, particularly in the study of electromagnetism. When a charged particle, such as an electron or proton, moves through a magnetic field, it experiences a force perpendicular to both its velocity and the magnetic field. This phenomenon is described by the Lorentz force law, which is crucial for understanding the behaviour of charged particles in various applications. In real life, this principle is at work in numerous technologies. For instance, it's the driving force behind electric motors, where current-carrying conductors in a magnetic field create motion. It's also essential in the operation of particle accelerators used in medical and scientific research, as well as in the natural world, where it explains the behaviour of cosmic rays and the auroras near the Earth's poles. In this article, we will discuss the concept of force on a moving charge in a magnetic field, the right-hand rule and solved examples for better clarity.

This Story also Contains

1. Force on a Moving Charge in a Magnetic Field
2. Solved Examples Based on Force on a Moving Charge in Magnetic Field
3. Summary

Force on a Moving Charge in a Magnetic Field

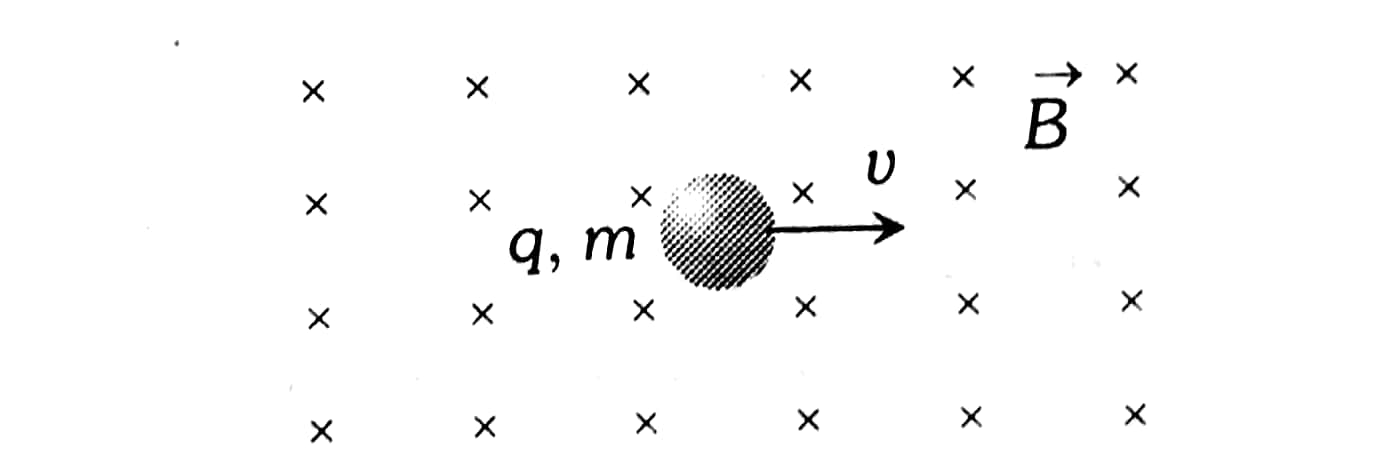
The magnetic force on a free-moving charge is perpendicular to both the velocity of the charge and the magnetic field with direction given by the right-hand rule. The force is given by the charge times the vector product of velocity and magnetic field.

The force is always perpendicular to both the magnetic field and velocity.

$\begin{array}{rl}& F=qvB\sin \theta \\ & F=qvB\text{if}\theta =90\end{array}$

If the velocity is perpendicular to the magnetic field then the force is given by the simple product :

Force = charge x velocity x B-field

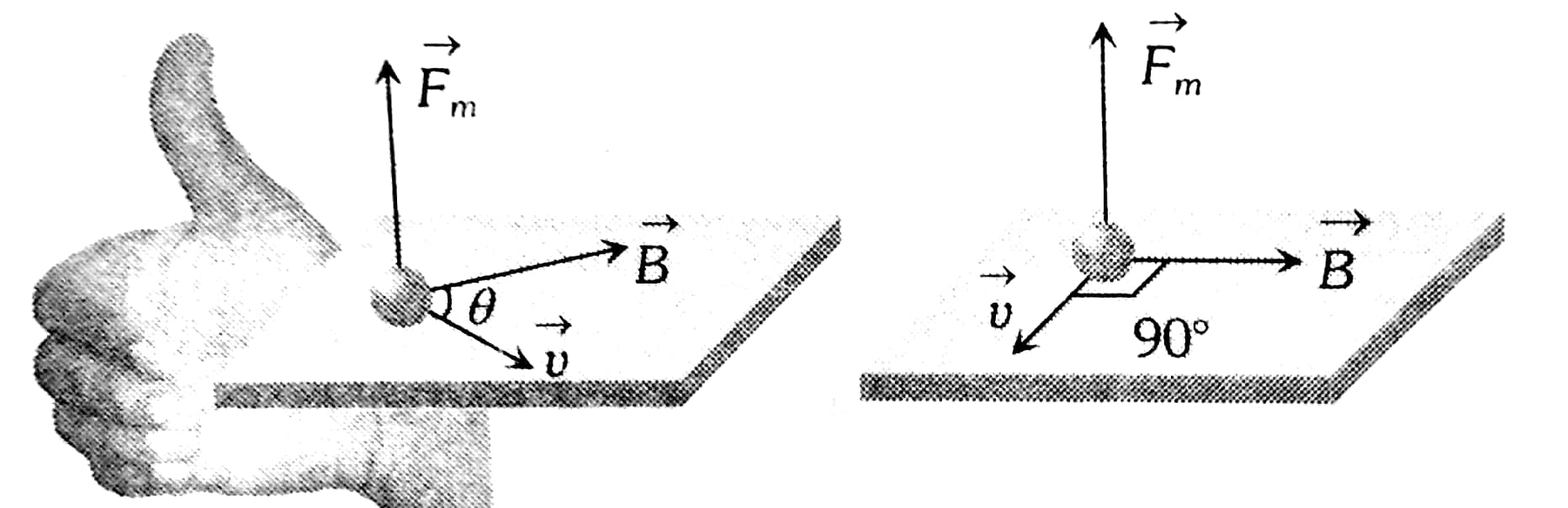
Right-Hand Rule

Magnetic force is as important as the electrostatic or Coulomb force. Yet the magnetic force is more complex, in both the number of factors that affects it and in its direction, than the relatively simple Coulomb force. The magnitude of the magnetic force F on a charge q moving at a speed v in a magnetic field of strength B is given by

$F=qvB\sin \theta$,

where θ is the angle between the directions of v and B. This force is often called the Lorentz force. In fact, this is how we define the magnetic field strength B—in terms of the force on a charged particle moving in a magnetic field. The SI unit for magnetic field strength B is called the tesla (T). Therefore magnetic field strength is given as

$B=\frac{F}{qv\sin \theta }$

The unit of Tesla is :

$1\mathrm{T}=\frac{1\mathrm{N}}{\mathrm{C}\cdot \mathrm{m}/\mathrm{s}}=\frac{1\mathrm{N}}{\mathrm{A}\cdot \mathrm{m}}$

The direction of the force on a moving charge is given by the right-hand rule. Point the thumb of the right hand in the direction of v, the fingers in the direction of B, and a perpendicular to the palm points in the direction of F.

The force is perpendicular to the plane formed by v and B. Since the force is zero if v is parallel to B, charged particles often follow magnetic field lines rather than cross them.

Recommended Topic Video

Solved Examples Based on Force on a Moving Charge in Magnetic Field

Example 1: A particle mass m and charge q is in an electric and magnetic field is given by $\overrightarrow{E}=2\hat{i}+3\hat{j};\overrightarrow{B}=4\hat{j}+6\hat{k}$. The charged particle is shifted from the origin to the point P(x = 1, y = 1)along a straight path. The magnitude of the total work done is:

1)(0.15)q

2)(0.35)q

3) 5q

4)(2.5)q

Solution:

Force on a charged particle in a magnetic field

$\begin{array}{rl}& \overrightarrow{F}=q(\overrightarrow{V}\times \overrightarrow{B})\\ & F=qVB\sin \theta \end{array}$

wherein

$\begin{array}{rl}& \overrightarrow{V}\text{- velocity of the particle}\\ & \overrightarrow{B}\text{magnetic field}\\ & E=2\hat{i}+3\hat{j}\\ & \overrightarrow{B}=4\hat{j}++6\hat{k}\\ & 0(0,0)\\ & OP=S=1\hat{i}+1\hat{j}\\ & W=F_{\text{net}}\cdot S\\ & \overrightarrow{F_{net}}=q\overrightarrow{E}+q(\overrightarrow{V}\times \overrightarrow{B})\end{array}$

$\overrightarrow{V}\times \overrightarrow{B}$ is perpendicular to $\overrightarrow{V}$
So $\overrightarrow{V}\times \overrightarrow{B}$ is perpendicular to $\overrightarrow{S}$
So $W_B=q(\overrightarrow{V}\times \overrightarrow{B})\cdot \overrightarrow{S}=0$
$\begin{array}{rl}{W}_E& =(q\overrightarrow{E})\cdot \overrightarrow{S}\\ & =q(2\hat{i}+3\hat{j})(1\hat{i}+1\hat{j})\\ & =5q\end{array}$
in an electric and magnetic field is given
$W_{net}=W_E+W_B=5q$

Hence, the answer is the option (3).

Example 2: A solid metal cube of edge length 2 cm is moving in a positive y-direction at a constant speed of 6m/s. There is a uniform magnetic field of 0.1 T in the positive z-direction. The potential difference (in mV) between the two faces of the cube perpendicular to the x-axis, is:

1) 12

2)6

3)1

4)2

Solution:

Given
$l=2\mathrm{cm}$
${\epsilon }_x=\mathrm{Emf}=$ P.D. between two faces of cubes perpendicular to $x-$ axis
$\begin{array}{r}\text{so}{\epsilon }_x=l(V\times B)\\ =\frac{2}{{10}^2}((6\times 0.1))\\ V=6\mathrm{m}/\mathrm{s}{\epsilon }_x=12\mathrm{mV}\end{array}$

Hence, the answer is the option (1).

Example 3: A very high magnetic field is applied to a stationary charge then the charge experiences

1)Force in the direction of $\overrightarrow{B}$

2)Force in an arbitrary direction

3)No force

4)Force $\perp$ to B

Solution:

The force experienced by a charged particle in the magnetic field is given by: $F=qVB\sin \theta$

For a stationary charge, velocity will be zero.

$F=qVB\sin \theta$

If V=0,

F=0

So, the force experienced by a stationary charge particle will be zero.

Hence, the answer is the option (3).

Example 4: A particle of mass M and charge Q moving with velocity $\overrightarrow{v}$ describes a circular path of radius R when subjected to a uniform transverse magnetic field of induction B. The work done by the field when the particle completes one full circle is

1) $\left(\frac{M{v}^2}{R}\right)2\pi R$
2) zero
3) $BQ2\pi R$
4) $BQv2\pi R$

Solution:

Direction of Force (Right-hand screw rule)

The force $\overrightarrow{F}$ is always perpendicular to both $\overrightarrow{V}$ and may or may not be perpendicular to each other

wherein

Force is always perpendicular to displacement hence Work done by the magnetic field = zero.

Hence, the answer is the option (2).

Example 5: Two ions having the same mass have charges in the ratio $1:2$. They are projected normally in a uniform magnetic field with their speeds in the ratio $2:3$. The ratio of the radii of their circular trajectories is :

1) $1:4$
2) $4:3$
3) $3:1$
4) $2:3$

Solution:

$\begin{array}{rl}& F=qvB\sin {90}^{\circ }=\frac{m{v}^2}{r}\\ & rqB=mv\\ & \frac{r_1}{r_2}=\frac{m_1{v}_1}{m_2{v}_2}\times \frac{q_2{B}_2}{q_1{B}_1}\\ & \frac{q_1}{q_2}=\frac{1}{2}\\ & m_1=m_2\\ & \frac{v_1}{v_2}=\frac{2}{3}\\ & \frac{r_1}{r_2}=\frac{2}{3}\times \frac{2}{1}\times 1=\frac{4}{3}\end{array}$

Summary

The force on a moving charge in a magnetic field, governed by the Lorentz force law, plays a crucial role in understanding electromagnetic phenomena. It is responsible for the operation of electric motors, particle accelerators, and even natural occurrences like the auroras. This article explores the concept, its mathematical formulation, and the right-hand rule for determining the force's direction, and includes solved examples to illustrate its practical applications.