Lens Formula - Calculating Magnification Formula, FAQs

The lens magnification formula is a fundamental concept in optics, playing a crucial role in understanding how lenses affect the appearance of objects. Magnification, defined as the ratio of the image size to the object size, helps us determine how much larger or smaller an object appears when viewed through a lens. This article will explore what is lens formula, magnification, derivation of lens magnification formula, its application in real-world scenarios, and its significance in both scientific and daily contexts.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. What is Lens Formula?
2. Define Magnification And Magnification Formula
3. Magnification
4. Magnification Of Convex Lens
5. Magnification of Concave Lens
6. Practical Applications Of Magnification Of Lens
7. Power Of Lens Formula
8. Summary

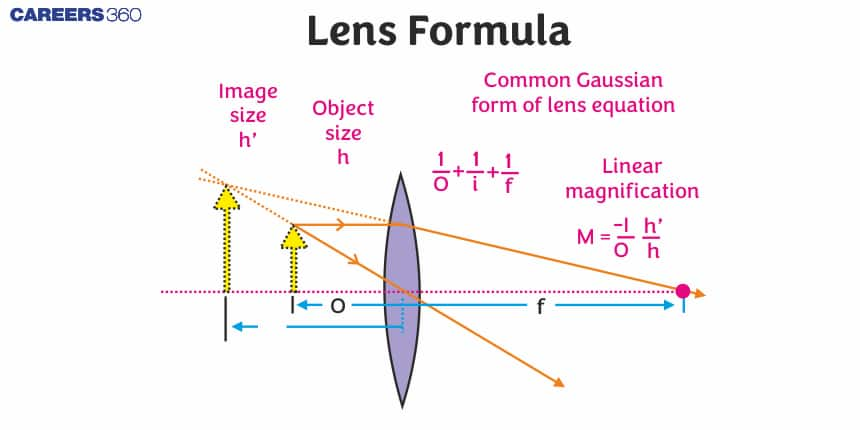
What is Lens Formula?

In optical physics, spherical lenses are lenses made by combining two spherical surfaces. These lenses are divided into two categories based on the notion of formation by binding two surfaces: convex lenses, which are created by binding two spherical surfaces curved outward, and concave lenses, which are formed by binding two spherical surfaces curved inward.

Depending on the distance between the lens and the objects, the images created by these lenses can be actual, virtual, or of varied sizes. The formula of lens now assists us in determining the picture distance. It is the formula, or the equation, that links the focal length formula, object distance, and image distance for a lens.

The Lens formula describes the relationship between the distance of an image (v), the distance of an object (u), and the focal length of the lens formula (f) of the lens in optics. The lens formula works for both convex and concave lenses. The thickness of these lenses is minimal. The following is the formula of lens:

$$\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$$

Where,

• $v$ is the Image formation distance from the lens's optical center.
• $u$ is the object's distance from the lens's optical center.
• $f$ is the focal length formula of the lens.

The lens formula applies to both convex and concave lenses. It can also be used to figure out how far real and virtual images are apart. If the equation yields a negative image distance, the resulting picture is virtual and on the same side as the item. The lens is diverging rather than converging if the equation returns a negative focal length formula.

Also read -

• NCERT Solutions for Class 11 Physics
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for All Subjects

Define Magnification And Magnification Formula

Converging and diverging lenses are optical physics miracles that employ these media's ability to refract, reflect, or bend light beams. In general, there are two types of lenses: convex (curved outward) and concave (curved inward) (curved inward). One of its primary functions is to magnify images, making them look larger than they are. These lenses can now be found in microscopes, telescopes, binoculars, and other optical devices, as well as our own eyes. Scientists and students can use a variety of simple to complicated algebraic equations to link a lens' shape and physical characteristics to the impact it has on light rays passing through it.

Magnification

Magnification is a measure of how much larger or smaller an image appears compared to the actual object.

Magnification Formula For Lens

The magnification of a lens is the ratio of the height of the image to the height of the object.

OR

It is the ratio of image distance to that of object distance.

$$\begin{aligned} & m=\frac{\text { Height of the image }}{\text { Height of the object }} \\ & m=\frac{h_i}{h_o}\end{aligned}$$

where,

• $m$ is the magnification
• $h_i$ is the height of the image
• $h_o$ is the height of the object

OR

$$\begin{aligned} m & =\frac{\text { Image Distance }}{\text { Object Distance }} \\ m & =\frac{v}{u}\end{aligned}$$

where,

• $m$ stands for magnification.
• $v$ is image distance.
• $u$ is the object distance

Magnification Of Convex Lens

Magnification produced by the convex lens be either positive or negative depending on the image characteristics.

(i) Object beyond 2F

• Image is real, inverted, smaller than the object
• Magnification: $|m|<1$

(ii) Object at 2F

• Image is real, inverted, same size as the object
• Magnification: $|m|=1$

(iii) Object between F and 2F

• Image is real, inverted, larger than the object.
• Magnification : $|m|>1$

(iv) Object within F

• Image is virtual, upright, larger than the object.
• Magnification:$|m|>1$

Magnification of Concave Lens

• Magnification of a concave lens is always positive as the image formed is virtual.
• The image distance is negative for virtual images
• The object distance is negative according to sign convention.
• The magnification is always positive : $|m|>0$
• The value of magnification is less than one: $|m|<1$

Also Read:

• NCERT solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
• NCERT Exemplar Class 12 Physics Solutions Chapter 9 Ray Optics and Optical Instruments
• NCERT notes Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

Practical Applications Of Magnification Of Lens

• Microscopes: Use high magnification to observe small specimens
• Telescopes: Magnify distant celestial objects in the sky.
• Cameras: Adjust lens settings to get the desired image

Power Of Lens Formula

• The ability of a lens to focus light rays falling on it is its power. In other words, it's a measurement of how close the rays of light falling on the lens are converged or diverged.
• The power of a lens can be described as the reciprocal of the focal length of the lens because the degree of convergence or divergence of the rays is determined by the focal length of the lens.

$$P=\frac{1}{\text { Focal Length }}$$

$$P=\frac{1}{f}$$

• The dioptre is the SI unit of lens power and is sometimes abbreviated as D. 1 dioptre is the power of a lens with a focal length of 1 meter.
• For a concave lens' focal length is negative, its power is negative (-), whereas the power of a convex lens is positive (+) because its focal length is positive.

Also check-

• NCERT Exemplar Class 11th Physics Solutions
• NCERT Exemplar Class 12th Physics Solutions
• NCERT Exemplar Solutions for All Subjects

Summary

The magnification of lenses is integral to various applications to improve our ability to analyze objects. From everyday needfuls like eyeglasses to advanced scientific instruments, lenses play a vital role in expanding our vision. In this article, we discussed the lens formula, magnification of the concave lens, magnification of the convex lens, Power of the lens, and everyday and scientific applications of magnification of the lens.

NCERT Physics Notes:

• NCERT Notes Class 11th Physics
• NCERT Notes Class 12th Physics
• NCERT Notes For All Subjects