Moving Coil Galvanometer

A moving coil galvanometer is an essential instrument in the field of physics, designed to measure small electric currents with high precision. It operates on the principle that a current-carrying coil, placed within a magnetic field, experiences a torque proportional to the current. This device is a cornerstone in electrical measurements, transforming minute currents into observable mechanical deflections. In real life, the moving coil galvanometer finds its applications in various fields, including electronics and instrumentation. For instance, in a household analogue multimeter, the galvanometer serves as a core component, enabling users to measure current, voltage, and resistance accurately. Furthermore, it plays a crucial role in scientific research and education, helping students and professionals understand and analyze the behaviour of electric circuits. The device's sensitivity and reliability make it indispensable in developing and testing new electronic devices, ensuring their proper functionality and safety. In this article, we will discuss the Moving Coil Galvanometer and provide examples for better understanding.

JEE Main/NEET 2027: Physics Important Formulas for Class 10

NEET 2025:  Mock Test Series | Syllabus | High Scoring Topics | PYQs

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

1. What is a Moving Coil Galvanometer?
2. Solved Examples Based on Moving coil Galvanometer
3. Example 1: An ammeter reads up to 1 ampere. Its internal resistance is 0.81 ohm. To increase the range to 10 A, the value of the required shunt is (in $\mathrm{\Omega }$)
4. Summary

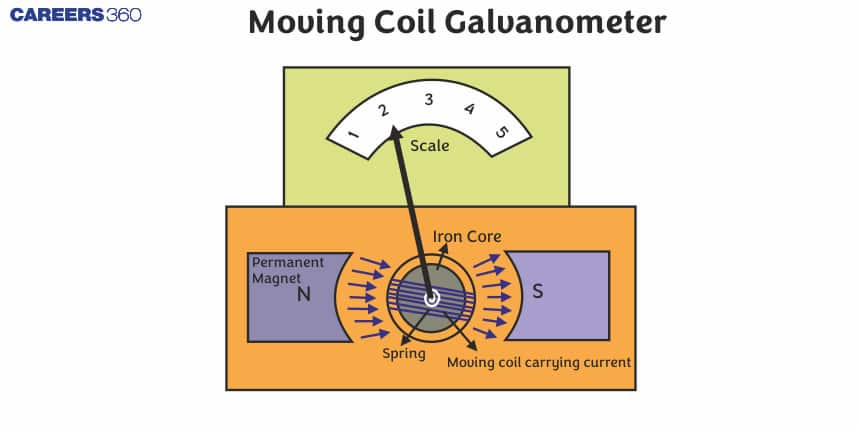
What is a Moving Coil Galvanometer?

A moving coil galvanometer is an electromagnetic device which is used to measure small values of current. It consists of a permanent horse-shoe magnet, coil, soft iron core, pivoted spring, non-metallic frame, scale, and pointer as shown in the figure.

As we have studied the torque acts on a current-carrying coil suspended in the uniform magnetic field. Due to this, the coil rotates. Hence, the deflection in the coil of a moving coil galvanometer is directly proportional to the current flowing in the coil.

In this, the coil is suspended between the pole pieces of a strong horse-shoe magnet. The magnetic field is made radial and for this, the pole pieces are made cylindrical and a soft iron cylindrical core is placed within the coil without touching it. The benefit of this type of field is that the plane of the coil always remains parallel to the field. Therefore θ=90^o and the deflecting torque always has the maximum value.

${\tau }_{\text{deflection }}=NBiA$

Now if the coil deflects, a restoring torque is set up in the pivoted spring. If $\alpha$ is the angle of twist, the restoring torque is

${\tau }_{\text{restoring }}=C\alpha$

where C is the torsional constant of the fibre.

When the coil is in equilibrium, then

$NBiA=C\alpha \text{, }$

So, $i=\frac{C}{NBA}\cdot \alpha \Rightarrow i=K\alpha$
where $K=\frac{C}{NBA}$ is the galvanometer constant.

This linear relationship between i and $\alpha$ makes the moving coil galvanometer useful for current measurement and detection.

Here we will discuss two important terminologies

1. Current sensitivity (S_i): The current sensitivity of a galvanometer is defined as the deflection produced in the galvanometer per unit of current flowing through it. So it can be written as

$S_i=\frac{\alpha }{i}=\frac{NBA}{C}$

2. Voltage sensitivity (S_V): The voltage sensitivity of a galvanometer is defined as the deflection produced in the galvanometer per unit voltage applied to it. So it can be written as -

$S_V=\frac{\alpha }{V}=\frac{\alpha }{iR}=\frac{S_i}{R}=\frac{NBA}{RC}$
(By using Ohm's law)

Recommended Topic Video

Solved Examples Based on Moving coil Galvanometer

Example 1: An ammeter reads up to 1 ampere. Its internal resistance is 0.81 ohm. To increase the range to 10 A, the value of the required shunt is (in $\mathrm{\Omega }$)

1) 0.09

2) 0.3

3) 0.9

4) 0.03

Solution:

Moving coil galvanometer

It is a very sensitive instrument used to measure the small current. The galvanometer gives the deflection which is proportional to the electric current flowing through it.

$\begin{array}{rl}& \frac{S}{S+G}=\frac{I_g}{I}\Rightarrow S=\frac{I_{g}G}{I-I_g}\\ & \therefore S=\frac{1\times 0.81}{10-1}=\frac{0.81}{9}=0.09\mathrm{\Omega }\text{ in parallel. }\end{array}$

Hence, the answer is the option (1).

Example 2: A moving coil galvanometer has 150 equal divisions. Its current sensitivity is 10 divisions per milliampere and voltage sensitivity is 2 divisions per millivolt, so that each division reads 1 volt, the resistance in ohms needed to be connected in series with the coil will be

1) 9995

2) 99995

3) 10³

4) 10⁵

Solution:

Moving coil galvanometer

It is a very sensitive instrument used to measure the small current. The galvanometer gives the deflection which is proportional to the electric current flowing through it.

$\begin{array}{rl}& V_{max}=\frac{150}{2}=75\mathrm{mV}\\ & I_{max}=\frac{150}{10}=15\mathrm{mA}=I_g\end{array}$

Resistance of galvanometer $G=75/15=5\mathrm{\Omega }$

For conversion into a voltmeter, a high resistance should be connected in series with the galvanometer

$\begin{array}{rl}& V=I_g(G+R)=\frac{15}{1000}(5+R)\Rightarrow 150=15\frac{(5+R)}{1000}\\ & \text{ or }5+R=\frac{150\times 1000}{15}=10000\\ & \therefore R=9995\mathrm{\Omega }\end{array}$

Hence, the answer is the option (1).

Example 3: When a current of 5 mA is passed through a galvanometer having a coil of resistance 15 $\mathrm{\Omega }$ , it shows full-scale deflection. The value of the resistance to be put in series with the galvanometer to convert it into a voltmeter of range 0−10 V is

1) $1.985\times {10}^3\mathrm{\Omega }$

2) $2.045\times {10}^3\mathrm{\Omega }$

3) $2.535\times {10}^3\mathrm{\Omega }$

4) $4.005\times {10}^3\mathrm{\Omega }$

Solution:

Given,
$\begin{array}{rl}& {\mathrm{I}}_{\mathrm{g}\text{ (Galvanometer Current) }}=5\mathrm{mA}\\ & \mathrm{G}=\text{ Resistance of Galvanometer }=15\mathrm{\Omega }\end{array}$
$R=$ The value of the resistance to be put in series with the galvanometer
We know,
$\begin{array}{rl}& V=I_g(R+G)\\ & 10=5\times {10}^{-3}(R+15)\\ & 2000=R+15\end{array}$
$\Rightarrow R=1985\mathrm{\Omega }=1.985\times {10}^3\mathrm{\Omega }$

Hence, the answer is the option (1).

Example 4: A $50\mathrm{\Omega }$ resistance is connected to a battery of 5 V. A galvanometer of resistance $50\mathrm{\Omega }$ is to be used as an ammeter to measure the current through the resistance, for this, a resistance r_s is connected to the galvanometer. Which of the following connections should be employed if the measured current is within 1% of the current without the ammeter in the circuit?

1) $r_{\mathrm{s}}=0.5\mathrm{\Omega }$ in parallel with the galvanometer
2) $r_{\mathrm{s}}=0.5$ in series with the galvanometer
3) $r_{\mathrm{s}}=1\mathrm{\Omega }$ in series with the galvanometer
4) $r_{\mathrm{s}}=1\mathrm{\Omega }\mathrm{n}$ parallel with the galvanometer

Solution:

Moving coil galvanometer

It is a very sensitive instrument used to measure the small current. The galvanometer gives the deflection which is proportional to the electric current flowing through it.

Current in the circuit without an ammeter

$I=\frac{V}{R}=\frac{5v}{50\mathrm{\Omega }}=0.1A$

Allowed current with an ammeter

$\begin{array}{rl}& I^{\prime }=0.099A\\ & I^{\prime }=\frac{V}{R_{eq}}\\ & \text{ where }{R}_{eq}=50+\frac{100r_s}{100+r_s}\\ & \therefore 0.099=\frac{5}{50+\frac{100r_s}{100+r_s}}\\ & \Rightarrow 50+\frac{100}{100+r_s}=\frac{5}{0.099}\\ & \Rightarrow 100r_s=50+0.5r_s\\ & \Rightarrow r_s=0.5\mathrm{\Omega }\end{array}$

Hence, the answer is the option (1).

Example 5: The sensitivity of the galvanometer is increased by :

1) Increasing no. of turns

2) Decreasing the Area of the coil

3) Increasing current

4) Introducing soft Iron core

Solution:

Current sensitivity

It is defined as the deflection produced in the galvanometer per unit current.

$S_i=\frac{NBA}{K}\Rightarrow S_i\propto N$

Therefore the sensitivity of the galvanometer is directly proportional to the number of turns.

Hence, the answer is the option (1).

For more information, below video can be referred to :

Summary

A moving coil galvanometer is a precise instrument used to measure small electric currents by converting them into mechanical deflections. It operates based on the torque experienced by a current-carrying coil in a magnetic field. Key parameters like current sensitivity and voltage sensitivity are crucial for its function. Practical applications include its use in analogue multimeters and its importance in scientific research, making it an indispensable tool in electronics and education.