Rain-man Problem

What is Rain Main problem?

The Rain man probelm is simple preblem of physics chapter kinematics involving relative motion concept. It describes how the velocity and direction of rain change when a person walks or runs. The faster one moves, the more rain appears to hit him/her from the front. This then gives us an understanding of whether one would remain drier in the rain if he/she walks compared to running.

Rain man Problems Formula

When rain is falling vertically with speed $\vec{v}_R$, and a person (observer) is moving horizontally with speed $\vec{v}_m$, the rain appears to come at an angle to the person.

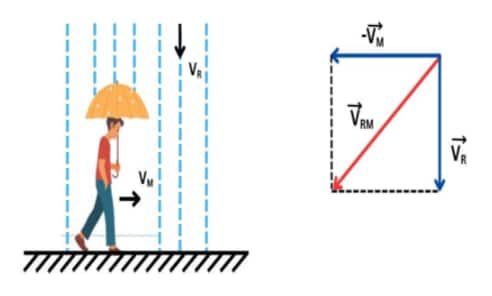
The relative velocity of rain with respect to the person is:

$\vec{v}_{R m}=\vec{v}_R-\vec{v}_m \quad$

or,

$\quad V_{R m}=\sqrt{V_R^2+V_m^2}$

The direction of the rain (angle $\theta$ ) with respect to the vertical is:

$
\theta=\tan ^{-1}\left(\frac{v_m}{v_R}\right)
$
This means the faster the person moves, the more the rain appears to slant toward their face.

Terminology

$
\begin{aligned}
& \overrightarrow{V_m}=\text { velocity of man in the horizontal direction } \\
& \overrightarrow{V_r}=\text { velocity of rain w.r.t ground } \\
& \overrightarrow{V_{r m}}=\text { velocity of rain w.r.t man }
\end{aligned}$

Recommended Topic Video

How to Solve Rain Main Problem

To solve a rain-man problem, which is a type of relative velocity problem in physics, follow these steps:

Problem Explanation

In a rain-man problem, the goal is to calculate either the angle at which a person (or object) should hold an umbrella or the velocity of the rain relative to the person. This typically involves understanding the velocities of the rain relative to the ground and the person relative to the ground.

Step-by-Step Solution

1. Identify Given Quantities

• Velocity of the rain with respect to the ground: $v_r$
• Velocity of the man with respect to the ground: $v_m$
• Angle at which the rain is falling (relative to the vertical direction): $\theta_r$

2. Set Up the Coordinate System

• Assume the ground as the reference point.
• Let the rain's velocity $v_r$ have two components: vertical $\left(v_{r_y}\right)$ and horizontal $\left(v_{r_x}\right)$.

3. Break Down Velocities into Components

• If the rain is falling at an angle, decompose its velocity:
• Vertical component of rain's velocity: $v_{r_y}=v_r \cos \left(\theta_r\right)$
• Horizontal component of rain's velocity: $v_{r_x}=v_r \sin \left(\theta_r\right)$

4. Relative Velocity of Rain with Respect to the Man

The relative velocity of the rain with respect to the man is calculated using the vector sum of the rain's velocity and the man's velocity. Since the man is moving horizontally (say with velocity $v_m$ ):

• Horizontal relative velocity: $v_{r_{\text {relative }_x}}=v_{r_x}-v_m$ component)

5. Calculate the Resultant Velocity of Rain Relative to the Man

• The resultant relative velocity can be found using the Pythagorean theorem.

6. Find the Angle at which the Man Should Hold the Umbrella

• The angle $\theta_{\text {relative }}$ at which the man should hold the umbrella (relative to the vertical) can be found using:

$\tan \left(\theta_{\text {relative }}\right)=\frac{v_{r_{\text {relative }, z}}}{v_{r_{\text {relative }, y}}}$

Also Check-

Rain Main Problem NEET/JEE Main Questions with solutions

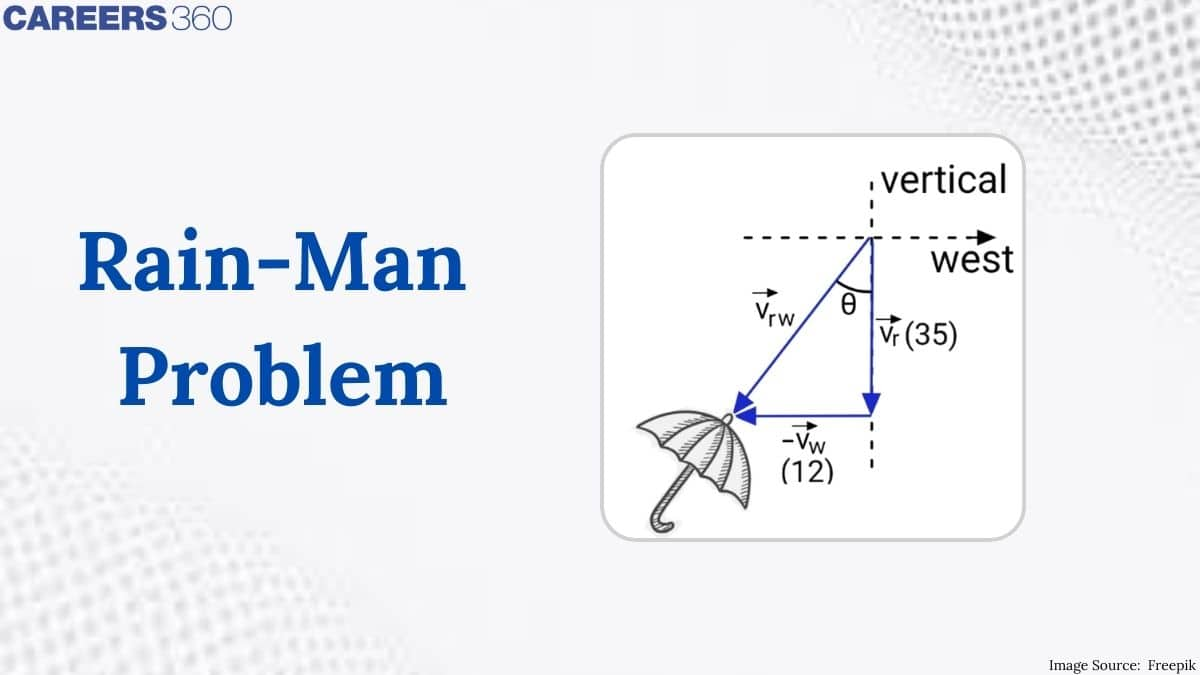
Example 1: Rain is falling vertically at a speed of 35 m/s. The wind started blowing after some time with a speed of 12 m/s in an east-to-west direction. In which direction should a boy waiting at a bus stop hold his umbrella with the vertical?

1) $\sin ^{-1}\left(\frac{12}{35}\right)$
2) $\cos ^{-1}\left(\frac{12}{35}\right)$
3) $\tan ^{-1}\left(\frac{12}{35}\right)$
4) $\cot ^{-1}\left(\frac{12}{35}\right)$

Solution:

Given,

velocity of rain - $\left|\overrightarrow{v_r}\right|=35 \mathrm{~m} / \mathrm{s}$
velocity of wind $\left|\overrightarrow{v_w}\right|=12 \mathrm{~m} / \mathrm{s}$
the velocity of rain concerning the wind-

$
\overrightarrow{v_{r w}}=\overrightarrow{v_r}-\overrightarrow{v_w}
$
vector diagram in vertical plane-

The man at rest will hold an umbrella opposite to the velocity of rain when wind is not present. In case there is wind blowing, the umbrella should be opposite to the direction of the velocity of rain concerning the wind, as shown in the figure.

$\begin{aligned} & \quad \tan \theta=\frac{V_w}{V_r}=\frac{12}{35} \\ & \therefore \theta=\tan ^{-1} \frac{12}{35}\end{aligned}$

Example 2: Rain is falling vertically downward with a velocity of 3kmph. A boy walks in the rain with a velocity of 4 mph. Traindropsops appear to be falling on the boy with a velocity (in kmph) of

1 )5

2) 3

3) 4

4) 1

Solution:

Given-

Assuming the vertical downward direction to be along y direction and horizontal direction to be x direction.

velocity of rain $=3 \hat{j}$
the velocity of the oy $=4 \hat{i}$

$
\begin{aligned}
& \vec{V}_{R B}=\vec{V}_R-\vec{V}_B \\
& =3 \hat{j}-4 \hat{i} \\
& \left|\vec{V}_{R B}\right|=\sqrt{(3)^2+(4)^2}=5 \mathrm{kmph}
\end{aligned}
$
Hence, the answer is option (1).

Example 3: When a car is at rest, its driver sees raindrops falling on it vertically. When driving the car with speed $v$, he sees that raindrops are coming at an angle of $60^{\circ}$ from the horizontal. On further increasing the car's speed to $(1+\beta) v$, this angle changes to $45^{\circ}$. The value is close to :

1) 50

2) 41

3) 37

4) 73

Solution:

Rain is falling vertically downwards.

$
\overrightarrow{\mathrm{v}}_{r / \mathrm{m}}=\overrightarrow{\mathrm{v}}_{\mathrm{r}}-\overrightarrow{\mathrm{v}}_m
$

$\begin{aligned} & \tan 60^{\circ}=\frac{\mathrm{v}_{\mathrm{r}}}{\mathrm{v}_{\mathrm{m}}}=\sqrt{3} \\ & \mathrm{v}_{\mathrm{r}}=\mathrm{v}_{\mathrm{m}} \sqrt{3}=\mathrm{v} \sqrt{3} \\ & \text { Now, } \mathrm{v}_{\mathrm{m}}=(1+\mathrm{B}) \mathrm{v} \\ & \text { and } \theta=45^{\circ} \\ & \tan 45=\frac{\mathrm{v}_{\mathrm{c}}}{\mathrm{v}_{\mathrm{m}}}=1 \\ & \mathrm{v}_{\mathrm{r}}=\mathrm{v}_{\mathrm{m}} \\ & \mathrm{v} \sqrt{3}=(1+\beta) \mathrm{v} \\ & \sqrt{3}=1+\beta \\ & \Rightarrow \beta=\sqrt{3}-1=0.73 \\ & 100 \beta=73\end{aligned}$

Example 4: A man walking at a speed of 4 km/hr finds the raindrops falling vertically downwards. When the man increases his speed to 8 km/hr he finds that the raindrops are falling making an angle of 30 degrees with the vertical. find the speed of the raindrops.

1) 4 m/s

2) 5 m/s

3) 8 m/s

4) 10 m/s

Solution:

$\overrightarrow{V_m}=$ velocity of man in the horizontal direction

$
\begin{aligned}
& \vec{V}_r=\text { velocity of rain w.r.t ground } \\
& \overrightarrow{V_{r m}}=\text { velocity of rain w.r.t man }
\end{aligned}
$

The velocity of rain w.r.t man is given by

$
\begin{aligned}
\overrightarrow{V_{r m}}=\overrightarrow{V_r}-\overrightarrow{V_m} \\
\text { As } \overrightarrow{V_{r m}}=\overrightarrow{V_r}-\overrightarrow{V_m}
\end{aligned}
$
Initially

$
V_m=4 \vec{i}
$
As $V_{r m}$ is vertically downwards and perpendicular to $V_m$

$
\tan \phi=\tan 30=\frac{4}{x}
$

So from figure $x=4 \sqrt{3}$
And $\mathrm{x}=$ vertical component of $V_r$
From the figure, the Horizontal component of $V_r=4 \mathrm{~m} / \mathrm{s}$

$
\text { So } V_r=\sqrt{4^2+(4 \sqrt{3})^2}=8 \mathrm{~m} / \mathrm{s}
$

Example 5: A man wearing a hat of extended length 12 cm is running in rain falling vertically downwards with a speed of 10 m/s. The maximum speed with which man can run, so that raindrops do not fall on his face (the length of his face below the extended part of the hat is 16 cm) will be : (please give your answer in m/s)

1) 7.5

2)13.33

3)10

4)0

Solution:

for Rain-Man Problem
$
\tan \theta=\frac{V_m}{V_r}
$

$\theta=$ angle which relative velocity of rain with
respect to man makes with the vertical
- wherein
$\vec{V}_r=$ velocity of rain falling vertically
$\overrightarrow{V_m}=$ velocity of man in the horizontal direction

$
V_{R / G(x)}=0, V_{R / G(y)}=10 \mathrm{~m} / \mathrm{s}
$
Let, the velocity of man $=V$

$
\tan \theta=\frac{16}{12}=\frac{4}{3}
$

then, $\quad V_{R / \operatorname{man}}=V_{\text {(opposite to man) }}$
For the required conditions:

$
\tan \theta \frac{V_{R / M(y)}}{V_{R / M(x)}}=\frac{10}{V}=\frac{4}{3}
$

$\begin{aligned}
&\Rightarrow V=\frac{10 \times 3}{4}=7.5\\
&\text { Hence, the answer is } 7.5 \text {. }
\end{aligned}$

The Rain Man Problem class 11 is a physics puzzle that helps to understand how getting wet in the rain depends on movement. One of the major examples of how getting wet in the course of walking or running changes is the direction and speed of the raindrops hitting you. When you are standing still doing nothing, the rain is falling vertically straight on you. The impression is that, in the process of walking or running, the rain comes at an angle, say, at an angle of 45°, and you might get more rain on the front.

The relative motion learning from such a problem is the way movements are combined. You move faster and you run into more rain from the front, so you get wetter at that spot. The potential of that idea comes into play in the real world in how to decide between walking and running in the rain too to become less wet. We make out from such practical applications that the principles of physics are ingrained in our daily routines in such a way that they help one understand how a person moves about natural phenomena.

Releated Study Resource,