Refractive Index - Formula, Definition, Uses, FAQs
Light refraction can be noticed in many places in our daily lives. It distorts the perspective of items beneath the water's surface, making them appear closer than they are. Refraction of light provides the foundation for optical lenses, which allow tools like glasses, cameras, binoculars, simple microscopes, and the human eye to function. Let's read the below article for more details regarding refractive index.

What is Refractive Index?
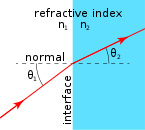
The refractive index $n$ of a medium is the ratio of the speed of light in a vacuum (c) to the speed of light in that medium $(v)$ :
$$
n=\frac{c}{v}
$$
Where:
- $n$ is the refractive index of the medium
- $c$ is the speed of light in a vacuum (about $3 \times 10^8 \mathrm{~m} / \mathrm{s}$ )
- $v$ is the speed of light in the material
The refractive index is a measurement of how much light speed varies as it enters a medium from the air. The refractive index, often known as the index of refraction, is the degree to which light changes direction in two materials. In other words, the refractive index is a measurement of how much a light beam bends as it travels from one medium to another.
Also read -
- NCERT Exemplar Solutions for All Subjects
- NCERT Notes For All Subjects
- NCERT Solutions for All Subjects
Refractive Index of Water
Water has a refractive index of 1.3, while glass has a refractive index of 1.5. We know that the refractive index of a medium is inversely proportional to the velocity of light in that medium because of equation n = c/v. As a result, light travels quickly through water.
Refractive Index of Air
Since the index of refraction of air is 1.0003, which is quite similar to the refractive index in vacuum (1.0000), these indices are often used interchangeably in most problems.
Refraction Index of Glass
Glass has a refractive index of 1.5. The speed of light in glass is 1.5 times slower than in vacuum. The speed of light in glass is not independent of light color.
Refractive Index of Prism
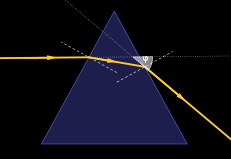
The refractive index of the prism is 1.414.
|
Related Topics |
The Refraction Phenomenon is divided into two parts:
- In the medium, the light travels at a certain speed
- Refraction Angle
Speed of light in different mediums
In a vacuum with a refractive index of 1.0, light travels at over 300,000 km per second, but it slows down to 225,000 km per second in water along with 200,000 km per second in glass.
What effect does wavelength have on the refractive index?
The speed of light is defined as the product of frequency and wavelength. Regardless of the medium, the frequency of the light wave remains constant. The wavelength of a light wave changes as a result of refraction. As a result, the refractive index of water changes as the wavelength increases.
Uses of the Refraction Index
- Mirrors and Optical Devices: The refractive index plays a central role in defining how total internal reflection occurs in optical elements such as optical fibers, prisms, and binoculars.
- Optical Fibers: Total internal reflection as a principle is used in fiber optic cables used in industries for internet connections and other communication.
- Water Quality Testing: The refractive index of the water is useful to demonstrate its purity or the presence of impurities.
- Lens Design: In photography and cinematography, lenses with specific refractive indices are designed to minimize distortions.
Frequently Asked Questions (FAQs)
The refractive index symbol is a measurement of how far a light beam bends when travelling through a medium. It's also known as n = c/v, which is the ratio of a light ray's velocity in empty space to the velocity of light in a matter.
The following formula can be used to calculate a medium's refractive index:
n=C/v
where n is the medium's refractive index.
The speed of light in vacuum is c.
v denotes the speed of light in the medium.
In water, light travels at a faster rate. Water has a refractive index of 1.3, while glass has a refractive index of 1.5. As we know that refractive index of medium is inversely proportional to velocity of light medium because of the equation
n=C/v. As a result, light travels quicker through water.
Since the units cancel out while calculating the value, the refractive index has no units. Divide the speed by the refractive index to get the refractive index.
It sparks a lot because it has a high refractive index, which means that light entering the diamond's structure is completely internally reflected many times, resulting in a lot of light rays departing in all directions. The refractive index of diamond is 2.4. (air has 1).