Relation Between Elastic Constants

Relation Between Elastic Constants - A Complete Guide

Edited By Team Careers360 | Updated on Jul 02, 2025 04:44 PM IST

Key points of this article:-

Elastic constant
Relation between young’s modulus and bulk modulus
Relation between modulus of elasticity and modulus of rigidity
Relation between young's modulus, bulk modulus and Poisson’s ratio
Relation between young's modulus and shear modulus
Relation between young’s modulus bulk modulus and modulus of rigidity.
What is elastic constants
Definition of elastic constant

Now, discuss the elastic constant and their relationship

What is elastic constant:- We can define elastic constant as Elastic constants are constants which tell us the elastic behaviour of materials.

This is the elastic constant definition

There are three elastic constants (or elastic coefficients)

Young’s modulus of elasticity (Y or E) = longitudinal stress / longitudinal strain

Bulk modulus of elasticity (K) = Normal stress/ volume strain

Modulus of rigidity/bulk modulus of rigidity (η or G) = tangential stress/ shearing stress

Poission’s ratio :- The ratio between decreasement per unit length and per unit force and the increasement per unit length and per unit force is called poissions’s ratio.

σ = 1.1.β/1.1.α

Where β = the decreasement in length

α = the increasement in length

Relation between young’s modulus, bulk modulus and Poisson's ratio:-

Let us consider a cube whose side is unit length to derive the relation between Y, K and σ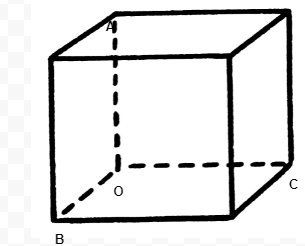

I.e., OA = OB = OC = 1

So, the volume of the cube

V = 1 (without normal stress)

Also read -

When a normal stress is applied on a every face of cube so the increasement in unit length is α and decreasement is β due to unit force.

So, the side of the cube

OA = 1 + F.1.α - F.1.? - F.1.?

= 1 + F.α - 2F?

= 1 + F ( α - 2? )

So, OA = OB = OC = 1 + F ( α - 2? )

Then the volume of the cube

V’ = OA.OB.OC

= [1 + F ( α - 2? )]³

V’ = [ 1 + 3F ( α - 2? )]

So, change in the volume of the cube

ΔV = V’ - V

= 1 + 3F(α - 2? ) - 1

ΔV = 3F(α - 2? )

And the volume strain of the cube = change in volume/initial volume

= ΔV/V = 3F(α - 2? )/1

= 3F(α - 2? )

And the bulk modulus of elasticity of the cube (K) = normal stress/normal strain

= Force/area/ΔV/V = F/1/3F(α - 2? )

K = 1/3(α - 2? ) = 1/3α(1 - 2?/α)

= 1/α/3(1 - 2σ) ( ∵ σ = β/α)

K = Y / 3 ( 1 - 2σ)

∵ Y = long. stress/long. Strain

Y = F/A/Δl/l = F/1/F.1.α/1 = 1/α

Y = 3K( 1 - 2σ)

……(A)

Relation between E and K is

E = 3K( 1 - 2σ)

This is the relation between elastic constants- relation between young modulus and bulk modulus and poisson ratio/ relation between bulk modulus and young’s modulus.

Related Topics Link,

Relation between relation between young's modulus and modulus of rigidity

For derive the relation between elastic constants - Young’s modulus (Y), modulus of rigidity (η) and the poission’s ratio. Considered a face of cube ABCD side of this face is L. Fixed the side CD and applied the tangential stress (T) on the side AD due to to this A and B point is displaced linearly (l) distance and angularly ? angle and obtained a new position A’ and B’.

So, tangential stress on the side AB

T = force/area = F/L²

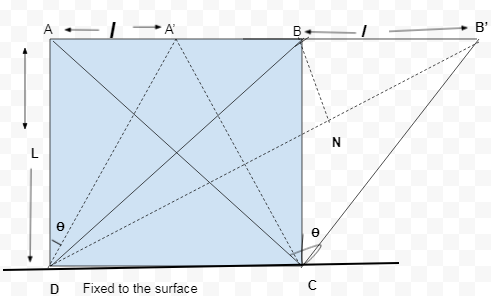
Relation between relation between young's modulus and modulus of rigidity

And shearing strain

tan? = l/L

But ? is very small tan? ∝ ?

? = l/L

So, the modulus of rigidity of face ABCD

η = T/?

η = F/l²/l/L

η = F/lL …..(i)

NCERT Physics Notes:

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Due to tangential stress T diagonal BD of ABCD face changes to B’D. To determine the change of diagonal BD to B’D a perpendicular line is drawn which cut at N point. In this position, NB’ diagonal represent the increment in the B’D diagonal.

In ΔBNB’

Cos45° = NB’/BB’

NB’ = lcos45°

NB’ = l/√2 ….(ii)

This eqn shows that the increment in the diagonal

Due to tangential stress T increments in the BD diagonal and decrement in AC diagonal. Due to unit force increment and decrement in unit length is represented by

α and β.

Due to tangential stress T increasement in BD diagonal = T.BD.α

= F/L².L√2.α

= F/L.√2.α

Due to tangential stress T decreasement in AC diagonal = T.AC.?

= F/L².L√2.?

= F/L.√2.?

So, the total change in the diagonals of ABCD face = F/L.√2.α + F/L.√2.?

= F√2/L (α + ? ) ….(iii)

From equation (ii) and (iii)

l/√2 = F√2/L (α + ? )

F/lL = 1/2(α + ? )

F/lL = 1/2α(α + ?/α) (∵ σ = ?/α)

F/lL = 1/2α(1 + σ)

From eqn (i)

η = 1/α/2(1 + σ ) ( ∵ Y = 1/α)

η = Y/2(1 + σ )

Y = 2η(1 + σ)

…….(B)

This is the relation between young modulus and shear of modulus ( or modulus of rigidity ).

And the relation between young’s modulus modulus of rigidity and Poisson’s ratio/ relation between young's modulus and poisson's ratio.

Relation between E and G is

E = 2G(1 + σ)

This is the relation between elastic constants- relation between young’s modulus and rigidity modulus

Relation between Bulk modulus, Modulus of rigidity and Poisson’s ratio:-

From eqn (A) and (B)

2η(1 + σ) = 3K(1 - 2σ)

2η + 2ησ = 3K - 6Kσ

6Kσ + 2ησ = 3K - 2η

σ( 6K + 2η) = 3K - 2η

σ = 3K - 2η/6K + 2η

………(C)

Also read :

This is the relation between bulk modulus of elasticity, poission’s ratio and modulus of

elasticity/ relation between elastic constants.

Relation between Young’s modulus bulk modulus and modulus of rigidity:-

From eqn (A)

Y = 3K ( 1 - 2σ )

Y/3K = 1 - 2σ

σ = 1/2 - Y/6K …….(a)

From eqn (B)

Y = 2η(1 + σ)

Y/2η = (1 + σ)

σ = Y/2η -1 ………(b)

From eqn (1) and (2)

1/2 - Y/6K = Y/2η -1

Y/2η + Y/6K = 1/2 + 1

Y[ 1/2η + 1/6K] = 3/2

Y/2 [1/η + 1/3K] = 3/2

3/η + 1/K = 9/Y

……(D)

or, Y = 9Kη/3K + η

This is the relation between elastic constants Young’s modulus, bulk modulus and modulus of rigidity.

Relation between E, G and K Young’s modulus, Bulk modulus and Modulus of rigidity is

E = 9KG/3K + G .

These are the elastic constant formula and elastic constants relation.

Also check-

Frequently Asked Questions (FAQs)

1. What is the relation between shear modulus and young's modulus?

Relation between shear modulus and young’s modulus is

Y = 2η(1 + σ)

2. What is the relation between the modulus of elasticity and bulk modulus?

Relation between modulus of elasticity and bulk modulus or relation between elastic modulus and bulk modulus is

Y = 3K( 1 - 2σ)

3. What is the relation between E and G

Relation between E and G is

3/G + 1/K = 9/E

E = 9KG/3K + G

4. What is the relation between poisson ratio and young's modulus?

Y = 2η(1 + σ)

This is the relation between elastic constant - Young’s modulus and Poisson’s ratio.

5. What is the relation between bulk modulus and modulus of rigidity?

σ = 3K - 2η/6K + 2η

Where K = bulk modulus and η = modulus of rigidity.

6. What are elastic constants and why are they important in physics?

Elastic constants are parameters that describe how a material deforms under stress and returns to its original shape when the stress is removed. They are important in physics because they help us understand and predict the behavior of materials under different types of forces, which is crucial in engineering, construction, and material science.

7. How many independent elastic constants does an isotropic material have?

An isotropic material, which has uniform properties in all directions, has only two independent elastic constants. These are typically expressed as Young's modulus and Poisson's ratio, or alternatively as bulk modulus and shear modulus. All other elastic constants can be derived from these two.

8. What is the relationship between Young's modulus (E) and shear modulus (G)?

For an isotropic material, Young's modulus (E) and shear modulus (G) are related by the equation: E = 2G(1 + ν), where ν is Poisson's ratio. This relationship demonstrates that these constants are not independent but are interconnected through material properties.

9. How does Poisson's ratio relate to the compressibility of a material?

Poisson's ratio (ν) is inversely related to a material's compressibility. Materials with a higher Poisson's ratio are less compressible, while those with a lower Poisson's ratio are more compressible. The theoretical limits for Poisson's ratio are -1 and 0.5, with most materials falling between 0 and 0.5.

10. Can Poisson's ratio be negative? If so, what does this mean?

Yes, Poisson's ratio can be negative, although it's rare. Materials with negative Poisson's ratio are called auxetic materials. When stretched, these materials become thicker perpendicular to the applied force, unlike most materials which become thinner. This unusual property can lead to enhanced mechanical properties in certain applications.

11. What is the bulk modulus and how is it related to compressibility?

The bulk modulus (K) is a measure of a material's resistance to uniform compression. It is inversely related to compressibility: K = 1 / compressibility. Materials with a high bulk modulus are less compressible and vice versa. This relationship is crucial in understanding how materials behave under hydrostatic pressure.

12. How are Young's modulus (E) and bulk modulus (K) related?

Young's modulus (E) and bulk modulus (K) are related through Poisson's ratio (ν) by the equation: E = 3K(1 - 2ν). This relationship shows that for a given material, knowing any two of these three constants allows us to calculate the third.

13. What is Lame's first parameter (λ) and how is it related to other elastic constants?

Lame's first parameter (λ) is an elastic constant that, along with the shear modulus, can describe the elastic behavior of isotropic materials. It's related to other constants by: λ = K - (2/3)G, where K is the bulk modulus and G is the shear modulus. It's less commonly used but can be useful in certain theoretical analyses.

14. How does the ratio of longitudinal to transverse strain define Poisson's ratio?

Poisson's ratio (ν) is defined as the negative of the ratio of transverse strain to longitudinal strain. Mathematically, ν = -(εtransverse / εlongitudinal). This means that when a material is stretched, Poisson's ratio describes how much it contracts in the perpendicular directions.

15. Why do most materials have a Poisson's ratio between 0.2 and 0.5?

Most materials have a Poisson's ratio between 0.2 and 0.5 due to the nature of their atomic or molecular structures. This range reflects the balance between the material's resistance to volume change (bulk modulus) and its resistance to shape change (shear modulus). A Poisson's ratio of 0.5 represents the upper limit for a stable, isotropic material and indicates incompressibility.

16. What happens to a material's volume when it's subjected to uniaxial stress?

When a material is subjected to uniaxial stress, its volume generally changes. The change in volume depends on the material's Poisson's ratio. For most materials with a positive Poisson's ratio, the volume increases slightly under tensile stress and decreases under compressive stress. However, for a perfectly incompressible material (Poisson's ratio = 0.5), the volume remains constant.

17. How does the relationship between elastic constants change for anisotropic materials?

For anisotropic materials, which have properties that vary with direction, the relationships between elastic constants become more complex. Instead of just two independent constants, anisotropic materials can have up to 21 independent elastic constants, depending on their symmetry. The relationships between these constants are described by tensors rather than simple scalar equations.

18. What is the physical significance of the shear modulus?

The shear modulus (G) represents a material's resistance to shear deformation. It describes how much a material resists changing shape when subjected to a shear stress. Materials with a high shear modulus are more resistant to shape changes under stress, while those with a low shear modulus deform more easily. This property is crucial in understanding how materials behave under torsion or sliding forces.

19. How does temperature affect the elastic constants of a material?

Temperature generally affects elastic constants by changing the interatomic forces within the material. As temperature increases, most materials become less stiff, resulting in a decrease in elastic constants like Young's modulus and shear modulus. However, the exact relationship can be complex and material-specific, sometimes involving phase transitions or other structural changes at certain temperatures.

20. What is the significance of the ratio E/G (Young's modulus to shear modulus)?

The ratio E/G is significant because it's directly related to Poisson's ratio: E/G = 2(1 + ν). This relationship provides insight into a material's behavior under different types of stress. A higher E/G ratio indicates a material that is more resistant to axial deformation relative to shear deformation, which is characteristic of materials with a higher Poisson's ratio.

21. How do elastic constants relate to the speed of sound in a material?

Elastic constants are directly related to the speed of sound in a material. For longitudinal waves in a solid, the speed of sound (v) is given by v = √(E/ρ), where E is Young's modulus and ρ is the density. For transverse waves, it's v = √(G/ρ), where G is the shear modulus. These relationships show how the stiffness of a material affects wave propagation.

22. What is the bulk modulus of a perfectly incompressible material?

A perfectly incompressible material would have an infinite bulk modulus. This is because the bulk modulus (K) is defined as the ratio of pressure change to the resulting relative change in volume: K = -V(dP/dV). For an incompressible material, dV = 0 for any applied pressure, leading to an infinite K. In reality, no material is perfectly incompressible, but some liquids come close.

23. How does the concept of elastic constants apply to non-linear elastic materials?

For non-linear elastic materials, the concept of elastic constants becomes more complex. Instead of constant values, the elastic properties vary with the amount of deformation. In these cases, we often use tangent moduli or secant moduli, which describe the instantaneous or average stiffness over a range of deformation. The relationships between these variable moduli are more complicated and often require numerical methods to analyze.

24. What is the relationship between Young's modulus and the spring constant in Hooke's law?

Young's modulus (E) is related to the spring constant (k) in Hooke's law through the geometry of the object. For a rod or wire under axial stress, k = AE/L, where A is the cross-sectional area and L is the length. This shows that the spring constant is not just a material property but also depends on the object's dimensions, while Young's modulus is an intrinsic material property.

25. How do elastic constants relate to a material's ability to store elastic energy?

Elastic constants directly relate to a material's ability to store elastic energy. The strain energy density (energy stored per unit volume) is proportional to the square of the strain and the relevant elastic constant. For example, under uniaxial stress, the strain energy density is (1/2)Eε², where E is Young's modulus and ε is the strain. Materials with higher elastic constants can store more elastic energy for a given deformation.

26. What is the physical meaning of Lame's second parameter, and how is it related to the shear modulus?

Lame's second parameter is actually identical to the shear modulus (G). It represents the material's resistance to shear deformation. The use of Lame's parameters (λ and G) can simplify some equations in elasticity theory, especially when dealing with stress-strain relationships in three dimensions.

27. How do elastic constants influence the bending of beams?

Elastic constants, particularly Young's modulus (E), play a crucial role in beam bending. The flexural rigidity of a beam, which determines its resistance to bending, is given by EI, where I is the second moment of area of the beam's cross-section. A higher Young's modulus results in a stiffer beam that deflects less under a given load.

28. What is the significance of the ratio of bulk modulus to shear modulus (K/G)?

The ratio of bulk modulus to shear modulus (K/G) provides insight into a material's relative resistance to volume change versus shape change. A high K/G ratio indicates a material that resists volume change more than shape change, which is characteristic of liquids and rubber-like materials. Conversely, a low K/G ratio is typical of materials that maintain their shape but are more compressible, like cork.

29. How do elastic constants relate to the concept of strain energy?

Elastic constants are directly related to strain energy, which is the energy stored in a material due to elastic deformation. The strain energy density (U) for different types of deformation is expressed in terms of elastic constants and strains. For example, for uniaxial stress, U = (1/2)Eε², where E is Young's modulus and ε is the strain. This relationship shows how stiffer materials (higher E) store more energy for a given strain.

30. What is the Pugh's ratio and what does it tell us about a material?

Pugh's ratio is defined as the ratio of shear modulus to bulk modulus (G/K). It provides information about a material's ductility or brittleness. Materials with a high Pugh's ratio (typically > 0.57) tend to be more brittle, while those with a low Pugh's ratio are generally more ductile. This ratio is useful in predicting material behavior in applications where toughness is important.

31. How do elastic constants influence the propagation of elastic waves in solids?

Elastic constants directly affect the speed and behavior of elastic waves in solids. The speed of longitudinal waves is related to both the bulk modulus and shear modulus, while the speed of transverse waves depends only on the shear modulus. The ratio of these speeds can be used to determine Poisson's ratio. Additionally, the reflection and transmission of waves at interfaces depend on the elastic constants of the materials involved.

32. What is the relationship between elastic constants and a material's fracture toughness?

While elastic constants don't directly determine fracture toughness, they play a role in it. Materials with higher elastic moduli tend to have higher stress concentrations at crack tips, which can lead to lower fracture toughness. However, the relationship is complex and also involves factors like plastic deformation and atomic bonding. Generally, a balance of high stiffness and ability to deform plastically leads to good fracture toughness.

33. How do elastic constants relate to the concept of resilience in materials?

Resilience is a material's ability to absorb energy when deformed elastically and release that energy upon unloading. It's directly related to the elastic constants, particularly Young's modulus. The modulus of resilience, which quantifies this property, is given by the area under the stress-strain curve up to the yield point. For linear elastic materials, it's expressed as σ²y / (2E), where σy is the yield stress and E is Young's modulus.

34. What is the significance of the Poisson function in anisotropic materials?

In anisotropic materials, the Poisson function replaces the single Poisson's ratio used for isotropic materials. It describes how strain in one direction relates to strains in perpendicular directions and can vary depending on the direction of applied stress. Understanding the Poisson function is crucial for accurately predicting the behavior of anisotropic materials under complex stress states.

35. How do elastic constants influence the buckling behavior of columns?

Elastic constants, particularly Young's modulus (E), play a crucial role in column buckling. The critical buckling load for a column is directly proportional to EI, where I is the moment of inertia of the column's cross-section. A higher Young's modulus results in a higher critical buckling load, meaning the column can support more weight before buckling occurs.

36. What is the relationship between elastic constants and the speed of Rayleigh waves on a material's surface?

Rayleigh waves are surface waves that travel along the boundary of an elastic medium. Their speed is related to the shear wave speed, which in turn depends on the shear modulus and density of the material. The exact relationship involves a complex function of Poisson's ratio, but in general, materials with higher shear moduli and lower densities will have faster Rayleigh waves.

37. How do elastic constants affect the natural frequencies of vibration in structures?

Elastic constants, particularly Young's modulus (E), directly influence the natural frequencies of vibration in structures. For simple systems like beams or plates, the natural frequencies are proportional to √(E/ρ), where ρ is the density. Stiffer materials (higher E) lead to higher natural frequencies, while denser materials lower the frequencies. This relationship is crucial in designing structures to avoid resonance.

38. What is the bulk modulus of a gas, and how does it differ from that of solids?

The bulk modulus of a gas is equal to its pressure for an isothermal process. Unlike solids, where the bulk modulus is typically constant (for small deformations), the bulk modulus of a gas changes with pressure. This variable nature of gas bulk modulus is due to the large compressibility of gases compared to solids and liquids.

39. How do elastic constants relate to the concept of acoustic impedance?

Acoustic impedance, which is important in the study of sound transmission, is related to elastic constants. For longitudinal waves, the acoustic impedance is given by Z = √(Eρ), where E is Young's modulus and ρ is density. This shows that materials with higher stiffness and density have higher acoustic impedance, affecting how sound waves are transmitted and reflected at interfaces.

40. What is the significance of the Cauchy relation in elastic theory?

The Cauchy relation states that for certain materials, the elastic constants are related such that C12 = C44, where C12 and C44 are elements of the elastic stiffness tensor. This relation simplifies the elastic behavior to depend on only two independent constants. While not universally applicable, it holds for some simple crystal structures and can be useful in theoretical analyses.

41. How do elastic constants influence the behavior of composite materials?

In composite materials, the overall elastic constants depend on the properties and arrangement of the constituent materials. Various models, such as the rule of mixtures or more complex homogenization techniques, are used to predict the effective elastic constants of composites. Understanding these relationships is crucial for designing composites with specific mechanical properties.

42. What is the relationship between elastic constants and thermal expansion coefficients?

While not directly related, elastic constants and thermal expansion coefficients are both influenced by interatomic forces. Generally, materials with stronger interatomic bonds (and thus higher elastic constants) tend to have lower thermal expansion coefficients. However, this relationship is not strict, and exceptions exist. The Grüneisen parameter provides a more formal link between these properties.

43. How do elastic constants change near a material's melting point?

As a material approaches its melting point, its elastic constants generally decrease. This is due to the weakening of interatomic bonds and increased atomic mobility. The rate of decrease often accelerates near the melting point, and some elastic constants (like the shear modulus) may approach zero as the material transitions to a liquid state.

44. What is the significance of the third-order elastic constants?

Third-order elastic constants describe the nonlinear elastic behavior of materials under large deformations. They become important when the stress-strain relationship deviates from linearity. These constants are crucial for understanding phenomena like acoustic nonlinearity, shock wave