Spherical Mirror Formula - Characteristics, Table, FAQs

Edited By Team Careers360 | Updated on Jul 02, 2025 04:44 PM IST

Introduction

In this article, our focus will be on the spherical mirror, its formula, sign convention, sign convention for mirror and lenses etc.

What is a spherical mirror?

A spherical mirror is a mirror that is in the shape of a piece cut from a spherical surface.

It is of two types:-

Convex mirror
Concave mirror

This Story also Contains

Introduction
What is a spherical mirror?
What is a mirror formula?
Sign convention table

Spherical Mirror Formula - Characteristics, Table, FAQs

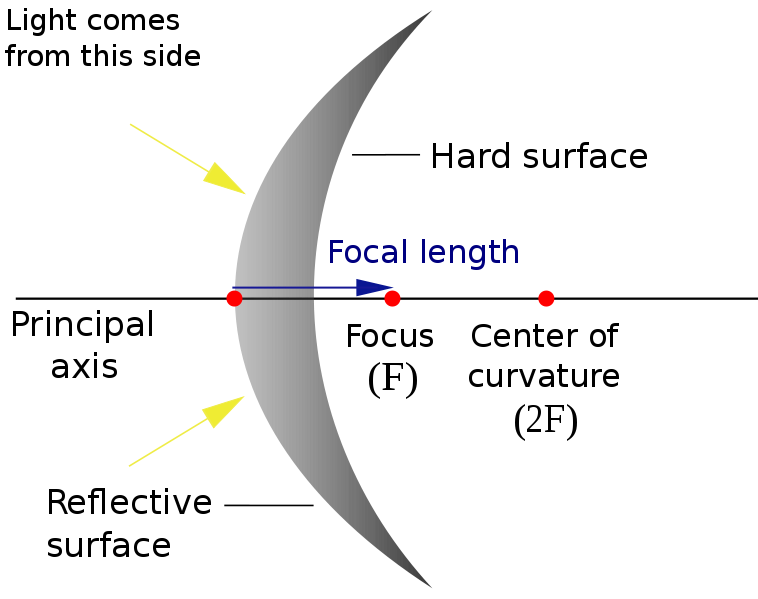
Convex mirror

Convex Mirror is a curved mirror, the reflective surface of which curves towards the light source (toward outside). These bulging surfaces reflect light outwards and are not used to focus light. These mirrors form a virtual image because the focal point (F) and the center of curvature (2F) are imaginary points on the mirror that cannot be reached. This results in the formation of images that cannot be projected on a screen because the image is inside the mirror. The image appears smaller than the object from a distance, but becomes larger as the object gets closer to the mirror.

Characteristics :

A convex mirror is also known as a diverging mirror because this mirror scatters light when it hits its reflective surface.
Virtual, upright, and reduced images are always created or viewed with convex mirrors, regardless of the distance between the object and the mirror.

convex mirror diagram

Also read -

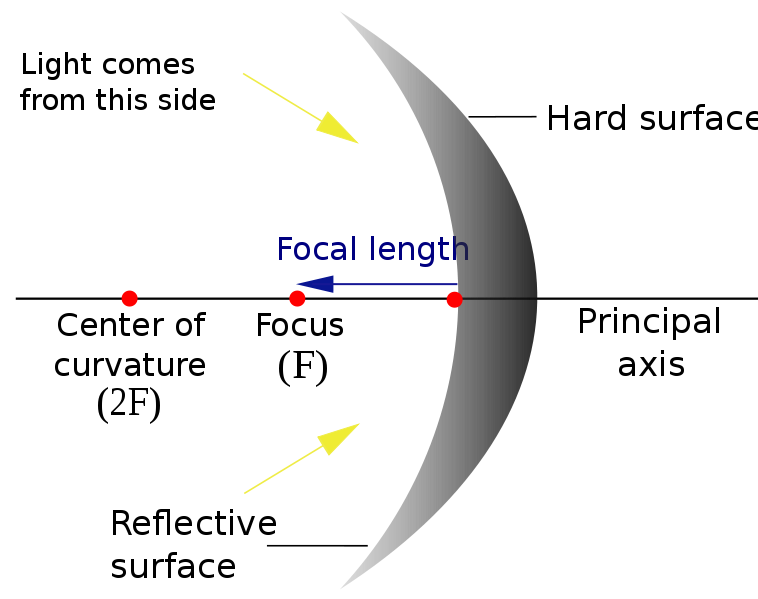
Concave mirror

We know that a section of a reflective sphere is a spherical mirror. If the reflective surface is on the inward curved side, it is a concave mirror. Concave mirrors are often used as a shaving mirror or by dentists and even in telescopes. The reflected image is enlarged, but the field of view is limited. Concave mirrors are also called collective mirrors.

Characteristics:

Light after reflection converges at a point where it hits and is reflected from the reflective surface of the concave mirror. That is why it is also known as a collective mirror.
When the collective mirror is placed very close to the object, an enlarged virtual image is observed.
It is observed that with the increase in the distance between object and the mirror, there will be a decrease in the size of the image and a real image emerges.
The image created by the concave mirror can be small or magnified, real or virtual.

concave mirror diagram

What is a mirror formula?

It is an equation that relates the distance of the object and the distance of the image to the focal length and is known as the mirror equation.

In a spherical mirror:

The distance between the object and the mirror is called the object distance (u).
The distance between the image and the mirror is called the image distance (v).
Focal length (f) is the line connecting principal focus and the mirror.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

The relation between object distance, image distance, and focal length is given as:

u be the object distance

v be the image distance

f be the focal length,

R be the spherical mirror’s radius of curvature

Related Topics Link,

What is sign convention?

The Sign Convention is a set of rules to establish signs for the distance of the image, the distance of objects, the focal length, etc.

Rules for sign convention

From the mirror the distances must be measured.
Distances measured in the direction of incidence of light must be evaluated as positive and in the opposite direction of incidence of light as negative.
Object height and image height are positive when measured from the axis up and negative when measured down.
Focal length and radius of curvature are negative for a concave mirror and positive for a convex mirror.

New cartesian sign convention/ sign convention for reflection by spherical mirror

The optical center of the lens is taken into account for the measurement of all distances.
If distances are measured in the opposite direction of incident light, they are considered negative.
If distances are measured in the same direction as the incident light, they are considered positive.
If the heights are measured upward and perpendicular to the principal axis, they are considered positive.
If the heights are measured downward and perpendicular to the principal axis, they are considered negative.

Sign convention for concave mirror

Since the object is always placed in front of the mirror, the sign of the object distance is assumed to be negative.
Since the center of curvature and the focal point are in front of the concave mirror, the signs of the radius of curvature and the focal length of the concave mirror are evaluated as negative.
When creating an image in front of the mirror, the image distance is taken as - (negative) and when creating an image behind the mirror, the image distance is taken as + (positive).
Image height is taken as positive for erect images and negative for inverted images

Sign convention for convex mirror

Since the object is always placed in front of the mirror, the sign of the object distance is assumed to be negative.
Since the center of curvature and the focal point lie behind the convex mirror, the signs of the radius of curvature and the focal length are assumed to be + (positive) for the convex mirror.
The image distance in a convex mirror is positive as the image falls back of the mirror.
A convex mirror always creates an erect image, so the image height is evaluated as positive.

Also Read:

Sign convention table

Types of lenses

Height of the image

Height of the object

Convex

Negative

Real image- positive

Virtual image- negative

Real image- Positive

No virtual focus

Real image-negative

Virtual image-positive

Positive

Concave

Negative

No real image is formed

Virtual image-negative

No real focus

Virtual image- Negative

No real image is formed

Virtual image-positive

Positive

Questions on spherical mirrors

1. The focal length and the object distance in case of a concave mirror are 3 cm and 6 cm respectively. Calculate the image distance.

Ans:

From the mirror formula,

Using sign convention for concave mirror,

u= object distance= 6cm

v= image distance

f= focal length of the concave mirror = 3 cm

putting the values,

Image distance of mirror is -6cm

2. The focal length and the object distance in case of a convex mirror are 6 cm and 8 cm respectively. Calculate the image distance.

Ans.

From the mirror formula,

Using sign convention for convex mirror,

u= object distance= 8cm

f= focal length of the convex mirror = 6 cm

putting the values,

Image distance of mirror is cm

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. What is the meaning of sign convention?

The Sign Convention is a set of rules to establish signs for the distance of the image, the distance of objects, the focal length, etc.

2. Write the rules for sign convention for spherical mirrors.

From the mirror the distances must be measured.

Distances measured in the direction of incidence of light must be evaluated as positive and in the opposite direction of incidence of light as negative.

Object height and image height are positive when measured from the axis up and negative when measured down.

Focal length and radius of curvature are negative for a concave mirror and positive for a convex mirror.

3. Write the sign convention for spherical lenses.

The optical center of the lens is taken into account for the measurement of all distances.
If distances are measured based on the direction of incident light, they are considered negative.
If distances are measured in the same direction as the incident light, they are considered positive.
If the heights are measured upward and perpendicular to the principal axis, they are considered positive.
If the heights are measured downward and perpendicular to the principal axis, they are considered negative

4. What is the magnification formula for mirror/ magnification of spherical mirror?

Magnification of concave mirror/ magnification of mirror is given by,

M=vu where v is the image distance, and u is the object distance.

5. What is the focal length of a spherical mirror?

The line connecting the pole and the principal focus of a mirror is called focal length of a spherical mirror.

6. Define lateral magnification / longitudinal magnification.

Length of image divided by the length of the object is called lateral magnification or longitudinal magnification.

7. Define angular magnification formula.

The value of angle of the image observed through the telescope divided by the angle of the same object observed in the absence of the telescope is called angular magnification.

8. Why do drivers' side mirrors on cars often use convex mirrors?

Drivers' side mirrors on cars often use convex mirrors because they provide a wider field of view, allowing drivers to see more of their surroundings. While the images appear smaller, this trade-off is beneficial for safety as it reduces blind spots. The convex shape also always produces an upright image, which is easier for drivers to interpret quickly.

9. How do parabolic mirrors differ from spherical mirrors in terms of image formation?

Parabolic mirrors focus all parallel rays to a single point, eliminating spherical aberration. Spherical mirrors, however, only approximate this for rays near the optical axis. Parabolic mirrors are ideal for applications requiring precise focusing of parallel light, like in telescopes or satellite dishes, but are more complex to manufacture than spherical mirrors.

10. How does the focal length of a spherical mirror change if it's immersed in water?

The focal length of a spherical mirror doesn't change when immersed in water or any other medium. This is because mirrors work by reflection, not refraction. The speed of light changes in different media, affecting refraction, but reflection angles remain the same regardless of the medium, so the mirror's focusing properties remain unchanged.

11. Why does a concave mirror used for makeup magnification need to be held close to the face?

A concave mirror used for makeup magnification needs to be held close to the face because it forms a magnified, virtual image only when the object (face) is between the focal point and the mirror surface. If the mirror is too far away, it will form an inverted, real image, which is not useful for makeup application.

12. Why do concave mirrors used in telescopes need to have a large radius of curvature?

Concave mirrors used in telescopes need to have a large radius of curvature (and thus a long focal length) for several reasons: 1) It reduces spherical aberration, improving image quality. 2) It allows for a higher magnification, as magnification is proportional to focal length. 3) It provides a flatter field of view, which is important for observing large areas of the sky.

13. How does the sign convention work for the spherical mirror formula?

In the sign convention for spherical mirrors, distances measured in the direction of incident light are considered positive, while those measured opposite to the direction of incident light are negative. For a concave mirror, the focal length is positive, while for a convex mirror, it's negative. Object distances are always positive, and image distances are positive for real images and negative for virtual images.

14. What's the difference between longitudinal and lateral magnification in spherical mirrors?

Longitudinal magnification refers to the ratio of the image's depth to the object's depth along the optical axis. Lateral magnification is the ratio of image height to object height perpendicular to the optical axis. In spherical mirrors, lateral magnification is given by m = -v/u, while longitudinal magnification is the square of lateral magnification.

15. How do you determine if an image formed by a spherical mirror is real or virtual without calculation?

To determine if an image is real or virtual without calculation, consider where the reflected rays intersect. If the reflected rays actually intersect, the image is real. If they only appear to intersect when traced backwards (i.e., they diverge), the image is virtual. Real images can be projected on a screen, while virtual images cannot.

16. How does the image change as an object moves from infinity towards a concave mirror?

As an object moves from infinity towards a concave mirror, the image changes as follows: At infinity, a tiny real image forms at the focal point. As the object moves closer, the image becomes larger but remains real and inverted, moving away from the mirror. When the object reaches the center of curvature, the image is the same size as the object. As it moves closer, the image becomes larger than the object. At the focal point, no image forms. Between the focal point and mirror, the image becomes virtual, upright, and magnified.

17. How does the spherical mirror formula relate to the concept of vergence in optics?

The spherical mirror formula (1/f = 1/u + 1/v) is directly related to the concept of vergence in optics. Vergence is the reciprocal of distance and is measured in diopters (m⁻¹). In the formula, 1/u represents the vergence of incident light, 1/v the vergence of reflected light, and 1/f the vergence of the mirror. The formula shows that the mirror's vergence is the sum of incident and reflected light vergences.

18. What is the spherical mirror formula and what does it represent?

The spherical mirror formula is 1/f = 1/u + 1/v, where f is the focal length, u is the object distance, and v is the image distance. This formula represents the relationship between these key parameters for both concave and convex spherical mirrors, allowing us to calculate any one of these values if we know the other two.

19. How does the spherical mirror formula relate to the lens maker's formula?

The spherical mirror formula (1/f = 1/u + 1/v) is similar to the lens maker's formula, but simpler. Both relate object distance, image distance, and focal length. However, the lens formula accounts for two refracting surfaces and the refractive index of the lens material, while the mirror formula deals with a single reflecting surface.

20. How does magnification work in spherical mirrors?

Magnification in spherical mirrors is the ratio of image height to object height, or equivalently, the ratio of image distance to object distance. It's expressed as m = hi/ho = -v/u, where hi is image height, ho is object height, v is image distance, and u is object distance. The negative sign indicates an inverted image for real images.

21. What is spherical aberration and how does it affect image formation in spherical mirrors?

Spherical aberration is an optical effect where light rays reflecting from different parts of a spherical mirror don't converge to a single focal point. This causes the image to be slightly blurred or distorted, especially for rays reflecting far from the mirror's axis. It's more pronounced in mirrors with a large aperture relative to their focal length.

22. Can you explain why a spoon's concave side produces an inverted image while its convex side produces an upright image?

The concave side of a spoon acts like a concave mirror, which can form real, inverted images when the object is beyond its focal point. The convex side acts like a convex mirror, which always forms virtual, upright images. This difference is due to how the curved surfaces reflect light rays - concave surfaces can converge rays to form real images, while convex surfaces always diverge rays.

23. Why do we use a spherical mirror instead of a flat mirror in many optical applications?

Spherical mirrors are used in many optical applications because they can focus or diverge light, unlike flat mirrors which only reflect light. This focusing ability allows spherical mirrors to form images of objects, magnify or reduce image size, and collect or spread light in ways that flat mirrors cannot, making them useful in telescopes, car headlights, and many other devices.

24. What's the difference between a real and virtual image formed by a spherical mirror?

A real image is formed when light rays actually converge at a point after reflection from the mirror. It can be projected on a screen and is always inverted. A virtual image, on the other hand, is formed when light rays appear to diverge from a point after reflection. It cannot be projected on a screen, is always upright, and is seen when looking into the mirror.

25. What is the relationship between the focal length and radius of curvature of a spherical mirror?

The focal length (f) of a spherical mirror is half of its radius of curvature (R). This relationship is expressed as f = R/2. This means that the center of curvature is twice as far from the mirror as the focal point.

26. How does the position of an object relative to the focal point affect the image formed by a concave mirror?

In a concave mirror, if the object is beyond the center of curvature, the image is real, inverted, and smaller. If it's between the center of curvature and focal point, the image is real, inverted, and larger. If it's between the focal point and the mirror, the image is virtual, upright, and larger. At the center of curvature, the image is real, inverted, and same size. At the focal point, no image is formed as rays become parallel after reflection.

27. Can a convex mirror ever form a real image?

No, a convex mirror cannot form a real image. Convex mirrors always form virtual, upright images that appear smaller than the object. This is because the reflected rays from a convex mirror always diverge, never converging to form a real image.

28. What happens to the image when you cover half of a spherical mirror?

When you cover half of a spherical mirror, the entire image is still formed, but it becomes dimmer. This is because each point on the mirror contributes to the formation of the entire image. Covering half the mirror reduces the amount of light forming the image, but doesn't eliminate half of it.

29. Can you explain why a convex mirror always forms a virtual image?

A convex mirror always forms a virtual image because its reflecting surface curves outward, causing incident light rays to diverge after reflection. These diverging rays never meet to form a real image. Instead, when traced backwards, they appear to originate from a point behind the mirror, creating a virtual image that is always upright and smaller than the object.

30. How does the image in a spherical mirror change if the mirror's surface is not perfectly smooth?

If a spherical mirror's surface is not perfectly smooth, the quality of the image deteriorates. Imperfections cause light to scatter in various directions instead of reflecting in a predictable manner. This results in a blurred or distorted image. The effect is similar to looking at a reflection in rippled water - the basic shape is visible, but details are lost and the image appears fuzzy or wavy.

31. Can you explain why the image distance becomes negative for virtual images in the mirror formula?

The image distance becomes negative for virtual images in the mirror formula to maintain consistency with the sign convention and the physical reality. Virtual images form behind the mirror where light rays don't actually go, but appear to originate from. By convention, we measure distances in the direction of incident light as positive. Since virtual images form in the opposite direction, we assign them negative values to indicate this opposite direction.

32. How does the concept of solid angle relate to image formation in spherical mirrors?

Solid angle is crucial in understanding image formation in spherical mirrors. It represents the angular extent of an object or image as seen from the mirror's center. As an object moves closer to a concave mirror, it subtends a larger solid angle, resulting in a larger image. The relationship between object and image solid angles determines magnification. Understanding solid angles helps explain why closer objects produce larger images and why convex mirrors always produce smaller images.

33. What's the significance of the mirror equation being a reciprocal relationship?

The reciprocal nature of the mirror equation (1/f = 1/u + 1/v) is significant because it simplifies calculations and reveals important optical principles. It shows that object and image distances are inversely related - as one increases, the other decreases. This reciprocal relationship also makes it easy to find the harmonic mean of object and image distances, which equals the focal length. It allows for easy conversion between different units and simplifies the analysis of optical systems.

34. How does astigmatism occur in spherical mirrors, and how does it differ from spherical aberration?

Astigmatism in spherical mirrors occurs when light rays reflecting from different planes of the mirror (e.g., horizontal vs. vertical) focus at different points. This is different from spherical aberration, where rays at different distances from the optical axis focus at different points. Astigmatism is more pronounced for objects off the optical axis and results in images that are focused differently in different planes. While spherical aberration affects the entire image, astigmatism primarily affects off-axis points.

35. Why can't you use the thin lens approximation for thick mirrors?

The thin lens approximation, which assumes all refraction or reflection occurs at a single plane, can't be used for thick mirrors because it doesn't account for the significant distance between the front and back surfaces of the mirror. In thick mirrors, light rays interact with the mirror over a non-negligible distance, leading to additional optical effects. These include spherical aberration, coma, and astigmatism, which become more pronounced as the mirror thickness increases. For accurate analysis of thick mirrors, more complex optical formulas or ray tracing techniques are required.

36. How does the f-number of a spherical mirror relate to its light-gathering power?

The f-number (f/#) of a spherical mirror is the ratio of its focal length to its diameter. A lower f-number indicates greater light-gathering power. This is because the light-gathering power is proportional to the square of the mirror's diameter, while the f-number is inversely proportional to the diameter. Thus, a mirror with a lower f-number has a larger diameter relative to its focal length, allowing it to collect more light. This is crucial in applications like astronomy, where gathering faint light is important.

37. Can you explain how caustics form in spherical mirrors and their significance?

Caustics in spherical mirrors are bright, curved patterns formed by the concentration of reflected light. They occur when light rays from a point source reflect off the curved surface and converge along a curve rather than at a single point. This is due to the mirror's curvature and is related to spherical aberration. Caustics are significant because they represent areas of high light intensity and can affect image quality. Understanding caustics is important in optical design, particularly for applications requiring precise light control or image formation.

38. How does the concept of wavefront relate to image formation in spherical mirrors?

Wavefronts are surfaces of constant phase in a wave. In spherical mirrors, incident plane wavefronts (from distant objects) are transformed into spherical wavefronts upon reflection. The curvature of these reflected wavefronts determines where the image forms. A converging wavefront forms a real image, while a diverging wavefront forms a virtual image. The mirror's shape alters the wavefront curvature, directly affecting image formation. Understanding wavefronts helps explain phenomena like spherical aberration and the limitations of image quality in spherical mirrors.

39. Why do concave mirrors form real images for distant objects but virtual images for close objects?

Concave mirrors form real images for distant objects because parallel light rays from these objects converge to a point after reflection, creating a real image. For close objects (closer than the focal point), the reflected rays diverge and never meet. However, when these diverging rays are traced backwards, they appear to originate from a point behind the mirror, creating a virtual image. This transition occurs at the focal point, where incoming rays become parallel after reflection, forming no image.

40. How does the radius of curvature of a spherical mirror affect its magnification capabilities?

The radius of curvature of a spherical mirror directly affects its magnification capabilities. A smaller radius of curvature (more curved mirror) has a shorter focal length, which can produce higher magnification for objects close to the focal point. However, it also increases aberrations. A larger radius of curvature (flatter mirror) has a longer focal length, producing lower magnification but with fewer aberrations. The magnification also depends on object distance, so the effect of radius of curvature on magnification varies with object position.

41. Can you explain the concept of conjugate points in the context of spherical mirrors?

Conjugate points in spherical mirrors are pairs of points where one point is the object location and the other is its corresponding image location. If light rays from one point converge at the other after reflection, these points are conjugates. The relationship between conjugate points is reciprocal - if the object is placed at the image point, the image will form at the original object point. This concept is fundamental to understanding image formation and is directly related to the mirror equation.

42. How does the principle of reversibility of light apply to spherical mirrors?

The principle of reversibility of light states that light can travel along the same path in either direction. In spherical mirrors, this means that if an object at point A forms an image at point B, then an object at point B will form an image at point A. This principle underlies the reciprocal nature of conjugate points and helps explain why the mirror equation works regardless of which point is considered the object and which is the image.

43. What is the significance of the Gaussian optics approximation in the context of spherical mirrors?

The Gaussian optics approximation, also known as paraxial approximation, assumes that all light rays are close to and make small angles with the optical axis. This simplification allows the use of the simple mirror equation and linear magnification formula. It's significant because it makes calculations much easier and is accurate for many practical situations. However, it breaks down for wide-angle systems or when high precision is required, as it doesn't account for aberrations like spherical aberration or coma.

44. How does the concept of optical power apply to spherical mirrors?

Optical power, measured in diop