Static Friction - Definition, Laws, FAQs
Static friction is the force that resists the initiation of motion between two surfaces in contact. Unlike kinetic friction, which acts when objects are already moving, static friction is what keeps an object at rest despite the presence of an external force. It plays a crucial role in everyday life, from preventing your car from sliding on a hill to ensuring that a book stays put on a slanted desk. Understanding static friction is essential in fields like engineering and physics, where the ability to predict and control motion is key to designing safe and efficient systems. For instance, when you push a heavy piece of furniture, the resistance you initially feel is due to static friction, and only once this force is overcome does the object begin to move.
This Story also Contains
- Static friction
- Solved Example Based on Static Friction
- Conclusion
Static friction is the opposing force that is set up between the surfaces of contact of the two bodies when one body tends to slide over the surface of another body.
Static friction
It occurs when there is a tendency of relative motion, i.e., the body is still at rest and is just about to move.
When two bodies do not slip over each other, then the force of friction is called static friction.
It is a variable force or self-adjusting force as it changes itself according to the applied force.
It is denoted by fs and the static friction is in between:- 0<fs<fl
where fl is limiting friction.
5. Limiting friction is the maximum static friction that a body can exert on the other body in contact with
It is given by
FlαR or fl=μsR
fl= limiting friction μs= coefficient of friction R= reaction force
6. Generally,
fK<Fl∴μK<μs
Recommended Topic Video
Solved Example Based on Static Friction
Example 1: Given in the figure are two blocks A and B of weight 20 N and 100 N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force (in N) applied by the wall on block B is :
1) 120
2) 80
3) 100
4) 150
Solution :
Given :
Weights of blocs A=20 N
Weight of block B=100 N
As the blocks are at rest, both blocks must be in equilibrium.
Let the Friction force between the blocks be f1 and between block B and wall be f2
F.B.D of the blocks :
From F.B.D
F=Nf1=20f2=f1+100⇒f2=20+100=120N
Example 2. A block rests on a rough inclined plane making an angle of 30o with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10 N, the mass of the block (in kg) is (take g = 10 m/s2 )
1) 2.0
2) 4.0
3) 1.6
4) 2.5
Solution
Static Friction
Self-adjusting force because it changes itself according to the applied force.
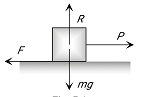
wherein
It is always equal to a net external force. Static friction (F = P) using diag.
For equilibrium of block,
f=mgsinΘ∴10=m×10×sin30∘ or m=2 kg
Hence, the correct option is 1.
Qu 3. An automobile, travelling at 40 km/h, can be stopped at a distance of 40 m by applying brakes. If the same automobile is travelling at 80 km/h, the minimum stopping distance in metres is (assume no skidding) :
1) 160
2) 100
3) 150
4) 75
Solution
Limiting Friction
The magnitude of limiting friction between any two bodies in contact is directly proportional to the normal reaction between them.
FlαR or fl=μsRfl= limiting friction μs= coefficient of friction R= reaction force
The maximum value of static friction is limiting friction.
a=μgs=u22a=u22μgsαu2s2s1=(u2u1)2=(8040)2=4s2=160m(∵s1=40m)
Hence, the answer is 160.
Example 4. A disc rotates about its axis of symmetry in a horizontal plane at a steady rate of 3.5 revolutions per second. A coin placed at a distance of 1.25 cm from the axis of rotation remains at rest on the disc. The coefficient of friction between the coin and the disc is: (g=10 m/s2)
1) 0.6
2) 0.3
3) 0.7
4) 0.5
Solution
Limiting Friction
The magnitude of limiting friction between any two bodies in contact is directly proportional to the normal reaction between them.
FlαR or fl=μsRfl= limiting friction μs= coefficient of friction R= reaction force
wherein
* The maximum value of static friction is limiting friction.
* Direction is always opposite to relative motion.
In equilibrium,
mω2r=μmgμ=ω2rg(ν=3.5rev/sec)ω=2Πv=7Πrad/s=7∗227=22rad/sr=1.25 cm;g=10μ=222∗1.25∗10−210=0.6
Qu 5. A block of mass 4 kg, kept on a rough surface is being pulled by applying a horizontal force of 5N, as shown in the figure. The coefficient of static friction between the block and the surface is 0.2. The friction force acting on the block is-
1) 8N
2) 5N
3) 2N
4) 10N
Solution:
Given
mass of the block, m=4 kg,
Coefficient of the static friction, μs=0.2
Driving force on the block, F=5 N
Let the friction force on the block be f as shown in the diagram
From F.B.D
N=mg
Limiting friction-
fl=μsNfl=μsmgfl=0.2×4×10=8N⇒F<fl
As the applied driving force on the block is less than the limiting friction the block will remain at rest. In such cases static friction acts of magnitude equal to the applied force.
⇒f=F=5N
Conclusion
The maximum value of the force of friction which comes into play before a body just begins to slide over the surface of another body is called the limiting value of static friction.
Frequently Asked Questions (FAQs)