The Dipole In A Uniform Magnetic Field

A dipole in a uniform magnetic field refers to a system where a magnetic dipole, typically modelled as a small bar magnet or current loop, is placed in a region where the magnetic field strength is constant. The interaction between the dipole's magnetic moment and the external magnetic field leads to a torque that tends to align the dipole with the field. This phenomenon can be observed in various real-life scenarios, such as in compasses, where the Earth's magnetic field aligns the needle, and in MRI machines, where the behaviour of atomic nuclei in magnetic fields helps create detailed images of the human body. The study of dipoles in uniform magnetic fields is critical in understanding electromagnetism and has wide applications in modern technologies, from electric motors to magnetic storage devices.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. The Dipole in a Uniform Magnetic Field
2. Net Force
3. Solved Examples Based on The Dipole In a Uniform Magnetic Field
4. Summary

The Dipole in a Uniform Magnetic Field

A dipole in a uniform magnetic field refers to a magnetic system consisting of two equal and opposite magnetic poles or a current loop placed in a region where the magnetic field strength is constant. When such a dipole is introduced into this field, it experiences a torque that tends to align the dipole's magnetic moment with the direction of the field. This alignment is similar to how a compass needle aligns itself with the Earth's magnetic field, which is a natural dipole in a relatively uniform magnetic field.

Net Force

A magnetic dipole is analogous to an electric dipole.

So we can use $m=q_m$
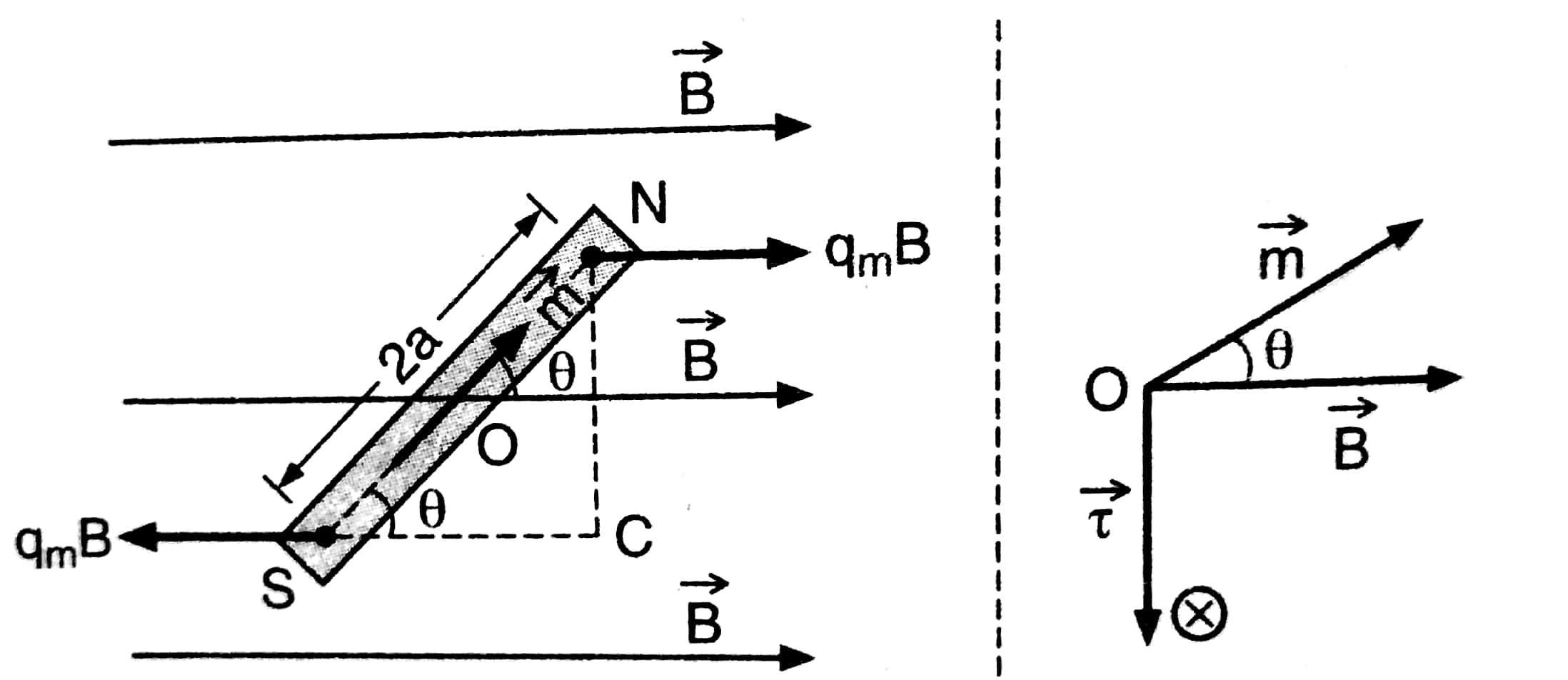
when a magnetic dipole is kept in a uniform magnetic field. The net force experienced by the dipole is zero as shown in the below figure.
I.e $F_{n e t}=0$

Hence magnetic dipole will not make any linear motion.

Torque on Dipole

Net torque about the center of dipole is given as $\tau=q_m B(2 a) \sin \theta$
Using $\vec{M}=q_m 2 a_{\text {we get }} \tau=M B \sin \theta$
So $\vec{\tau}=\vec{M} \times \vec{B}$
- The direction of the torque is normal to the plane containing dipole moment M and magnetic field B and is governed by the right-hand screw rule.
- If Dipole is parallel to B the torque is Zero. I.e $\theta=0^{\circ} \quad \tau=0$ (This is the position of stable equilibrium of dipole)
- Torque is maximum when Dipole is perpendicular to B. I.e
$\theta=\frac{\pi}{2}$
$\tau=M B=$ maximum torque

Oscillation of Dipole

If a dipole experiencing a torque in a magnetic field is allowed to rotate, then it will rotate to align itself to the magnetic field. But when it reaches along the direction of B the torque becomes zero. However, due to inertia, it overshoots this equilibrium condition and then starts oscillating about this mean position.

The time period of this oscillation is given as

$T=2 \pi \sqrt{\frac{I}{M B}}$

where I= moment of inertia of dipole about the axis passing through its centre and perpendicular to its length.

• For two magnets having Magnetic Moments in the same direction (i.e sum position of the magnetic moment)

$
\begin{aligned}
& M_s=M_1+M_2 \\
& I_s=I_1+I_2
\end{aligned}
$

$M_s$ - Net Magnetic Moment
$I_s$ - Net Moment of Inertia
So Time period is

$
T=2 \pi \sqrt{\frac{I_s}{M_s B}}
$
Similarly, Frequency is given as

$
\nu=\frac{I}{T_s}=\frac{1}{2 \pi} \sqrt{\frac{\left(M_1+M_2\right) B}{I_s}}
$

• For two magnets having Magnetic Moments in the opposite direction (i.e different positions of the magnetic moment)

$
\begin{aligned}
& M_d=M_1-M_2 \\
& I_d=I_1+I_2
\end{aligned}
$
So Time period is

$
T=2 \pi \sqrt{\frac{I_d}{M_d B}} \text { or } \quad T_d=2 \pi \sqrt{\frac{I_1+I_2}{\left(M_1-M_2\right) B}}
$
Similarly, Frequency is given as

$
\nu_d=\frac{1}{T_d}=\frac{1}{2 \pi} \sqrt{\frac{\left(M_1-M_2\right) B}{I_1+I_2}}
$

• The ratio of difference and sum position of the magnetic moment

$\begin{aligned} & \frac{T_s}{T_d}=\sqrt{\frac{M_1-M_2}{M_1+M_2}} \\ & \frac{M_1}{M_2}=\frac{T_d^2+T_s^2}{T_d^2-T_s^2}=\frac{\nu_s^2+\nu_d^2}{\nu_s^2-\nu_d^2}\end{aligned}$

Dipole in Non-Uniform Magnetic Field

In case the magnetic field is non-uniform, the magnitude of the force on $+q_m$ and $-q_m$ will be different. $\left.\underline{S o} F_{\text {( }} n e t\right) \neq 0$ and At the same time due to a couple of forces acting, a torque will also be acting on it.

Work done in Rotation

Then work done by magnetic force for rotating a magnetic dipole through an angle $\theta_2$ from the equilibrium position of an angle $\theta_1$ (As shown in the above figure) is given as

$
\begin{aligned}
& W_{m a g}=\int \tau d \theta=\int_{\theta_1}^{\theta_2} \tau d \theta \cos \left(180^0\right)=-\int_{\theta_1}^{\theta_2} \tau d \theta \\
& \Rightarrow W_{m a g}=-\int_{\theta_1}^{\theta_2}(M \times B) d \theta=-\int_{\theta_1}^{\theta_2}(M B \operatorname{Sin} \theta) d \theta=M B\left(\cos \theta_2-\cos \theta_1\right)
\end{aligned}
$
And So work done by an external force is $W=-W_{\operatorname{mag}}=M B\left(\cos \theta_1-\cos \theta_2\right)$
For example

$
\begin{gathered}
\text { if } \theta_1=0^{\circ} \text { and } \theta_2=\theta \\
W=M B(1-\cos \theta) \\
\text { if } \theta_1=90^{\circ} \text { and } \theta_2=\theta \\
W=-M B \cos \theta
\end{gathered}
$

Potential Energy of a Dipole Kept in a Magnetic Field

As $\Delta U=-W_{m a g}=W$

So change in Potential Energy of a dipole when it is rotated through an angle $\theta_2$ from the equilibrium position of an angle $\theta_1$ is given as $\Delta U=M B\left(\cos \theta_1-\cos \theta_2\right)$

$
\begin{aligned}
& \text { if } \theta_1=90^{\circ} \text { and } \theta_2=\theta \\
& \Delta U=U_{\theta_2}-U_{\theta_1}=U_\theta-U_{90}=-M B \cos \theta
\end{aligned}
$
Assuming $\theta_1=90^{\circ}$ and $U_{90^{\circ}}=0$
we can write $U=U_\theta=-\vec{M} \cdot \vec{B}$

Equilibrium of Dipole

1. Stable Equilibrium

$
\begin{aligned}
& \theta=0^{\circ} \\
& \tau=0 \\
& U_{\min }=-M B
\end{aligned}
$

2. Unstable Equilibrium

$
\begin{aligned}
& \theta=180^{\circ} \\
& \tau=0 \\
& U_{\max }=M B
\end{aligned}
$

3. Not in equilibrium

$
\begin{aligned}
& \theta=90^{\circ} \\
& \tau_{\max }=M B \\
& U=0
\end{aligned}
$

Recommended Topic Video

Solved Examples Based on The Dipole In a Uniform Magnetic Field

Example 1: A magnetic needle lying parallel to a magnetic field requires W units of work to turn it through 60⁰ . The torque needed to maintain the needle in this position will be

1) $\sqrt{3} \mathrm{~W}$
2) W
3) $\left(\frac{\sqrt{3}}{2}\right) W$
4) 2 W

Solution:

Torque

$\begin{aligned} \vec{\tau} & =\vec{M} \times \vec{B} \\ \tau & =M B \sin \theta\end{aligned}$

wherein

and

Work done by bar magnet
$
\begin{aligned}
& W=M B(1-\cos \theta) \\
& W=-M B\left(\cos \theta_2-\cos \theta_1\right) \\
& =-M B\left(\cos 60^{\circ}-\cos 0\right)=\frac{M B}{2} \\
& \therefore M B=2 W \ldots \ldots \ldots(i) \\
& \text { Torque }=M B \sin 60^{\circ}=(2 W) \sin 60^0 \\
& =\frac{2 W \times \sqrt{3}}{2}=\sqrt{3} W
\end{aligned}
$

Hence, the answer is the option (1).

Example 2: A short bar magnet of magnetic moment 0.4JT^-1 is placed with a uniform magnetic field of 0.16T. The magnet is in stable equilibrium when the potential energy (in J) is :

1) -0.064

2) 0.064

3) -0.082

4) 0

Solution:

Potential Energy
$
U=-M B \cos \theta=-\vec{M} \cdot \vec{B}
$

wherein
$\theta$ - angle made by the dipole with the field
For stable equilibrium

$
\begin{aligned}
& U=-M B \\
& =-(0.4)(0.16)=-0.064 \mathrm{~J}
\end{aligned}
$

Hence, the answer is the option (2).

Example 3: Keeping dissimilar poles of two magnets of equal pole strength and length same side, their time period will be

1) Zero

2) one second

3) Infinity

4) Any value

Solution:

Magnetic Moments of two magnets
$
\begin{aligned}
& M_s=M_1-M_2 \\
& I_s=I_1+I_2
\end{aligned}
$

$M_s$ - Net Magnetic Moment
$I_s$ - Net Moment of Inertia
wherein

$
T=2 \pi \sqrt{\frac{I_1+I_2}{\left(M_1-M_2\right) B_H}}
$
Here, $M_1=M_2$

$
\therefore T=\infty
$

Hence, the answer is the option (3).

Example 4: A bar magnet A of magnetic moment M_A is found to oscillate at a frequency twice that of magnet B of magnetic moment M_B when placed in a vibrating magnetometer. we say that

1) $M_A=2 M_B$
2) $M_A=8 M_B$
3) $M_A=4 M_B$
4) $M_A=8 M_B$

Solution:
$
\begin{aligned}
& v=\frac{1}{2 \pi} \sqrt{\frac{M B_H}{I}} \Rightarrow v \propto \sqrt{M} \\
& \Rightarrow \frac{v_A}{v_B}=\sqrt{\frac{M_A}{M_B}} \Rightarrow \frac{2}{1}=\sqrt{\frac{M_A}{M_B}} \Rightarrow M_A=4 M_B
\end{aligned}
$

Hence, the answer is the option (3).

Example 5: In sum and difference method in vibration magnetometer, the time period is more if:

1) Similar poles of both magnets are on the same side

2) Opposite poles of both magnets are on the same side

3) Both magnets are perpendicular to each other

4) Nothing can be said

Solution:

In sum position $\mathrm{Ts}=2 \pi \sqrt{\frac{I_s}{\left(M_1+M_2\right) B_H}}$
In difference position: $\mathrm{Td}=2 \pi \sqrt{\frac{I_d}{\left(M_1-M_2\right) B_H}}$
It is clear that $\mathrm{Td}>\mathrm{Ts}$.

Hence, the time period is more, if the opposite poles of both magnets are on the same side.

Hence, the answer is the option (2).

Summary

A magnetic dipole in a uniform magnetic field experiences torque, aligning it with the field direction but without linear motion. The torque depends on the dipole's orientation, reaching zero when aligned and maximum when perpendicular to the field. In non-uniform fields, a net force and torque act on the dipole. The potential energy and equilibrium of the dipole vary with its angle relative to the field, influencing its stability. These principles are crucial in understanding the behaviour of magnetic systems and their applications in real-world technologies like MRI and electric motors.