Thermal Conductivity Unit - Definition, Formula, FAQs

Edited By Vishal kumar | Updated on Jul 02, 2025 04:58 PM IST

Key points of this article

Thermal conductivity
Unit and dimension of thermal conductivity
Thermal resistance
Coefficient of thermal conductivity

Thermal conductivity:- It is the capacity of a material to conduct the heat. Thermal conductivity is denoted by K which is known as the coefficient of thermal conductivity.

Also read -

What is the coefficient of thermal conductivity?

Let’s discuss, Suppose a parallel-faced slab. The cross-sectional area is A and length l of this slab. The temperatures of the faces are at a steady temperature ?1 and ?2. Heat will flow through the face at a higher temperature ?1 to that at a lower temperature ?2. Let us assume that there is no heat that comes out from the edges of the slab. Thus, the line of the flow will be normal at all points of the faces of the slab. In these situations, under steady-state, the quantity of heat Q entering one face at a given time is the same as the heat leaving the other face at the same time.

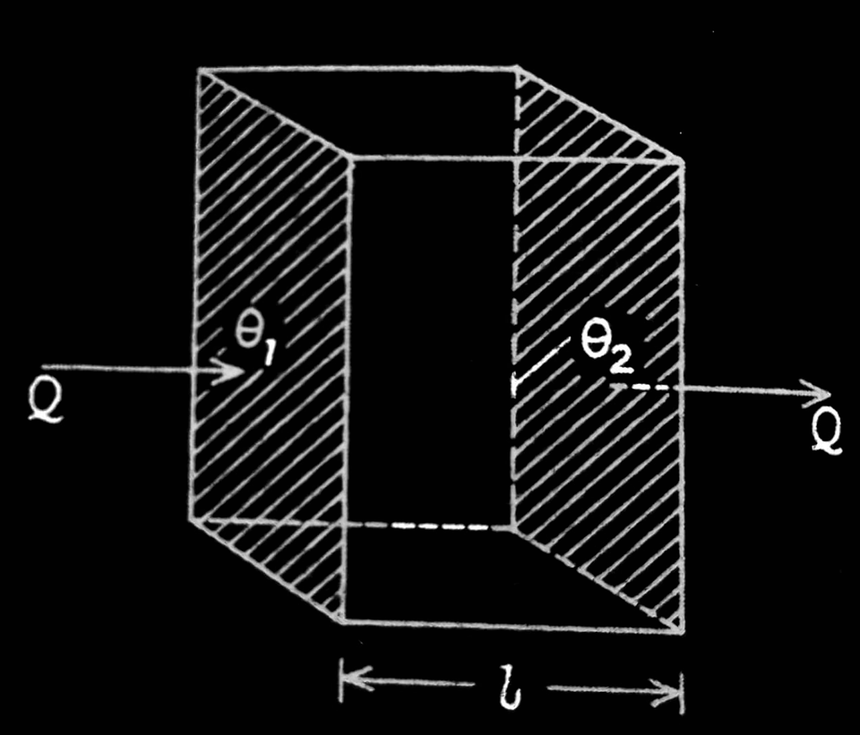
Thermal Conductivity Unit - Definition, Formula, FAQs

Thermal conductivity

The test shows that the heat Q is

(i) directly proportional to the cross-sectional area A of each face,

Q ∝ A …..1

(ii) directly proportional to the temperature difference (?1 -?2 ) between two faces,

Q ∝ (?₁ - ?₂ ) …...2

(iii) directly proportional to the time t . ( time for which the heat flows in the slab),

Q ∝ t …..3

(iv) inversely proportional to the length of the slab (distance between hot and cold faces),

Q ∝ 1/l …..4

From eqn 1, 2, 3, and 4 we have

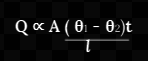
thermal conductivity

Where k is a constant which depends upon the material. It is called the coefficient of thermal conductivity. The quantity (?₁- ?₂ )/l is the “temperature gradient” across the slab. It is a measure of the change in temperature with distance. SI unit of temperature gradient is Kelvin/meter.

If A = 1, (?₁- ?₂ )/l = 1 and t = 1, then K = Q. Therefore, the coefficient of thermal conductivity K of a material is defined as the amount of heat that flows in unit time through the unit area of the material perpendicular to the flow under unit- temperature gradient, when the steady-state has been reached.

If K is large for material then it is a good heat conductor, whereas If K is small for material then it is a poor conductor of heat. For an ideal or perfect heat conductor, K will be infinite, and for a perfect heat insulator, the value of K is zero.

In case when the heat escapes out from the sides of the slab, the temperature gradient is not uniform across the slab. In such a case, if θ and θ + ?θ be the temperature at a plane distance x and x + ?x along the direction of heat flow, then the temperature gradient will be θ - ( θ + ?θ )/?x = -?θ/?x. In the limit ?x→0; this becomes -dθ/dx which is the temperature gradient at the plane x. ( The negative sign expresses the fact that the temperature always decreases in the direction of heat flow ). Then, the heat dQ flowing across the plane x in time dt will be given by

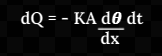
thermal conductivity

The rate of flow of heat is

rate of flow of heat

The unit of thermal conductivity:- We know that

We get,

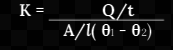
Coefficient of thermal conductivity

Thus, SI unit of coefficient of thermal conductivity is Js-¹m-¹K-¹ or Wm-¹K-¹. CGS unit of coefficient of thermal conductivity K is expressed in cal.s-¹cm-¹°C-¹

Related Topics Link,

Thermal conductivity also has the dimensional formula. So, what is the dimensional formula of thermal conductivity?

Dimensional formula of thermal conductivity:- Coefficient of thermal conductivity dimensional formula is [MLT-¹?-¹].

The ratio of the coefficient of thermal conductivity of two different materials is 5:3. If the thermal resistance of the rod of the same thickness resistance of the rods of the same thickness of these materials is the same, then the ratio of the length of these rods will be

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Solution:- Let the coefficient of thermal conductivity of two different materials is represented by K1 and K2.

So, K₁/K₂ = 5/3

Given, the thermal resistance of rods is the same R1 = R2

We know that R = l/KA

∴ A₁ = A₂ = A

R₁ = R₂

l₁/K₁A = l₂/K₂A

l₁/5 = l₂/3

l₁/l₂ = 5/3

So, the ratio of the length of these rods 5:3

Also Read:

Thermal resistance:- Just as charge flows in an electrical circuit due to a potential difference between two points of the circuit, in the same way, heat flows in a conductor due to a temperature difference between two conductors (or b/w two points of the conductor). Hence, like electrical resistance, there is also thermal resistance in a material.

Let l be the length and A be the area of cross-section of a rod. Let θ1 and θ2 be the temperatures of the hot and cold ends of the rod in the steady-state. The rate of flow of heat is given by

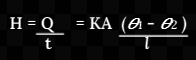
1640876712547

When a current flows in a conductor, the ratio V/i is called the electric resistance R of the conductor, where V is the potential difference between the ends of the conductor and i is the current and rate of flow of charge in a conductor. In the above formula (θ1 - θ2 ) is the temperature difference between the ends of the conductor and H is the rate of flow of heat. On this basis, (θ1 - θ2 )/H is called the thermal resistance R of the conductor. Thus,

From the above equation, If the coefficient of thermal conductivity of a material is greater, the smaller is the thermal resistance of a rod of that material.

SI unit of thermal resistance:- The unit of thermal resistance is second°C/kilo-calorie.

Dimensional formula of thermal resistance:- The dimensional formula of thermal resistance is [M-¹L-²T³?].

Thermal conductance:- It is the ability of a material to measure the heat transfer per unit time. The thermal conductance unit or conduction unit is W⋅K⁻¹

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. Write the dimensional formula of conductivity

Dimension of coefficient of thermal conductivity or dimension of conductivity is [MLT-¹?-¹].

2. What is the unit of thermal conductivity? Or what is the SI unit of thermal conductivity?

Unit of thermal conductivity is ( or unit of coefficient of thermal conductivity) SI unit of thermal conductivity is Js-¹m-¹K-¹ or Wm-¹K-¹.

3. Write the formula of coefficient of thermal conductivity

The formula of coefficient of thermal conductivity is

Q = KA. (θ1 - θ2 )t/l

So, K = (Q/t)/(A/l).(θ1 - θ2 )

Where K is the coefficient of thermal conductivity.

4. Define thermal conductivity and its si unit

Thermal conductivity or the coefficient of thermal conductivity K of a material is defined as the amount of heat that flows in unit time through the unit area of the material perpendicular to the flow under unit- temperature gradient when the steady-state has been reached.

The unit of thermal conductivity is Js-¹m-¹K-¹ or Wm-¹K-¹.

5. Write about the thermal resistance and its SI unit.

The thermal resistance is the ratio of length of the rod of the material and the product of the coefficient of thermal conductivity and the area of cross-section of the rod.

R = l/KA

Where, l= length of rod

K = thermal conductivity

A = area of cross-section.

If the resistance increases thermal conductivity decreases and vice versa.

The SI unit of thermal resistance is second°C/kilo-calorie.

6. What is thermal conductivity?

Thermal conductivity is a measure of a material's ability to conduct or transfer heat. It quantifies how easily heat flows through a substance when there is a temperature difference across it. Materials with high thermal conductivity allow heat to pass through them quickly, while those with low thermal conductivity are good insulators.

7. What is the unit of thermal conductivity?

The SI unit of thermal conductivity is watts per meter-kelvin (W/m·K). This unit represents the amount of heat (in watts) that flows through a material of 1 meter thickness when there is a temperature difference of 1 kelvin across it.

8. Can thermal conductivity be negative?

No, thermal conductivity cannot be negative. It is always a positive value because heat naturally flows from higher temperature regions to lower temperature regions. A negative thermal conductivity would imply heat flowing from cold to hot, which violates the second law of thermodynamics.

9. What is the formula for thermal conductivity?

The formula for thermal conductivity (k) is:

10. How is thermal conductivity different from heat conduction?

Thermal conductivity is a property of a material, while heat conduction is the process of heat transfer. Thermal conductivity measures how well a material conducts heat, whereas heat conduction refers to the actual transfer of thermal energy from one particle to another within a substance due to a temperature gradient.

11. Why do metals generally have higher thermal conductivity than non-metals?

Metals generally have higher thermal conductivity because they have free electrons that can move easily throughout the material. These electrons can quickly transfer kinetic energy (heat) from one atom to another, allowing for efficient heat conduction. Non-metals lack these free electrons, resulting in lower thermal conductivity.

12. What is the relationship between electrical conductivity and thermal conductivity?

There is often a correlation between electrical and thermal conductivity, especially in metals. This relationship is described by the Wiedemann-Franz law, which states that the ratio of thermal conductivity to electrical conductivity is proportional to temperature. Materials that are good electrical conductors are usually good thermal conductors as well.

13. What is the Kapitza resistance and how does it relate to thermal conductivity?

Kapitza resistance, also known as thermal boundary resistance, is the resistance to heat flow that occurs at the interface between two materials. It's particularly important in nanoscale heat transfer. While thermal conductivity describes heat flow within a material, Kapitza resistance affects heat transfer across material boundaries, which can significantly impact overall thermal performance in composite systems or nanostructures.

14. How does thermal conductivity affect the cooking process in different types of cookware?

Thermal conductivity greatly influences cooking performance. Cookware made of materials with high thermal conductivity, like copper or aluminum, heats up quickly and distributes heat evenly, allowing for precise temperature control. Materials with lower thermal conductivity, like stainless steel, heat more slowly and may have hot spots, but they retain heat well. The choice of cookware material affects cooking time, energy efficiency, and food quality.

15. What is the relationship between thermal conductivity and superconductivity?

While thermal conductivity and superconductivity are both related to energy transfer, they behave differently. In normal conductors, thermal and electrical conductivity are often correlated. However, in superconductors, while electrical resistance drops to zero below a critical temperature, thermal conductivity doesn't follow the same pattern. In fact, thermal conductivity in superconductors can be quite low, as the electrons that form Cooper pairs don't contribute significantly to heat transfer.

16. How does thermal conductivity affect the formation of convection currents in fluids?

Thermal conductivity plays a role in initiating convection currents, but convection itself is a different heat transfer mechanism. In fluids with low thermal conductivity, temperature gradients persist longer, which can enhance the formation of convection currents. Conversely, high thermal conductivity can quickly equalize temperatures, potentially reducing the driving force for convection. However, once convection is established, it typically dominates heat transfer in fluids.

17. How does thermal conductivity impact the effectiveness of thermal insulation in spacecraft?

In spacecraft, thermal insulation is crucial for maintaining appropriate temperatures in the extreme conditions of space. Materials with very low thermal conductivity are used to prevent heat loss in cold environments and heat gain in hot environments. Multi-layer insulation (MLI) is often used, consisting of multiple layers of low-emissivity films separated by low-conductivity spacers, effectively combining low thermal conductivity with radiation reflection to achieve superior insulation in the vacuum of space.

18. How does thermal conductivity affect the formation and stability of snowflakes?

Thermal conductivity plays a role in snowflake formation and stability. As water vapor condenses and freezes on a growing snowflake, the latent heat released must be conducted away. The low thermal conductivity of air around the snowflake helps maintain temperature gradients necessary for growth. Within the snowflake, the thermal conductivity of ice affects how quickly heat is distributed, influencing the growth pattern and ultimately the snowflake's shape and stability.

19. How does thermal conductivity affect the efficiency of thermoelectric devices?

In thermoelectric devices, which convert temperature differences directly into electricity (or vice versa), thermal conductivity plays a crucial role. For high efficiency, materials should have high electrical conductivity but low thermal conductivity. This combination allows for maintaining a large temperature gradient while efficiently conducting electricity. The figure of merit ZT, which determines thermoelectric efficiency, is inversely proportional to thermal conductivity. Therefore, reducing thermal conductivity without significantly affecting electrical conductivity is a key goal in thermoelectric material research.

20. What is the concept of ballistic thermal conduction and when does it become significant?

Ballistic thermal conduction occurs when the characteristic length of a material is smaller than the mean free path of the heat carriers (usually phonons or electrons). In this regime, heat carriers travel through the material without scattering, leading to behavior that deviates from classical thermal conduction described by Fourier's law. This becomes significant in nanostructures or at very low temperatures where the mean free path increases. Ballistic conduction can result in higher effective thermal conductivity than predicted by bulk properties.

21. How does thermal conductivity affect the formation of urban heat islands?

Urban heat islands form partly due to the thermal properties of urban materials. Materials like concrete and asphalt, which are common in cities, have higher thermal conductivity and heat capacity than natural surfaces. They absorb and store heat during the day and release it slowly at night. This, combined with reduced vegetation (which provides cooling through evapotranspiration), leads to higher temperatures in urban areas compared to surrounding rural areas. Understanding thermal conductivity helps in designing urban spaces to mitigate heat island effects.

22. What is the relationship between thermal conductivity and the speed of sound in a material?

There is a relationship between thermal conductivity and the speed of sound in a material, particularly in solids. Both properties depend on the elastic properties and density of the material. In many solids, especially metals, thermal energy is primarily conducted by lattice vibrations (phonons), which are also responsible for sound propagation. Materials with higher speed of sound often have higher thermal conductivity. This relationship is not always direct and can be influenced by other factors, but it provides a useful correlation in many cases.

23. How does thermal conductivity affect the performance of thermal barrier coatings in gas turbines?

Thermal barrier coatings (TBCs) in gas turbines rely on low thermal conductivity to protect underlying metal components from extreme temperatures. The effectiveness of a TBC is largely determined by its ability to maintain a temperature gradient, which is directly related to its thermal conductivity. Materials with very low thermal conductivity are used to maximize the temperature drop across the coating, allowing the engine to operate at higher temperatures for improved efficiency while keeping the metal components within safe temperature limits.

24. What is the concept of minimum thermal conductivity and how is it determined?

Minimum thermal conductivity is a theoretical lower limit for the thermal conductivity of a material. It's based on the idea that heat transfer can't be slower than the propagation of individual atomic vibrations. The concept is particularly relevant for amorphous materials and some crystals at high temperatures. It's typically estimated using models that consider the material as a collection of harmonic oscillators with minimum mean free paths. Understanding minimum thermal conductivity is important in the design of thermal insulators and thermoelectric materials.

25. How does thermal conductivity affect the formation and behavior of thermal plumes in the Earth's mantle?

Thermal conductivity plays a crucial role in mantle convection and the formation of thermal plumes. Regions of the mantle with lower thermal conductivity retain heat better, which can lead to the development of hot, buoyant plumes that rise towards the surface. The contrast in thermal conductivity between the plume and surrounding mantle affects the plume's shape, rise speed, and longevity. Understanding these thermal properties helps geologists model mantle dynamics and explain phenomena like hotspot volcanism.

26. How does thermal conductivity affect the efficiency of cryogenic systems?

In cryogenic systems, which operate at very low temperatures, thermal conductivity plays a crucial role in both insulation and heat transfer. Materials with extremely low thermal conductivity are used for insulation to minimize heat ingress from the environment. Conversely, high thermal conductivity materials are used in cold heads and heat exchangers to efficiently remove heat. The temperature dependence of thermal conductivity becomes particularly important, as many

27. How does thermal conductivity relate to Fourier's Law of Heat Conduction?

Thermal conductivity is a key component in Fourier's Law of Heat Conduction. The law states that the rate of heat transfer through a material is proportional to the negative temperature gradient and the area perpendicular to that gradient. Thermal conductivity is the proportionality constant in this relationship.

28. How does temperature affect thermal conductivity?

For most materials, thermal conductivity changes with temperature. In metals, it typically decreases as temperature increases due to increased atomic vibrations that impede electron movement. In non-metals, it often increases with temperature as higher molecular vibrations facilitate better energy transfer.

29. What is the difference between thermal conductivity and thermal diffusivity?

Thermal conductivity measures a material's ability to conduct heat, while thermal diffusivity measures how quickly a material can change its temperature when heat is applied. Thermal diffusivity is related to thermal conductivity but also takes into account the material's density and specific heat capacity.

30. Can thermal conductivity be measured directly?

Thermal conductivity is typically not measured directly but is calculated from other measurable quantities. Common methods include the guarded hot plate method, heat flow meter method, and transient plane source method, which measure heat flow and temperature differences to determine thermal conductivity.

31. What is the significance of thermal conductivity in building insulation?

Thermal conductivity is crucial in building insulation as it determines how effectively a material can prevent heat transfer. Materials with low thermal conductivity are ideal for insulation because they reduce heat loss in winter and heat gain in summer, improving energy efficiency and comfort in buildings.

32. How does porosity affect thermal conductivity?

Porosity generally decreases thermal conductivity. As the number of pores (air spaces) in a material increases, heat transfer becomes less efficient because air has a lower thermal conductivity than most solids. This is why materials like foam and fiberglass are effective insulators.

33. How does thermal conductivity affect heat sinks in electronic devices?

Heat sinks in electronic devices rely on high thermal conductivity to efficiently dissipate heat. Materials with high thermal conductivity, like aluminum or copper, are used to quickly draw heat away from sensitive components and spread it over a larger surface area for cooling, preventing overheating and improving device performance.

34. What is the thermal conductivity of a vacuum?

The thermal conductivity of a perfect vacuum is zero because there are no particles to transfer heat energy. However, in practice, even in high-quality vacuums, there is still some heat transfer due to radiation. In engineering applications, the effective thermal conductivity of a vacuum is typically very low but not exactly zero.

35. How does thermal conductivity relate to the concept of R-value in insulation?

R-value is inversely related to thermal conductivity. It measures thermal resistance, which is the ability of a material to resist heat flow. Materials with low thermal conductivity have high R-values, making them good insulators. The R-value is calculated by dividing the thickness of the material by its thermal conductivity.

36. Can thermal conductivity be anisotropic?

Yes, thermal conductivity can be anisotropic, meaning it varies depending on the direction of heat flow within the material. This is common in materials with a layered or fibrous structure, such as wood or certain composites, where heat may flow more easily along the grain or fibers than across them.

37. What is the difference between thermal conductivity and thermal conductance?

Thermal conductivity is a material property independent of size or shape, while thermal conductance is the heat transfer rate through a specific object or structure. Conductance depends on the material's thermal conductivity, as well as its thickness and surface area. Conductance is expressed in watts per kelvin (W/K).

38. How does the atomic structure of a material influence its thermal conductivity?

The atomic structure greatly influences thermal conductivity. Materials with strong interatomic bonds and regular crystal structures (like diamond) tend to have higher thermal conductivity. In contrast, materials with weak bonds or disordered structures (like glasses) typically have lower thermal conductivity due to increased phonon scattering.

39. What role does thermal conductivity play in the formation of frost on surfaces?

Thermal conductivity affects frost formation by influencing how quickly heat is transferred from a surface to the surrounding cold air. Materials with high thermal conductivity, like metals, can rapidly conduct heat away from their surface, reaching the dew point temperature more quickly and facilitating frost formation faster than materials with low thermal conductivity.

40. How does thermal conductivity impact the efficiency of thermal energy storage systems?

In thermal energy storage systems, materials with high thermal conductivity can quickly absorb or release heat, allowing for rapid charging and discharging. However, they may also lose heat more quickly during storage. Low thermal conductivity materials retain heat better but take longer to charge and discharge. The choice depends on the specific application and desired performance characteristics.

41. How do phase changes affect thermal conductivity?

Phase changes can significantly alter thermal conductivity. For example, when a solid melts into a liquid, its thermal conductivity usually decreases due to the increased molecular motion and reduced structural order. Similarly, the transition from liquid to gas typically results in a further decrease in thermal conductivity due to the increased spacing between molecules.

42. What is the concept of effective thermal conductivity in composite materials?

Effective thermal conductivity is a term used for heterogeneous or composite materials that combines the thermal conductivities of its components. It represents the overall heat transfer capability of the composite as if it were a homogeneous material. The effective thermal conductivity depends on the thermal conductivities of the individual components, their volume fractions, and their spatial arrangement within the composite.

43. What is the significance of the thermal conductivity ratio in heat exchangers?

The thermal conductivity ratio in heat exchangers refers to the relative thermal conductivities of the fluids and the exchanger material. A high ratio between the exchanger material and the fluids is desirable as it promotes efficient heat transfer. This ratio affects the overall heat transfer coefficient and, consequently, the size and efficiency of the heat exchanger. Designers must consider this ratio when selecting materials and optimizing heat exchanger performance.

44. What is the concept of phonon mean free path and how does it relate to thermal conductivity?

The phonon mean free path is the average distance a phonon (a quantum of vibrational energy) travels before colliding with another phonon or impurity. It's directly related to thermal conductivity: materials with longer phonon mean free paths generally have higher thermal conductivity. Factors that reduce the mean free path, such as impurities, defects, or boundaries, typically lower thermal conductivity. This concept is particularly important in understanding heat transfer in nanostructures and designing thermoelectric materials.

45. What is the Wiedemann-Franz law and how does it relate thermal and electrical conductivity?

The Wiedemann-Franz law states that the ratio of thermal conductivity to electrical conductivity in metals is proportional to temperature. Mathematically, it's expressed as k/σ = LT, where k is thermal conductivity, σ is electrical conductivity, T is absolute temperature, and L is the Lorenz number. This law highlights that in metals, free electrons are responsible for both heat and electrical conduction. It's particularly useful in estimating one conductivity when the other is known.

46. What is the significance of thermal conductivity in the design of heat shields for atmospheric reentry?

In heat shields for atmospheric reentry, thermal conductivity is a critical property. The ideal heat shield material has low thermal conductivity to prevent heat from reaching the spacecraft's interior. However, it must also be able to withstand extremely high temperatures and ablate (wear away) in a controlled manner to carry away heat. The balance between thermal conductivity, heat capacity, and ablation rate determines the effectiveness of the heat shield in protecting the spacecraft during the intense heating of reentry.