Toroid

A toroid is a fascinating geometric shape that is widely used in physics and engineering, particularly in the study of electromagnetism. Essentially, a toroid is a doughnut-shaped coil of wire, with a hollow center, where the wire is wound in a circular loop. This structure creates a magnetic field confined within the loop, making it highly efficient for certain applications. In real life, toroids are found in a variety of devices, from transformers and inductors in electronic circuits to the magnetic confinement systems in fusion reactors. The design of a toroid is particularly advantageous because it reduces electromagnetic interference, making it ideal for sensitive electronic equipment. The way a toroid confines magnetic fields can be likened to how a road guides traffic, channelling energy in a controlled and efficient manner.

This Story also Contains

1. Toroid
2. Solved Examples Based on Toroid
3. Summary

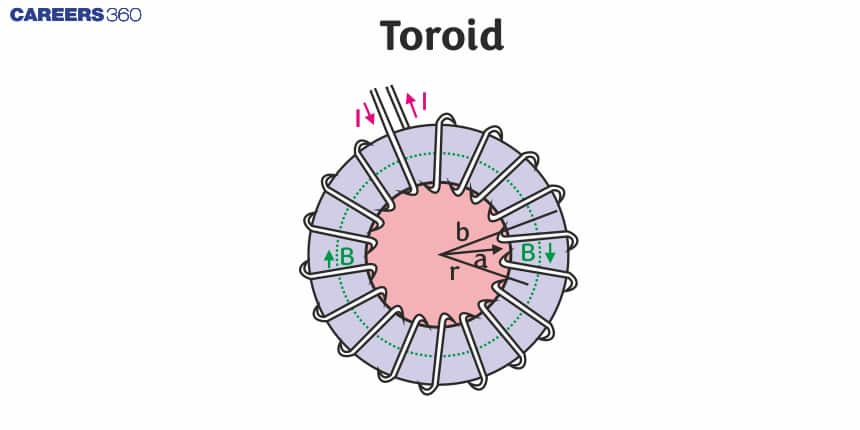
Toroid

A toroid is a distinct and intriguing geometric shape that plays a significant role in physics, particularly in the field of electromagnetism. It is essentially a hollow ring or doughnut-shaped object formed by winding a long coil of wire into a circular loop. When an electric current flows through the wire, it generates a magnetic field that is largely confined within the core of the toroid, making it an ideal component for various applications.

If we try to bend a solenoid in the form of a ring then the obtained shape is a Toroid. So, a toroid can be considered a ring-shaped closed solenoid. Hence it is like an endless cylindrical solenoid. From the given figure we can understand Toroid much better.

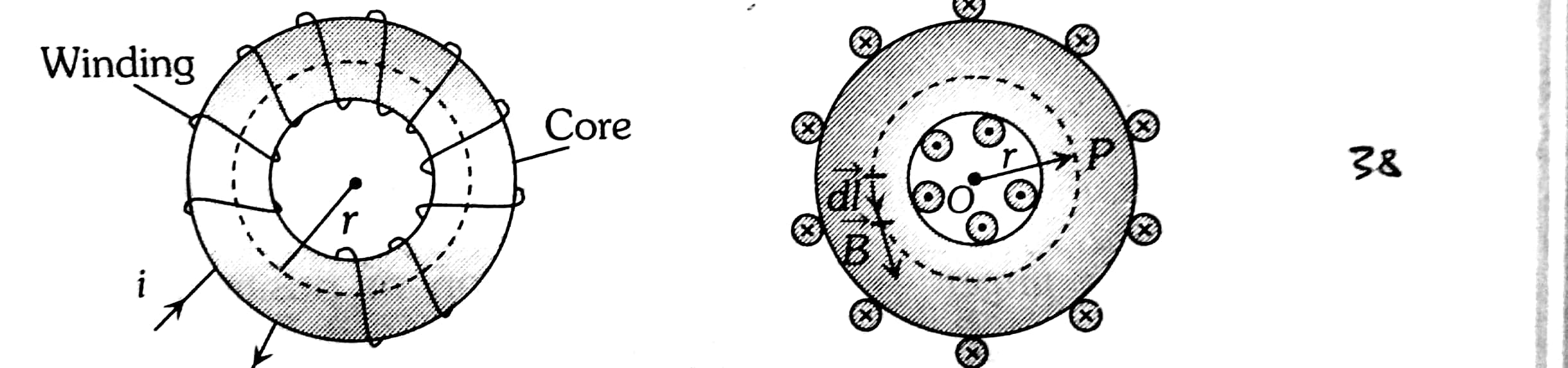
Now to obtain the magnetic field by a toroid, let us consider a toroid having N turns.

Here, we will now apply the Ampere circuital law to calculate the magnetic field of a toroid. Suppose we have to find the magnetic field B at a point P inside the toroid as shown below in Figure -

Let us take an amperian loop which is a circle through point P and concentric inside the toroid. By symmetry, the field will have equal magnitude at all points of this circle and this field is tangential to every point in the circle
Thus,

$
\oint B \cdot d l=\mu_0 \mathrm{NI}
$
or,
$
2 \pi r \mathrm{~B}=\mu_0 \mathrm{NI}
$
or,
$
\mathrm{B}=\frac{\mu_0 \mathrm{NI}}{2 \pi r}
$

From the above result, B varies with r i.e. field B is not uniform over the cross-section of the core because as we increase 'r' the B varies.

Recommended Topic Video

Solved Examples Based on Toroid

Example 1: The average radius of a toroid made on a ring of non-magnetic material is 0.1 m & it has 500 turns. If it carries 0.5A current, then the magnetic field produced along its circular axis inside the toroid will be

1) $25 \times 10^{-2} \mathrm{~T}$
2) $5 \times 10^{-2} \mathrm{~T}$
3) $25 \times 10^{-4} \mathrm{~T}$
4) $5 \times 10^{-4} \mathrm{~T}$

Solution:

Toroid

A toroid can be considered as a ring-shaped closed solenoid

wherein

$\begin{aligned} & B=\mu o n I \rightarrow_{\text {For toroid } \rightarrow \text { Circular solenoid }} \\ & n=\frac{N}{2 \pi R} \\ & B=\frac{\mu o N I}{2 \pi R} \Rightarrow \frac{4 \pi \times 10^{-7} \times 500 \times 0.5}{2 \pi \times 0.1} \\ & B=5 \times 10^{-4} T\end{aligned}$

Hence, the answer is the option (4).

Example 2: The current in the windings of the toroid is 2A. There are 400 turns & the mean circumferential length is 40cm. If the inside magnetic field is 1.0 T. The relative permeability is near to

1)400

2)200

3)300

4)100

Solution:

Toroid

$
B=\frac{\mu_{o N i}}{2 \pi r}=\mu_o n i
$
$B=\frac{\mu o \mu r N I}{2 \pi r} \rightarrow$ if $\mu r$ is also present
wherein
$
\begin{aligned}
& n=\frac{N}{2 \pi r} \\
& B=\frac{4 \pi \times 10^{-7} \times 400 \times \mu r \times 2}{0.4} \Rightarrow \mu r=400
\end{aligned}
$

Hence, the answer is the option (1).

Example 3: A toroidal solenoid has 3000 turns and a mean radius of 10 cm. It has a soft iron core with a relative permeability of 2000. What is the magnitude of the magnetic field in the core when a current of 1 A is passed through the solenoid?

1) 0.012 T
2) 0.12 T
3) 1.2 T
4) 12 T

Solution:

The magnetic field in the core is given by
$\mathrm{B}=\mu \mathrm{nI}$
where $\mu$ is the permeability of soft iron and n is the number of turns per unit length of the solenoid. Now
$\begin{aligned} & \mu_{\mathrm{r}}=\frac{\mu}{\mu_0} \text { and } \mathrm{n}=\frac{3000}{2 \pi \mathrm{r}}=\frac{3000}{2 \pi \times 0.1} \\ & \therefore \quad \mathrm{B}=\mu_{\mathrm{r}} \mu_0 \mathrm{nI} \\ & =2000 \times 4 \pi \times 10^{-7} \times \frac{3000}{2 \pi \times 0.1} \times 1=12 \mathrm{~T}\end{aligned}$

Hence, the answer is the option (4).

Example 4: A loosely wound helix made of stiff wire is mounted vertically with the lower end just touching a dish of mercury. When a current from the battery is started in the coil through the mercury :

1) The wire oscillates

2) The wire continues making contact

3) The wire breaks contact just when the current is passed

4) The mercury will expand by heating due to the passage of the current

Solution:

When a current is passed through the helix, the neighbouring coils of the helix attract each other due to which it contracts. As a result, the contact is broken and the coils will recover their original state under the influence of a restoring force. The contract is made again and the process continues. Thus, the wire oscillates.

Hence, the answer is the option (1).

Example 5: A toroid of mean radius ' a ', cross-section radius ' r ' and a total number of turns N. it carries a current ' i '. The torque experienced by the toroid if a uniform magnetic field of strength B is applied.

1) is zero
2) is $B i N \pi r^2$
3) is $B i N \pi a^2$
4) depends on the direction of the Magnetic field

Solution:

The torque is zero.

In a toroid, a magnetic field is present only inside the body with no magnetic field outside the body hence magnetic moment M=0 so it will not be affected by any other magnetic field hence torque experienced by the toroid will be 0.

so, the torque experienced by the toroid if a uniform magnetic field of strength B is zero.

Summary

A toroid, essentially a ring-shaped solenoid, confines magnetic fields within its core, making it ideal for applications like transformers and inductors. The magnetic field inside a toroid is determined by Ampere's circuital law and varies with the radial distance from the centre. In practical examples, toroids demonstrate their efficiency in minimizing electromagnetic interference and creating strong, uniform magnetic fields, essential for various electronic devices.