Transformers

Transformers are essential electrical devices used to transfer electrical energy between two or more circuits through electromagnetic induction. They play a crucial role in power distribution by stepping up voltage levels for efficient transmission over long distances and stepping down voltage levels for safe usage in homes and businesses. In real life, transformers are indispensable in ensuring a stable and reliable supply of electricity, enabling the functioning of everyday appliances, industrial machinery, and public infrastructure. This article explores the working principles, types, and practical applications of transformers, highlighting their significance in modern electrical systems.

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

This Story also Contains

1. Transformers
2. Solved Examples Based on Transformers
3. Summary

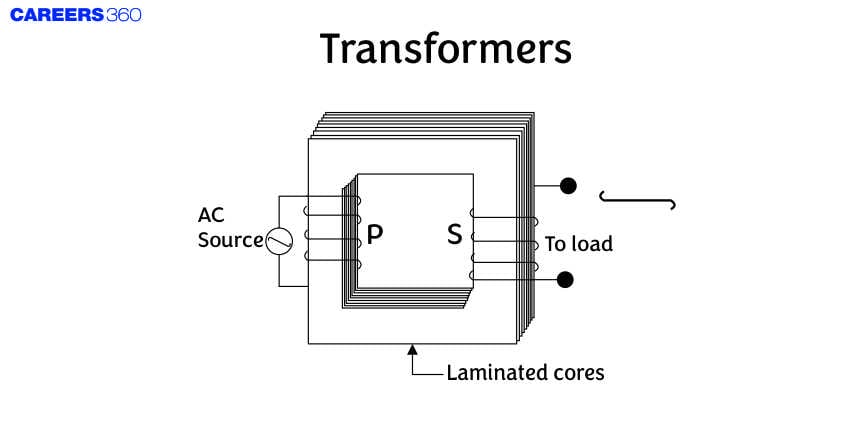
Transformers

Transformers are electrical devices designed to transfer electrical energy between two or more circuits through the principle of electromagnetic induction. They are essential components in power distribution networks, where they adjust voltage levels to ensure efficient transmission and safe usage. This is achieved by stepping up the voltage for long-distance transmission and stepping down the voltage for consumer use.

It is a device that raises or lowers the voltage in AC circuits through mutual induction. It consists of two coils wound on the same core. The alternating current passing through the primary creates a continuously changing flux through the core. This changing flux induces an alternating emf in the secondary.

Step-Up Transformer

A step-up transformer is a type of transformer designed to increase the voltage from the primary coil to the secondary coil. It is commonly used in power transmission systems to efficiently transfer electricity over long distances. By raising the voltage, step-up transformers minimize energy loss due to resistance in transmission lines.

A transformer in which the output (secondary) voltage is greater than its input (primary) voltage is called a step-up transformer.

Step-Down Transformer

A step-down transformer is designed to decrease the voltage from the primary coil to the secondary coil. This type of transformer is essential for delivering electricity at usable voltages to homes, businesses, and various electrical devices. By lowering the voltage, step-down transformers ensure that the electrical power is safe and suitable for everyday use.

A transformer in which the output (secondary) voltage is less than its input (primary) voltage is called a step-down transformer

• The transformer works on AC only and never on DC.
• It can increase or decrease either voltage or current but not both simultaneously.
• The transformer does not change the frequency of the input AC.
• There is no electrical connection between the winding but they are linked magnetically.
• Effective resistance between the primary and secondary winding is infinite.
• The flux per turn of each coil must be the same i.e.

$\phi_S=\phi_P \quad$ so, $-\frac{d \phi_P}{d t}=-\frac{d \phi_S}{d t}$

If $N_{P=\text { number of turns in primary }} N_S=$ number of turns in secondary,
$V_{P=}=$ applied (input) voltage to primary,
$V_S=$ Voltage across secondary (load voltage or output),
$e_{P=\text { induced emf in primary ; }}$
$e_S=$ induced emf in secondary,
$\phi=$ flux linked with primary as well as secondary, current in the primary;
$i_S=$ current in secondary (or load current)
As in an ideal transformer, there is no loss of power i.e. $P_{\text {out }}=P_{\text {in so, }}, V_S i_S=V_P i_P$ and $V_P \approx e_P, V_S \approx e_S$.
Hence,
$
\frac{e_S}{e_P}=\frac{N_S}{N_P}=\frac{V_S}{V_P}=\frac{i_P}{i_S}=k, \quad \mathrm{k}=\text { Transformation ratio. }
$

Efficiency of Transformer (η)

The efficiency of a transformer is a measure of how effectively it converts input electrical power into output electrical power. It is expressed as a percentage and is crucial in determining the transformer's performance and energy losses. The efficiency of a transformer is calculated using the following formula

For an ideal transformer, $P_{\text {out }}=P_{\text {in } \text { so }} \eta=100$.

For practical transformer, $P_{\text {in }}=P_{\text {out }}+P_{\text {losses }}$. The efficiency of a practical transformer lies between 70-90 %.

So $\eta=\frac{P_{\text {out }}}{\left(P_{\text {out }}+P_L\right)} \times 100=\frac{\left(P_{\text {in }}-P_L\right)}{P_{\text {in }}} \times 100$.

Losses in Transformers

Transformers are crucial in electrical power distribution and transmission, but they are not 100% efficient. The losses in transformers result in a reduction of the effective power delivered to the load compared to the input power. Understanding these losses helps in designing more efficient transformers and improving their operational performance.

Recommended Topic Video

Solved Examples Based on Transformers

Example 1: The core of any transformer is laminated so as to

1)reduce the energy loss due to eddy currents

2)make it light-weight

3)make it robust & strong

4)increase the secondary voltage.

Solution:

Transformer

It is a device that raises or lowers the voltage in an AC. circuits through mutual induction.

A laminated core reduces the energy loss due to eddy currents in a transformer.

Hence, the answer is the option (1).

Example 2: In the given ideal transformer

Find the voltage (in V) in the secondary coil.

1) 60

2)6.66

3)23

4)17

Solution:

Ideal transformer

There is no loss of power.

wherein

$\begin{aligned} & P_{\text {out }}=P_{\text {in }} \\ & V_s i_s^{\prime}=V_{\text {in }} i_{\text {in }}\end{aligned}$

In an ideal transformer, there is no power loss

$\begin{aligned} & \Rightarrow P_P=P_S \\ & \mathrm{~V}_{\mathrm{P}} \mathrm{l}_{\mathrm{P}}=\mathrm{v}_{\mathrm{S}} \mathrm{I}_{\mathrm{S}} \\ & 20 \times 3=\mathrm{v}_{\mathrm{S}} \times \mathrm{I} \\ & \mathrm{V}_{\mathrm{S}}=60 \mathrm{~V}\end{aligned}$

Hence, the answer is the option (1).

Example 3: A step-down transformer is used to

1)increase voltage & increase current

2)increase voltage & decrease current

3)decrease voltage & increase current

4)decrease voltage & decrease current

Solution:

Step down transformer If decrease voltage and increase current

$V_s<V_P$

In step down transformer no. of turns in the secondary coil is less than the primary coil. Hence less induced emf is produced. Therefore, a step-down transformer is used to decrease voltage & increase current.

$\begin{aligned} & V_S<V_P \\ & N_S<N_P \\ & I_S>I_P \\ & E_S<E_P\end{aligned}$

Hence, the answer is the option (3).

Example 4: A power transmission line feeds input power at 2300 V to a step-down transformer with its primary windings having 4000 turns. The output power is delivered at 230V by the transformer. If the current in the primary windings of the transformer is 5A and its efficiency is 90%, then the output current (in amperes) would be

1)45

2)35

3)50

4)25

Solution:

Efficiency of transformer

$\begin{aligned} \eta=\frac{P_{\text {out }}}{P_{\text {in }}} & =\frac{V_S I_S}{V_P I_P} \\ 0.9 & =\frac{23 I_S}{230 \times 5} \\ I_S & =45 \mathrm{~A}\end{aligned}$

Hence, the answer is the option (1).

Example 5: The efficiency of a practical transformer is

{where P_L = power loss }

1) $\frac{P_{\text {out }}}{P_{\text {out }}+P_L} \times 100$
2) $\frac{P_{\text {out }}}{P_{\text {out }}-P_L} \times 100$
3) $\frac{P_{\text {out }}+P_L}{P_{\text {out }}} \times 100$
4) $\frac{P_{\text {out }}-P_L}{P_{\text {out }}} \times 100$

Solution:

Practical transformer
$
P_{\text {in }}=P_{\text {out }}+P_{\text {loses }}
$

For practical transformers,
$
\begin{aligned}
& \mathrm{P}_{\text {in }}=\mathrm{P}_{\text {out }}+\mathrm{P}_{\text {loss }} \\
& { }_{\text {Now, }} \eta=\frac{P_{\text {out }}}{P_{\text {in }}}
\end{aligned}
$
$
\eta \%=\frac{P_{\text {out }}}{P_{\text {out }}+P_{\text {losses }}} \times 100
$

Hence, the answer is the option (1).

Summary

Transformers are essential electrical devices that transfer electrical energy between circuits via electromagnetic induction, playing a key role in power distribution by stepping up and stepping down voltage levels for efficient transmission and safe usage. Despite their importance, transformers are not 100% efficient due to core losses, copper losses, and other factors. Understanding these losses and optimizing transformer design improves efficiency, which is crucial for reliable electricity supply and minimizing energy wastage. Practical applications of transformers span from everyday household appliances to large-scale industrial machinery and public infrastructure, making them indispensable in modern electrical systems.