Youngs Modulus Elastic Modulus - Definition, Definition, Formula, Unit, FAQs

Youngs Modulus Elastic Modulus - Definition, Formula, Unit, FAQs

Edited By Team Careers360 | Updated on Nov 12, 2024 10:14 PM IST

Elastic constants are the values that determine the amount of deformation caused by a certain stress system acting on a material. Elastic constants come in a variety of forms, including:
Bulk modulus is a term that refers to the amount of (K)
Young’s modulus or elastic modulus, often known as the modulus of elasticity, is a measure of the elasticity of a material (E)
The Poisson Ratio (µ)
Modulus of stiffness or shear modulus (G)

JEE Main 2025: Physics Formula | Study Materials | High Scoring Topics | Preparation Guide

JEE Main 2025: Syllabus | Sample Papers | Mock Tests | PYQs | Study Plan 100 Days

NEET 2025: Syllabus | High Scoring Topics | PYQs

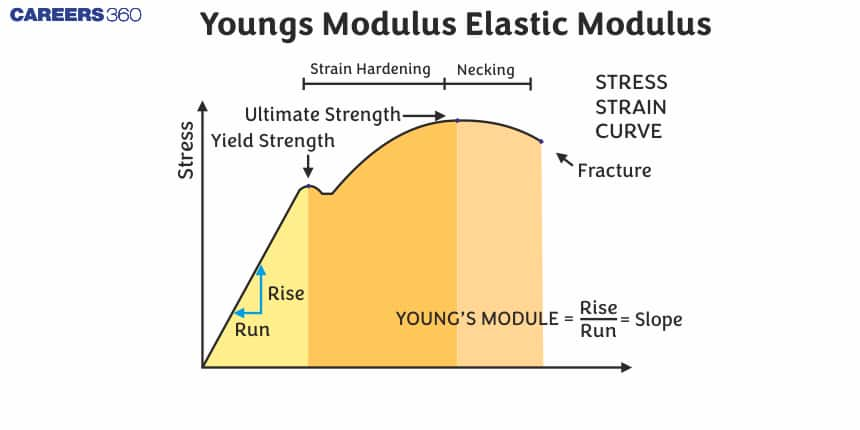
Youngs Modulus Elastic Modulus - Definition, Formula, Unit, FAQs

Also read -

What is young’s modulus of elasticity? Or define young’s modulus or elastic modulus

The mechanical property of material to tolerate compression/elongation with its length is defined as Young’s modulus, also called as modulus of elasticity. Also, young’s modulus is defined as the ratio of stress to strain.

It’s symbolised by letters E or Y.

Young’s modulus is a mechanical property of linear elastic solids such as rods, wires, and other similar objects. Other quantities, such as Bulk modulus and shear modulus, can be used to determine a material's elastic properties, but Young’s modulus is the most widely utilised. When a specific load is applied to a solid object, it deforms. When the pressure is removed from an elastic object, the body returns to its previous shape. Beyond a small degree of distortion, many materials are not linear and elastic. Only linear elastic materials have a constant Young’s modulus.

Young’s modulus formula is a mathematical formula that is used to calculate the modulus of

E=σ/ϵ

From Other Quantities: E=Modulus Young's Formula

=FL0/AΔL

ϵ = ΔL/L0

Young’s modulus formula E in Pa
? is the stress in Pa that is applied uniaxially.
ϵ is the proportionate deformation or the strain
The object under strain exerts a force called F.
A is the cross-sectional area of the actual cross-section.
L denotes the length variation.
The true length is L0.

SI Young’s modulus units	Pa
Imperial Unit	Pis
Dimension	ML^-1T^-2

YOUNG’S MODULUS= STRESS/STRAIN

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download E-book

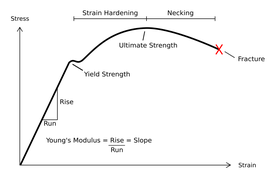
YOUNG’S MODULUS

The ratio of stress and strain, which corresponds to the material's stress, determines the Young’s modulus of such a material. The relationship is seen in the table below.

E =, where E is the material's Youngs formula in N/m2, is the stress applied to the material, and is the strain corresponding to the applied stress in the material. With the value of Young’s modulus for a material, the rigidity of a body may be determined. This is because it reveals the body's ability to resist deformation when force is applied.

Young’s modulus of steel 200,
glass has a value of 65,
wood has a value of 13, and
plastic (polystyrene) has a value of 3.

Related Topics Link,

Young’s modulus or elastic modulus factor-

We can assert that steel is more robust in nature than wood or polystyrene by studying its modulus of elasticity units, since it has a lower tendency to deform under applied load. Young’s modulus is also used to calculate how much a material will deform when subjected to a given load.

Another thing to remember is that the lower the Young’s modulus of a material, the greater the deformation experienced by the body, and in the case of clay and wood, this distortion might vary within a single sample. One part of the clay sample deforms more than the other, whereas a steel bar deforms evenly all the way around.

Also Read:

Elasticity definition or define elasticity or what is elasticity?

Elasticity is a term used in economics to describe how the aggregate quantity demanded of a good or service changes in response to price changes in that good or service. If the quantity demand for a product fluctuates more than proportionally when the price changes, the product is said to be elastic. Modulus of elasticity formula is ratio of stress by strain.

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. Determine the Young’s modulus of a material with an elastic stress of 4 N/m^2 and a strain of 0.15.

Given:

Stress = 4 N/m2

Strain = 0.15

The Young’s modulus formula is E = σ / ϵ

= 4 / 0.15 =26.66 N/m^2.

2. Give examples of dimensionless quantities.

Poison's ratio, Strain etc

3. What exactly is ductility?

Ductility is the property of a material that allows it to be pulled to a smaller portion when tensile stress is applied.

4. What is dimension of young modulus?

[ML^-1T^-2] is the dimensional formula for Young’s modulus.

5. What factors influence Young’s modulus?

The Young’s modulus of a substance is an unchangeable fundamental feature of all materials. Temperature and pressure, however, play a role. The Young’s modulus (or Elastic Modulus) is a measure of a material's stiffness. To put it another way, it refers to how easily it may be bent or stretched.

6. What is the significance of elastic modulus?

A material's Young’s modulus is a useful property to know in order to forecast how it will behave when subjected to a force. This is critical for practically everything in our environment, including buildings, bridges, automobiles, and more.