Algebraic Identities: Definition, Questions, Formula, Examples

Algebraic identities are powerful tools in mathematics that simplify complex expressions and solve equations efficiently. These identities, such as the difference of squares, the square of a sum, and the sum and difference of cubes, play a crucial role in various mathematical problems. Recognizing and applying these identities can transform complicated algebraic expressions into simpler forms, making problem-solving more manageable. This article explores topics like the application of algebraic identities in daily life, provides an algebraic identities chart, discusses how many algebraic identities are there, and includes algebraic identities formulas.

What are Algebraic Identities?

Definition: Algebraic identities are equations that hold true for all values of the variables within them. They provide a standard way to transform expressions and solve problems more efficiently.

Example: One of the most common algebraic identities is $(a+b)^2=a^2+2ab+b^2$, this identity is true for any values of $a$ and $b$.

Algebraic Identities of Two Variables

The identities involving two variables $a$ and $b$ are as follows:

• $(a+b)^2=a^2+2ab+b^2$

• $(a-b)^2=a^2-2ab+b^2$

• $a^2+b^2=(a+b)^2-2ab=(a-b)^2+2ab$

• $a^2-b^2=(a+b)(a-b)$

• $(x+a)(x+b)=x^2+(a+b)x+ab$

• $(a+b)^3=a^3+3a^2b+3ab^2+b^3=a^3+b^3+3ab(a+b)$

• $(a-b)^3=a^3-3a^2b+3ab^2-b^3=a^3-b^3-3ab(a-b)$

• $a^3+b^3=(a+b)(a^2-ab+b^2)$

• $a^3-b^3=(a-b)(a^2+ab+b^2)$

Algebraic Identities of Three Variables

The identities involving three variables $a$, $b$ and $c$ are as follows:

• $(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

• $a^2+b^2+c^2=(a+b+c)^2-2ab-2bc-2ca$

• $a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$

• If $a+b+c=0$, then $a^3+b^3+c^3=3abc$

Algebraic Identities used for factorisation

Some algebraic identities are often used to factorise polynomials, making it easier to solve equations. These identities are as follows:

• $a^2-b^2=(a+b)(a-b)$

• $x^2+(a+b)x+ab=(x+a)(x+b)$

• $a^3+b^3=(a+b)(a^2-ab+b^2)$

• $a^3-b^3=(a-b)(a^2+ab+b^2)$

Proof of some standard Algebraic Identities

Let us also take a look at the derivation of some important identities and understand clearly how they came to be.

Proof of (x + a)(x + b) = x2 + x(a + b) + ab

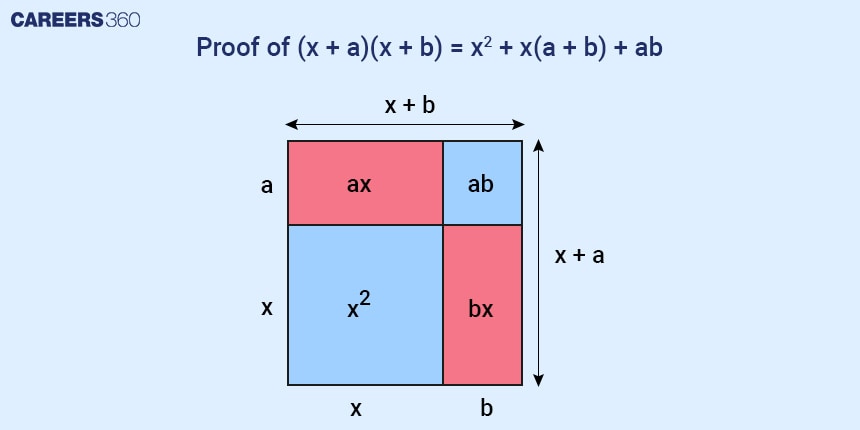
(x+a)(x+b) is nothing but the area of a rectangle whose sides are (x+a) and (x+b), respectively.

This area of the rectangle can be divided into four parts i.e. the area of the square with sides x, the area of one rectangle with sides x and a, the area of one rectangle with sides x and b, and the area of one rectangle with sides a and b.

Summing all these areas we have x2 + ax + bx + ab. This gives us the proof for the algebra identity (x + a)(x + b) = x2 + ax + bx + ab = x2 + x(a + b) + ab.

Proof of (a + b)2 = a2 + 2ab + b2

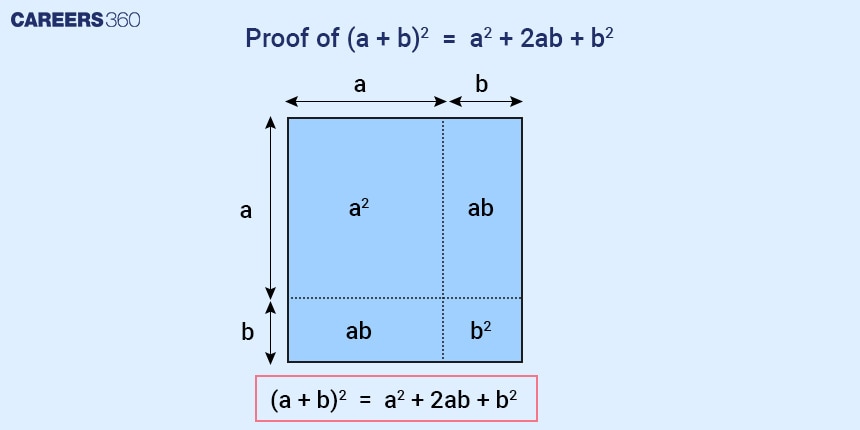
(a + b)2 is nothing but the area of a square whose sides are (a+b).

This area of the square can be divided into four parts i.e. the area of the square with sides a, the area of two rectangles with sides a and b, and the area of one square with sides b.

Summing all these areas we have a2 + ab + ab + b2. This gives us the proof for the algebra identity (a + b)2 = a2 + ab + ab + b2 = a2 + 2ab + b2.

Proof of (a + b)(a - b) = a2 - b2

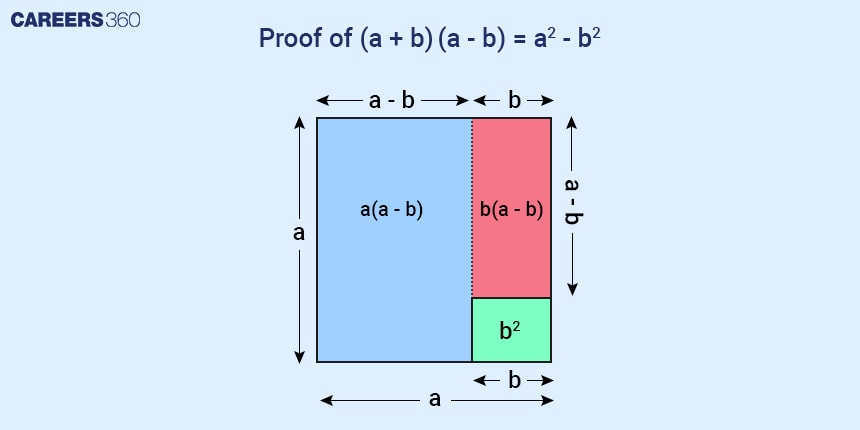
a2 - b2 is the difference of the areas of two squares of sides ‘a’ and ‘b’, which is equal to the sum of the two rectangles shown in the figure. One rectangle has a length of ‘a’ units and a breadth of (a - b) units. Another rectangle is taken with a length of (a - b) and a breadth of ‘b’ units.

Now, the sum of the two rectangles = a(a - b) + b(a - b) which is equal to a2 - b2.

Therefore, a2 - b2 = a(a - b) + b(a - b) = (a + b)(a - b)

Hence, a2 - b2 = (a + b)(a - b).

Proof of (a − b)2 = a2 − 2ab + b2

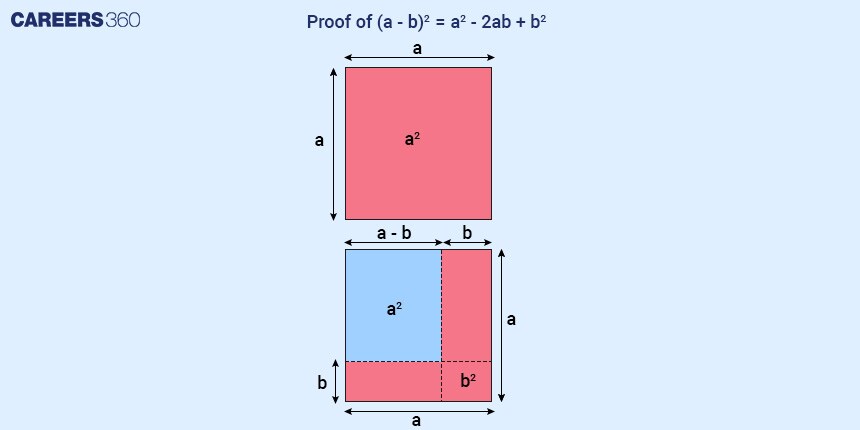
Let’s think of (a - b)2 as the area of a square with length (a - b).

To understand this, let's begin with a large square of area a2. We need to reduce the length from the sides by b, and it becomes a square with a length of (a - b). We now have to remove the extra bits from a2 to be left with (a - b)2. In the figure below, (a - b)2 is shown by the light blue area. To get the light blue square from the larger orange square, we have to subtract the vertical and horizontal rectangles that have the area of ‘ab’.

However, removing ‘ab’ twice will also remove the overlapping square at the bottom right corner twice. So, we will also have to add b2. Thus we have (a − b)2 = a2 − ab − ab + b2.

Hence this proves the algebraic identity (a − b)2 = a2 − 2ab + b2.

List of All Algebraic Identities

Application of Algebraic Identities

• Simplifying Expressions: We can reduce the complexity of algebraic expressions and factorise large polynomials with the help of algebraic identities.

• Solving Equations: We can solve quadratic and higher-degree equations by using the identities.

• Geometric Calculations: These identities also help us calculate the areas and volumes of geometric shapes easily.

• Probability and Statistics: We can derive formulas for variance and standard deviation and also simplify complex expressions using the identities.

• Trigonometry: Using these identities we can also simplify trigonometric expressions and prove trigonometric formulas.

• Computer Science: We can optimize algorithms and design error-detecting or correcting codes with the help of these identities.

• Economics and Finance: We can also derive and simplify formulas for compound interest and solve optimization problems using algebraic identities.

These applications demonstrate the versatility and importance of algebraic identities across various fields.

Difference Between Algebraic Expression and Algebraic Identities

An algebraic expression is a combination of variables, constants, and operations (addition, subtraction, multiplication, division). Examples include $2x + 3, a^2+5b, m-\frac{n}{2}$ etc.

An algebraic identity is an equation that is true for all values of the variables involved.

For example, $(a+b)^2=a^2+2ab+b^2$, is true for all values of ‘a’ and ‘b’.

The main difference is that algebraic expressions vary with variable inputs, while algebraic identities are universally true.

Tips and Tricks

• Memorize key identities for quick recall.

• Practice factorizing different expressions using identities.

• Look for patterns or similarities in expressions that suggest the use of specific identities.

• Be mindful of common mistakes such as incorrect application of signs or forgetting some terms completely.

• Sometimes, substituting values for variables can simplify expressions and make it easier to apply identities.

Practice Questions/Solved Examples

Q.1.

If x + y = √3 and x – y = √2, the value of 8xy(x2 + y2) is:

1. 6

2. √6

3. 5

4. √5

Hint: Apply the formulas given below:

(x + y)2 = x2 + y2 + 2xy

(x – y)2 = x2 + y2 – 2xy

Solution:

According to the question,

x + y = √3

Squaring both sides, we get,

⇒ x2 + y2 + 2xy = 3 ––––––––––––(i)

Now, x – y = √2

Squaring both sides, we get,

⇒ x2 + y2 – 2xy = 2 ––––––––––––(ii)

Adding equations (i) and (ii), we get,

2x2 + 2y2 = 5

⇒ x2 + y2 = $\frac{5}{2}$ ––––––––––––––––(iii)

Now putting the value from equation (iii) in equation (i), we get,

$\frac{5}{2}$ + 2xy = 3

⇒ 2xy = 3 – $\frac{5}{2}$

⇒ 2xy = $\frac{1}{2}$

$\therefore$ xy = $\frac{1}{4}$

Now, the value of 8xy(x2 + y2)

= $8 × \frac{1}{4} × \frac{5}{2}$

= $5$

Hence, the correct answer is option (3).

Q.2.

If $(a+b-6)^{2}+a^{2}+b^{2}+1+2b=2ab+2a$, the value of $a$ is:

1. 7

2. 6

3. 3.5

4. 2.5

Hint: Use the formula: $(a-b-c)^{2}=a^{2}+b^{2}+c^{2}-2ab+2bc-2ac$

Solution:

Given:

$(a+b-6)^{2} + a^{2}+b^{2}+1+2b = 2ab + 2a$

⇒ $(a+b-6)^{2}+a^{2}+ b^{2}+1+2b-2ab-2a = 0$

⇒ $(a+b-6)^{2}+ a^{2}+ (-b)^{2}+ (-1)^{2}+2a (-b) +2 (-b) (-1)+2 (a) (-1)=0$

⇒ $ (a + b-6)^{2}+(a-b-1)^{2}=0$

⇒ $a+b-6 = 0$ and $a-b-1=0$ [if the sum of the squares of two numbers are zero then each of them will also be zero]

⇒ $a+b = 6$ and $a-b = 1$

On adding these two equations,

$a+b+a-b = 6+1$

⇒ $2a = 7$

⇒ $a=\frac{7}{2}=3.5$

Hence, the correct answer is option (3).

Q.3.

If $a^{2}+13b^{2}+c^{2}-4ab-6bc=0$, then $a:b:c$ is:

1. $1:2:3$

2. $2:1:3$

3. $2:3:1$

4. $3:2:1$

Hint: Use this formula: $a^{2}-2ab+b^{2}=(a-b)^{2}$

Solution:

Given: $a^{2} + 13b^{2} + c^{2} - 4ab - 6bc = 0$

⇒ $a^{2} - 4ab + 4b^{2} + 9b^{2} + c^{2} - 6bc = 0$

⇒ $a^{2} - 4ab + 4b^{2} + c^{2} - 6bc + 9b^{2} = 0$

⇒ $(a - 2b)^{2} + (c - 3b)^{2} = 0$

⇒ $a - 2b = 0$ and $c - 3b = 0$ [if the sum of the squares of two numbers is zero then each of the numbers will also be zero]

⇒ $a = 2b$ and $c = 3b$

⇒$a:b = 2: 1$ and $b : c = 1: 3$

$\therefore a:b:c = 2:1:3$

Hence, the correct answer is option (2).

Q.4.

If $\left ( a+\frac{1}{a} \right )^{2}=3$, then the value of $\left ( a^{2}+\frac{1}{a^{2}} \right )$ will be:

1. 0

2. 1

3. 2

4. 3

Hint: Use this formula: $(a+b)^2=a^2+2ab+b^2$

Solution:

Given:

$(a+\frac{1}{a})^2=3$

Expanding the left side of the equation:

⇒ $a^2 + 2(a)(\frac{1}{a}) + \left(\frac{1}{a}\right)^2 = 3$

⇒ $a^2 + 2 + \frac{1}{a^2} = 3$

⇒ $a^2 + \frac{1}{a^2} = 3 - 2$

⇒ $a^2 + \frac{1}{a^2} = 1$

Therefore, the value of $a^2 + \frac{1}{a^2}$ is 1.

Hence, the correct answer is option (2).

Q.5.

If $(a-2)+\frac{1}{(a+2)} =-1$, the value of $\left (a+2 \right )^{2}+\frac{1}{(a+2)^{2}}$ is:

1. 7

2. 11

3. 23

4. 27

Hint: Frame this equation as $(a+2)+\frac{1}{(a+2)}=3$ and use the following formula.

$(a+b)^2=a^2+b^2+2ab$

Solution:

Given:

$(a-2)+\frac{1}{(a+2)} =-1$

⇒ $(a+2)+\frac{1}{(a+2)}=3$ (Adding 4 on both sides)

Square both sides and use the formula, $(a+b)^2=a^2+b^2+2ab$

⇒ $(a+2)^2+(\frac{1}{(a+2)})^2+2(a+2)(\frac{1}{(a+2)})=9$

⇒ $(a+2)^2+(\frac{1}{(a+2)})^2+2=9$

⇒$(a+2)^2+\frac{1}{(a+2)^2}=9-2$

⇒$(a+2)^2+\frac{1}{(a+2)^2}=7$

Hence, the correct answer is 7.

Q.6.

If a + b = 5 and a – b = 3, then the value of (a2 + b2) is:

1. 17

2. 18

3. 19

4. 20

Hint: Find the values of a and b then use them in the given expression, (a2 + b2).

Solution:

Given:

a + b = 5 -----------------------(i)

a – b = 3 ----------------------(ii)

Add both equations (i) and (ii),

⇒ a + b + a – b = 5 + 3

⇒ 2a = 8

⇒ a = 4

From equation (i),

⇒ 4 + b = 5

⇒ b = 5 – 4

⇒ b = 1

Now, a2 + b2 = 42 + 12 = 16 + 1 = 17

Hence, the correct answer is option (1).

Q.7.

If a + b + c = 0, the value of (a3 + b3 + c3) is:

1. abc

2. 2abc

3. 3abc

4. 0

Hint: Use this formula

a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)

Solution:

Given: a + b + c = 0

a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)

⇒ a3 + b3 + c3 – 3abc = (0)(a2 + b2 + c2 – ab – bc – ca)

⇒ a3 + b3 + c3 – 3abc = 0

⇒ a3 + b3 + c3 = 3abc

Hence, the correct answer is option (3).

Q.8.

If $\frac{1}{p}+\frac{1}{q}=\frac{1}{p+q}$, the value of $\left (p^{3}-q^{3}\right )$ is:

1. $p-q$

2. $pq$

3. $1$

4. $0$

Hint: Use the formula given below:

$\left (p^{3}-q^{3}\right)=(p-q)(p^2+q^2+pq)$

Solution:

Given:

$\frac{1}{p}+\frac{1}{q}=\frac{1}{p+q}$

⇒ $\frac{q+p}{pq}=\frac{1}{p+q}$

⇒ $(p+q)^2=pq$

⇒ $p^2+q^2+2pq=pq$

⇒ $p^2+q^2+pq=0$ ----------------------------(i)

Now, $\left (p^{3}-q^{3}\right )=(p-q)(p^2+q^2+pq)$

Putting the value of $p^2+q^2+pq=0$ from the equation (i)

So, $\left (p^{3}-q^{3}\right)=(p-q)(0)$

⇒ $\left (p^{3}-q^{3}\right)=0$

Hence, the correct answer is option (4).

Q.9.

If the square of the sum of three positive consecutive natural numbers exceeds the sum of their squares by 292, what is the largest of the three numbers?

1. 5

2. 6

3. 3

4. 8

Hint: The consecutive natural numbers are a = (x – 1), b = x, and c = (x + 1).

Use the formula given below:

(a + b + c)2 = (a2 + b2 + c2 + 2ab + 2bc + 2ca)

Solution:

The consecutive natural numbers are a = (x – 1), b = x, and c = (x + 1).

According to the question,

(a + b + c)2 – (a2 + b2 + c2) = 292

⇒ a2 + b2 + c2 + 2ab + 2bc + 2ca – a2 – b2 – c2 = 292

⇒ ab + bc + ca = 146

⇒ (x)(x – 1) + (x)(x + 1) + (x + 1)(x – 1) = 146

⇒ x2 – x + x2 + x + x2 – 1 = 146

⇒ 3x2 = 147

⇒ x2 = $\frac{147}{3}$

⇒ x2 = 49

⇒ x = 7

So, the largest number is (x + 1) = 8

Hence, the correct answer is option (4).

Q.10.

If $x+\frac{1}{x}=\sqrt{3}$, the value of $\left (x^{3}+\frac{1}{x^{3}} \right )$ is:

1. $\sqrt{3}$

2. $\frac{1}{\sqrt{3}}$

3. $0$

4. $1$

Hint: Cube both sides of the equation and use the formula given below:

$(a+b)^3=a^3+b^3+3ab(a+b)$

Solution:

Given: $x+\frac{1}{x}=\sqrt{3}$

Cubing both sides and simplifying the equation,

⇒ $(x+\frac{1}{x})^3=(\sqrt{3})^3$

⇒ $x^3+\frac{1}{x^3}+3(x×\frac{1}{x})(x+\frac{1}{x})=(\sqrt{3})^3$

⇒ $x^3+\frac{1}{x^3}+3(x+\frac{1}{x})=3\sqrt{3}$

Putting the value of $x+\frac{1}{x}=\sqrt{3}$

⇒ $x^3+\frac{1}{x^3}+3\sqrt{3}=3\sqrt{3}$

⇒ $x^3+\frac{1}{x^3}=3\sqrt{3}-3\sqrt{3}$

⇒ $x^3+\frac{1}{x^3}=0$

Hence, the correct answer is option (3).