Bodmas Rule in Simplification

Arithmetic operations on two numbers are straightforward. However, when dealing with multiple arithmetic operations involving several numbers, we need guidance from acronyms like BODMAS, BIDMAS, and PEDMAS to ensure we perform the operations in the correct order. In this article, we will learn how to simplify using the BODMAS rule in an elaborate way to make it easy and useful for all the students. BODMAS simplification is one of the most useful topics in any competitive examination in India.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. Explaining the BODMAS rule in simplification
2. Understanding the rule of BODMAS
3. Meaning and Order of Operators in BODMAS
4. Understanding the rule of BIDMAS
5. Meaning and Order of Operators in BIDMAS
6. Understanding the rule of PEDMAS
7. Meaning and Order of Operators in PEDMAS
8. Application of BODMAS in Simplification Problems
9. Tips and tricks related to BODMAS
10. Practice Questions

• BODMAS stands for Brackets, Of, Division, Multiplication, Addition, and Subtraction.

• BIDMAS stands for Brackets, Indices (which is another term for powers and roots), Division, Multiplication, Addition, and Subtraction.

• PEDMAS stands for Parentheses, Exponents(Which are powers or indices), Division, Multiplication, Addition, and Subtraction.

These acronyms help us navigate complex calculations by defining a clear sequence for performing operations, thus avoiding ambiguity and ensuring accurate results.

Explaining the BODMAS rule in simplification

BODMAS rule helps to operate in the correct order to simplify an expression to get the value. Using this acronym, we get a clear picture of what operations need to be first, which after that, and which at the end.

Now we will take an example and see the step-by-step usage of BODMAS on an expression to simplify.

Steps to simplify using BODMAS rule

Simplify the following expression using the BODMAS rule:
41 × 3 – 8 ÷ 2 – 16 of (7 – 2) + (3 × 5 – 4)

Step 1: Brackets operation

First, operate on the terms that are inside the Brackets.

i.e., (7 – 2) = 5 and (3 × 5 – 4) = 11

Expression become: 41 × 3 – 8 ÷ 2 – 16 of 5 + 11

Step 2: “Of” operation

Then as per the BODMAS rule, multiplication of the numbers indicated by “of”.

i.e., 16 of 5 = 16 × 5 = 80

Expression become: 41 × 3 – 8 ÷ 2 – 80 + 11

Step 3: Division operation

Perform the division method from left to right.

i.e., 8 ÷ 2 = 4

Expression become: 41 × 3 – 4 – 80 + 11

Step 4: Multiplication operation

Perform the multiplication method from left to right.

i.e., , 41 × 3 = 123

Expression become: 123 – 4 – 80 + 11

Step 5: Addition operation

Now, we will add the positive terms and negative terms separately.

Expression become: 134 – 84

Step 6: Subtraction operation

At the end, we will do subtraction from left to right in the expression.

i.e., 134 – 84 = 50

Hence, the value of the expression is 50.

As we can see, using the BODMAS rule, we can simplify expressions easily.

Understanding the rule of BODMAS

The BODMAS rule is used to simplify and get the value of an expression if it has brackets, “of”, and arithmetic operations like addition, subtraction, multiplication, and division. It helps us to remember which operations to do first.

When faced with a mathematical expression involving multiple types of brackets, “of”, and arithmetic operations, knowing which operation to perform first can be challenging. This confusion can lead to incorrect results and wasted time without a clear method.
The BODMAS rule provides a straightforward approach to handle these expressions systematically.

First, do the brackets' operations, then evaluate and multiply the numbers where “of” is written. After that, we will divide and multiply from left to right in that order. Addition comes next and Subtraction at the end. Both these operations should be done from left to right.

Meaning and Order of Operators in BODMAS

1. Brackets (B):

In mathematics, if a symbol is used to group parts of an expression or equation, it is called Brackets.

It indicates that the operations within the brackets should be performed first according to the order of operations.

There are three main types of brackets.

• First brackets or parentheses, ()

• Second brackets or curly braces, {}

• Third brackets or square brackets, []

If an expression has all three brackets in it, then the order of operations should be
first brackets > second brackets > third brackets.

2. Of (O):

In mathematical expressions, the term "of" means multiplication. So, after completing the operations within brackets, the next step is multiplying the numbers wherever the term "of" appears.

3. Division (D):

The division is one of the four basic arithmetic operations. It is the process of determining how many times one number is contained within another. It will be done from left to right in the expression.

4. Multiplication (M):

Multiplication is one of the four basic arithmetic operations. It is the process of repeatedly adding the same number. It will be done from left to right in the expression.

5. Addition (A):

Addition is a fundamental operation of the four basic arithmetic operations. It is the process of getting a total sum by combining two or more numbers. It will be done from left to right in the expression.

6. Subtraction (S):

Subtraction is a fundamental operation of the four basic arithmetic operations. It is the process of finding the difference between two numbers by removing the value of one number from another. It will be done from left to right in the expression.

Understanding the rule of BIDMAS

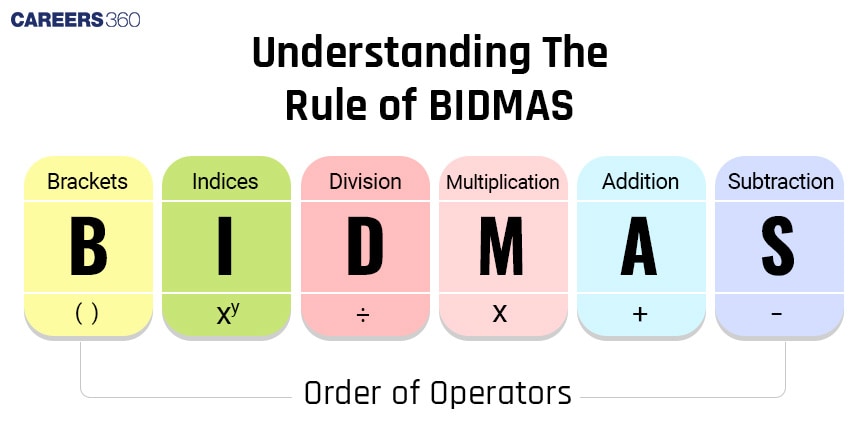
The BIDMAS rule is used to simplify and get the value of an expression if it has brackets, indices, and arithmetic operations like addition, subtraction, multiplication, and division. It helps us to remember which operations to do first.

When faced with a mathematical expression involving multiple types of brackets, indices, and arithmetic operations, knowing which operation to perform first can be challenging. This confusion can lead to incorrect results and wasted time without a clear method.
The BIDMAS rule provides a straightforward approach to handle these expressions systematically.

First, the operations of brackets are done, and then the exponents or roots are evaluated. After that, we will divide and multiply from left to right in that order. Addition comes next and Subtraction at the end. Both these operations should be done from left to right.

Meaning and Order of Operators in BIDMAS

1. Brackets (B):

In mathematics, if a symbol is used to group parts of an expression or equation, it is called Brackets.

It indicates that the operations within the brackets should be performed first according to the order of operations.

There are three main types of brackets.

• First brackets or parentheses, ()

• Second brackets or curly braces, {}

• Third brackets or square bracket, []

If an expression has all three brackets in it, then the order of operations should be
first brackets > second brackets > third brackets.

2. Indices (I):

Indices or exponents represent the power or roots of numbers and need to be simplified to their standard form.

For example, 22 simplifies to 4, and 52 simplifies to 25.

3. Division (D):

The division is one of the four basic arithmetic operations. It is the process of determining how many times one number is contained within another. It will be done from left to right in the expression.

4. Multiplication (M):

Multiplication is one of the four basic arithmetic operations. It is the process of repeatedly adding the same number. It will be done from left to right in the expression.

5. Addition (A):

Addition is a fundamental operation of the four basic arithmetic operations. It is the process of getting a total sum by combining two or more numbers. It will be done from left to right in the expression.

6. Subtraction (S):

Subtraction is a fundamental operation of the four basic arithmetic operations. It is the process of finding the difference between two numbers by removing the value of one number from another. It will be done from left to right in the expression.

Understanding the rule of PEDMAS

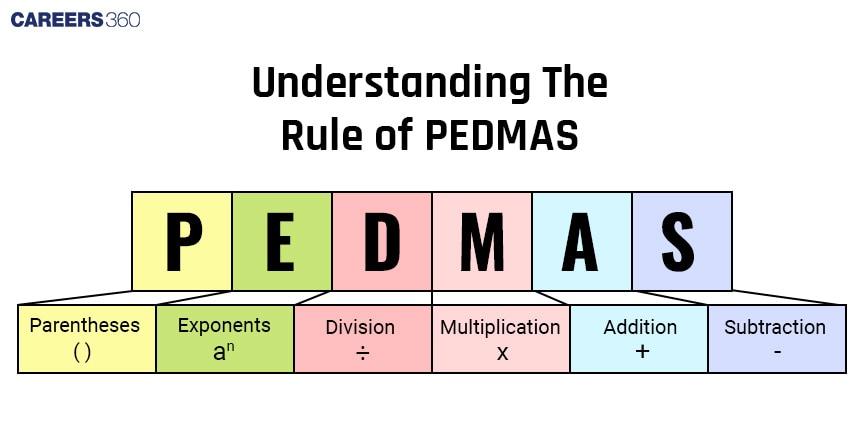
The PEDMAS rule is used to simplify and get the value of an expression if it has parentheses, exponents, and arithmetic operations like addition, subtraction, multiplication, and division. It helps us to remember which operations to do first.

When faced with a mathematical expression involving multiple types of parentheses, exponents, and arithmetic operations, knowing which operation to perform first can be challenging. This confusion can lead to incorrect results and wasted time without a clear method.
The PEDMAS rule provides a straightforward approach to handle these expressions systematically.

First, do the operations of parentheses, and then evaluate the exponents or roots. After that, we will divide and multiply from left to right in that order. Addition comes next and Subtraction at the end. Both these operations should be done from left to right.

Meaning and Order of Operators in PEDMAS

1. Parentheses (P):

Parentheses generally mean the Brackets “()”. But in mathematical expressions, we also have to evaluate other grouping symbols like square brackets “[]” and curly braces “{}”.

2. Exponents (E):

Exponents represent the power or roots of numbers and need to be simplified to their standard form.

For example, 22 simplifies to 4, and 52 simplifies to 25.

3. Division (D):

The division is one of the four basic arithmetic operations. It is the process of determining how many times one number is contained within another. It will be done from left to right in the expression.

4. Multiplication (M):

Multiplication is one of the four basic arithmetic operations. It is the process of repeatedly adding the same number. It will be done from left to right in the expression.

5. Addition (A):

Addition is a fundamental operation of the four basic arithmetic operations. It is the process of getting a total sum by combining two or more numbers. It will be done from left to right in the expression.

6. Subtraction (S):

Subtraction is a fundamental operation of the four basic arithmetic operations. It is the process of finding the difference between two numbers by removing the value of one number from another. It will be done from left to right in the expression.

Application of BODMAS in Simplification Problems

• Simplify the following expression using the BODMAS rule:
• {1 + 7 + (16 ÷ 8 ÷ 2)} + {(6 × 22 + 6) × $\frac{2}{6}$}
• Here, there are two types of brackets, first brackets and curly braces.
• First, operate on the terms that are inside the first brackets from left to right.
• i.e., (16 ÷ 8 ÷ 2) = 1 and (6 × 22 + 6) = 30
• Expression becomes: {1 + 7 + 1} + {30 × $\frac{2}{6}$}
• Now, operation on the terms of curly braces will be done.
• i.e., {1 + 7 + 1} = 9 and {30 × $\frac{2}{6}$} = 10
• Expression becomes: 9 + 10
• Finally, Addition can be done.
• 9 + 10 = 19
• Hence, the value of the expression is 19.

• What is the value of 2160 × 3 ÷ 144 + 13 - 2?

• In this expression, there are no brackets, only arithmetic operations are there.
• So, as per the BODMAS rule,
• First, we will do Division, then multiplication from left to right.
• i.e., $2160 × \frac{3}{144}=45$
• Expression becomes: 45 + 13 - 2
• Now, Addition and Subtraction will be done from left to right.
• 45 + 13 - 2 = 56
• Hence, the value of the expression is 56.

Tips and tricks related to BODMAS

• We can remember the BODMAS rule by the sentence “Billy Orders Dosa Monday And Saturday”.

• The first operation on the expression should always be digits inside the Brackets.

• The order of the Brackets will be, first brackets, () > second brackets, {} > third brackets, []

• Then, multiply the digits where “of” is written or evaluate the exponents.

• Perform division and multiplication from left to right.

• Perform addition and subtraction from left to right.

• If there is a negative sign just before a bracket then open the bracket, and multiply the negative sign with each term inside the bracket.
  4 – (12 + 3) ⇒ 4 – 12 – 3

• If there is any nonzero term in the multiplication of the bracket, multiply that term with each term inside the bracket.
  7(4x + 2) ⇒ 28x + 14

Practice Questions

Q1. Simplify the following using BODMAS rule:
(16 + 14) ÷ 2 – 12 + 16 × 4 – 28 + 13 (–16 + 13)

1. 6

2. 0

3. -3

4. 3

Answer:

Given: (16 + 14) ÷ 2 – 12 + 16 × 4 – 28 + 13 (–16 + 13)

Using the BODMAS rule, we get,

= 30 ÷ 2 – 12 + 16 × 4 – 28 + 13 (–3)

= 15 – 12 + 64 – 28 – 39

= 3 + 64 – 67

= 0

Hence, the correct answer is option(B).

Q2. What is the value of $\frac{3}{2} \div \frac{1}{7} \times[(\frac{1}{2} - \frac{1}{3}) \div \frac{1}{42}]?$

1. $72 \frac{1}{3}$

2. $73 \frac{1}{2}$

3. $72 \frac{1}{2}$

4. $71 \frac{2}{3}$

Answer:

Given: $\frac{3}{2} \div \frac{1}{7} \times[(\frac{1}{2} - \frac{1}{3}) \div \frac{1}{42}]$

Applying the BODMAS rule, we get,

$=\frac{3}{2} \div \frac{1}{7} \times[(\frac{3-2}{6}) \div \frac{1}{42}]$

$=\frac{3}{2} \div \frac{1}{7} \times[\frac{1}{6} \div \frac{1}{42}]$

$=\frac{3}{2} \div \frac{1}{7} \times[\frac{1}{6} \times{42}]$

$=\frac{3}{2} \div \frac{1}{7} \times7$

$=\frac{21}{2}\times 7$

$=\frac{147}{2}$

$=73\frac{1}{2}$

Hence, the correct answer is $73\frac{1}{2}$.

Q3. If $M =\left ( \frac{3}{7} \right ) ÷ \left ( \frac{6}{5} \right ) ×\left ( \frac{2}{3} \right ) + \left ( \frac{1}{5} \right ) ×\left ( \frac{3}{2} \right )$ and $N = \left ( \frac{2}{5} \right ) × \left ( \frac{5}{6} \right ) ÷ \left ( \frac{1}{3} \right ) + \left ( \frac{3}{5} \right ) × \left ( \frac{2}{3} \right ) ÷ \left ( \frac{3}{5} \right )$, then what is the value of $\frac{M}{N}$?

1. $\frac{207}{560}$

2. $\frac{339}{1120}$

3. $\frac{113}{350}$

4. $\frac{69}{175}$

Answer:

$M =\left (\frac{3}{7}\right) ÷ \left (\frac{6}{5} \right) ×\left (\frac{2}{3} \right) + \left (\frac{1}{5} \right) ×\left (\frac{3}{2}\right)$

$M =\left (\frac{3}{7} \right) × \left (\frac{5}{6} \right) ×\left (\frac{2}{3} \right) + \left (\frac{1}{5} \right) ×\left (\frac{3}{2} \right)$

$M = \frac{5}{21}+\frac{3}{10}$

$M = \frac{113}{210}$

$N = \left (\frac{2}{5} \right) × \left (\frac{5}{6} \right) ÷ \left (\frac{1}{3} \right) + \left (\frac{3}{5} \right) × \left (\frac{2}{3} \right) ÷ \left (\frac{3}{5} \right)$

$N = \left (\frac{2}{5} \right) × \left (\frac{5}{6} \right) ×3+ \left (\frac{3}{5} \right) × \left (\frac{2}{3} \right) × \left (\frac{5}{3} \right)$

$N =1 + \left (\frac{2}{3} \right)$

$N = \left (\frac{5}{3} \right)$

$\frac{M}{N} = \frac{113}{210}×\frac{3}{5} = \frac{113}{350}$

Hence, the correct answer is $\frac{113}{350}$.

Q4. Simplify the following using BODMAS rule:

$\{[(x-5)(x-1)]-[(9 x-5)(9x-1)]\} \div 16x$

1. $2x(5x-3)$

2. $-(5x-3)$

3. $x(5x-3)$

4. $-6x(5x-3)$

Answer:

Given: $\{[(x-5)(x-1)]-[(9 x-5)(9x-1)]\} \div 16x$

$= [(x^{2}-x-5x+5)-[(81x^{2}-9x-45x+5)]\div 16x$

$= [(x^{2}-6x+5)-[(81x^{2}-54x+5)]\div 16x$

$= [(x^{2}-6x+5-81x^{2}+54x-5)]\div 16x$

$= [-80x^{2}+48x]\div 16x$

$=[-5x+3]$

$=-(5x-3)$

Hence, the correct answer is $-(5x-3)$.

Q5. If $\left(2^2+4\right)^2 \times(3-5)+20 \%$ of $400+x \%$ of $30=30 \%$ of $30$, find the value of $x$.

1. 150

2. 120

3. 190

4. 160

Answer:

$\left(2^2+4\right)^2 \times(3-5)+20 \%$ of $400+x \%$ of $30=30 \%$ of $30$

⇒ $(4+4)^2 \times (-2) + \frac{20\times 400}{100} + \frac{30x}{100} = \frac{30\times 30}{100}$

⇒ $8^2 \times (-2) + 80 + 0.3x = 9$

⇒ $-128 + 80 + 0.3 x = 9$

⇒ $-48 + 0.3x = 9$

⇒ $0.3x = 57$

$\therefore x = \frac{570}{3} = 190$

Hence, the correct answer is 190.

Q6. Simplify the following expression.

$\frac{7}{10} \div \frac{3}{7}$ of $\left(2 \frac{3}{10}+2 \frac{3}{5}\right)+\frac{1}{5} \div 1 \frac{2}{5}-\frac{2}{7}$

1. $-\frac{4}{21}$

2. $\frac{5}{21}$

3. $\frac{4}{21}$

4. $-\frac{5}{21}$

Answer:

$\frac{7}{10} \div \frac{3}{7}$ of $\left(2 \frac{3}{10}+2 \frac{3}{5}\right)+\frac{1}{5} \div 1 \frac{2}{5}-\frac{2}{7}$

Converting mixed fractions to fractions,

= $\frac{7}{10} \div \frac{3}{7}$ of $\left(\frac{23}{10}+\frac{13}{5}\right)+\frac{1}{5} \div \frac{7}{5}-\frac{2}{7}$

Applying BODMAS, we get,

= $\frac{7}{10} \div \frac{3}{7}\ $ of $ (\frac{49}{10})+\frac{1}{5} \div \frac{7}{5}-\frac{2}{7}$

= $\frac{7}{10} \div (\frac{21}{10})+\frac{1}{7}-\frac{2}{7}$

= $\frac{1}{3}-\frac{1}{7}$

= $\frac{4}{21}$

Hence, the correct answer is $\frac{4}{21}$.

Q7. The value of

$51 \div\left\{25+(25\right.$ of $12 \div 30)-\left(5^4 \div 5\right.$ of 125$\left.)\right\}$ is:

1. $\frac{2}{3}$

2. $\frac{3}{2}$

3. $-\frac{2}{3}$

4. $-\frac{3}{2}$

Answer:

Given: $51\div\left\{25+(25\right.$ of $12 \div 30)-\left(5^4 \div 5\right.$ of 125$\left.)\right\}$

$= 51\div\left\{25+(300\right.$ $ \div 30)-\left(5^4 \div 5^4\right.$$\left.)\right\}$

$= 51÷[25+10-1]$

$= \frac{51}{34}$

$= \frac{3}{2}$

Hence, the correct answer is $\frac{3}{2}$.

Q8. The value of $3\frac{1}{2} - [2\frac{1}{4}+ 1\frac{1}{4} - \frac{1}{2}(1\frac{1}{2}-\frac{1}{3} -\frac{1}{6})]$ is:

1. $\frac{1}{2}$

2. $2\frac{1}{2}$

3. $3\frac{1}{2}$

4. $9\frac{1}{2}$

Answer:

Given: $3\frac{1}{2} - [2\frac{1}{4}+ 1\frac{1}{4} -\frac{1}{2}(1\frac{1}{2}-\frac{1}{3} -\frac{1}{6})]$

$=3\frac{1}{2} -[2\frac{1}{4}+ 1\frac{1}{4} - \frac{1}{2}(\frac{3}{2}-\frac{1}{2})]$

$=3\frac{1}{2} -[2\frac{1}{4}+ 1\frac{1}{4} - \frac{1}{2}\times 1]$

$=3\frac{1}{2} -[\frac{9}{4}+\frac{5}{4} - \frac{1}{2}]$

$=3\frac{1}{2} -[\frac{14}{4} - \frac{1}{2}]$

$=3\frac{1}{2} -[\frac{12}{4}]$

$=\frac{7}{2} -3$

$=\frac{1}{2}$

Hence, the correct answer is $\frac{1}{2}$.

Q9. Simplify: $\sqrt{\frac{4\frac{1}{7}-2\frac{1}{4}}{3\frac{1}{2}+1\frac{1}{7}}+\frac{2}{2+\frac{1}{2+\frac{1}{5-\frac{1}{5}}}}}$

1. 1

2. $\sqrt{\frac{265}{130}}$

3. 2

4. $\sqrt{\frac{159}{130}}$

Answer:

Given: $\sqrt{\frac{4\frac{1}{7}-2\frac{1}{4}}{3\frac{1}{2}+1\frac{1}{7}}+\frac{2}{2+\frac{1}{2+\frac{1}{5-\frac{1}{5}}}}}$

= $\sqrt{\frac{\frac{29}{7}-\frac{9}{4}}{\frac{7}{2}+\frac{8}{7}}+\frac{2}{2+\frac{1}{2+\frac{5}{24}}}}$

= $\sqrt{\frac{\frac{53}{28}}{\frac{65}{14}}+\frac{2}{2+\frac{24}{53}}}$

= $\sqrt{\frac{53}{130}+\frac{106}{130}}$

= $\sqrt{\frac{159}{130}}$

Hence, the correct answer is $\sqrt{\frac{159}{130}}$.

Q10. Simplify the following expression.

2 + (30 – 26)2 ÷ 8{3 – 2} × 0.5

1. 2

2. 1

3. 3

4. 0

Answer:

Given: 2 + (30 – 26)2 ÷ 8{3 – 2} × 0.5

= 2 + 42 ÷ 81 × 0.5

= 2 + 16 ÷ 8 × 0.5

= 2 + 2 × 0.5

= 2 + 1

= 3

Hence, the correct answer is Option (C), 3.