Cyclic Quadrilateral and Geometric Centres of a Triangle: Meaning, Formula

Cyclic quadrilateral is a very important topic in Geometry. A cyclic quadrilateral is a four-sided polygon inside a circle and all of its vertices touch the circle. That circle is called a circumcircle. The cyclic quadrilateral properties include sum of the each pair of opposite angles must be 180 degrees. cyclic quadrilateral formula involves the area covered by the cyclic quadrilateral, its radius and diagonals.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

cyclic quadrilateral opposite angles are supplementary.

We will also discuss “cyclic quadrilateral examples”, “cyclic quadrilateral properties”,properties related to cyclic quadrilateral opposite angles”, “cyclic quadrilateral meaning”, “geometric centre of a triangle”, “geometry centroid of a triangle”, “cyclic quadrilateral area formula”, “cyclic quadrilateral class 10 chapters”, etc.

What is a Cyclic Quadrilateral?

A four-sided polygon whose all four vertices lie on the circumference of a single circle is called a Cyclic quadrilateral. That single circle is called a Circumcircle. Vertices are called concyclic. The centre of the circle is known as circumcentre and the radius of that circle is called circumradius.

The sum of opposite angles of cyclic quadrilaterals is always supplementary(that means their sum is 180 degrees).

Examples: Rectangles and Squares inscribed in a circle

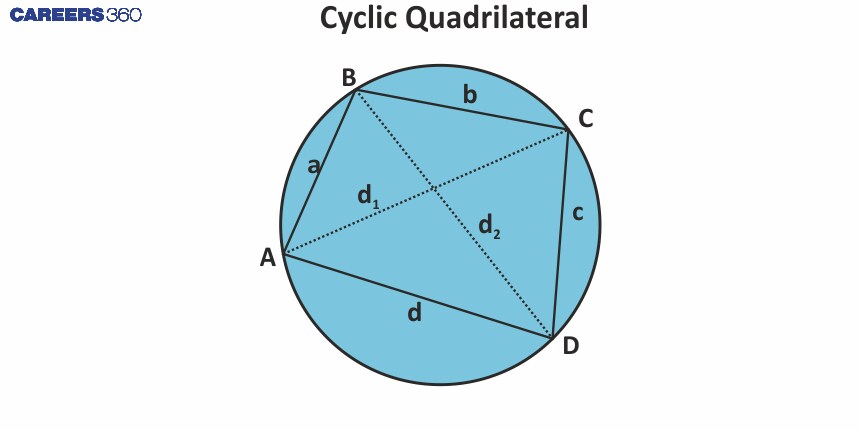
In the picture below, ABCD is a cyclic quadrilateral with side lengths a, b, c, and d and the circle is called a Circumcircle. O is the circumcentre. d1 and d2 are its diagonals.

Condition of a Quadrilateral to be a Cyclic Quadrilateral

There are several conditions for a quadrilateral to be cyclic. Those are:

• The sum of each pair of opposite angles must be 180 degrees. These angles are supplementary.

This is the most fundamental condition to be a cyclic quadrilateral.

• All four vertices of the quadrilateral must touch the circumference of a single circle.

• In cyclic quadrilaterals, the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals.

• The perpendicular bisectors of a cyclic quadrilateral are always concurrent.

Properties of a Cyclic Quadrilateral

Radius and diagonal of a cyclic quadrilateral

Radius of a Cyclic Quadrilateral

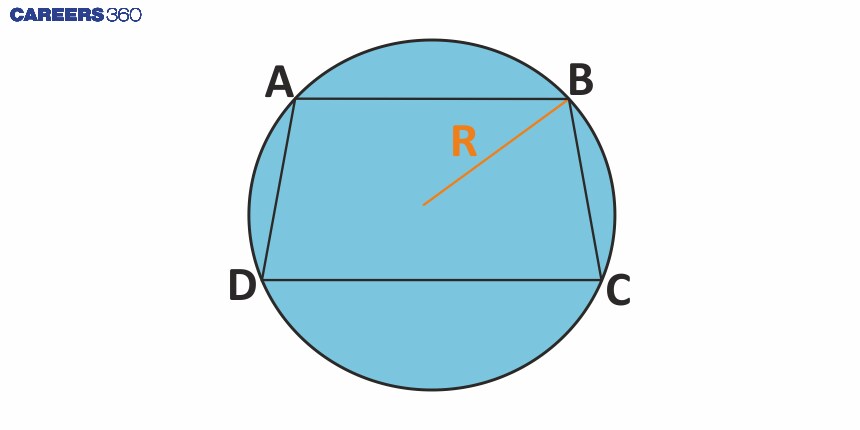
Let ABCD be a cyclic quadrilateral with AC and BD as its diagonals.

Let the lengths of AB, BC, CD and DA be a, b, c, and d, respectively.

R is the circumradius of the quadrilateral.

Semiperimeter, s = $\frac{a+b+c+d}{2}$

The formula to find the circumradius is:

R = $\frac{1}{4} \sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{(s-a)(s-b)(s-c)(s-d)}}$

Diagonals of a Cyclic Quadrilateral:

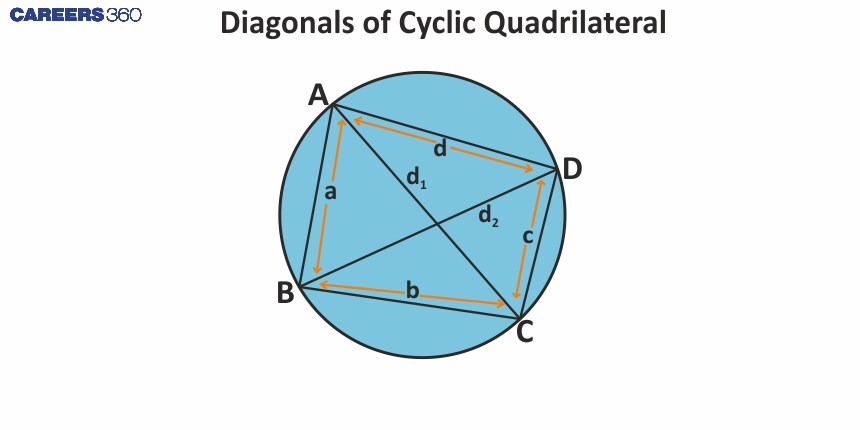
Let ABCD be a cyclic quadrilateral with AC and BD as its diagonals.

Let the lengths of AB, BC, CD and DA be a, b, c, and d, respectively.

Also, the length of AC and BD be d1 and d2, respectively.

So, the formula to find d1 and d2 is:

d1 = $\sqrt{\frac{(ac+bd)(ad+bc)}{ab+cd}}$

d2 = $\sqrt{\frac{(ac+bd)(ab+cd)}{ad+bc}}$

Area of a cyclic quadrilateral: Brahmgupta formula

To find the area of a Cyclic quadrilateral, we use Brahmagupta’s theorem.

Brahmagupta’s theorem states that the area of a cyclic quadrilateral ABCD with side length a, b, c, and d is: $\sqrt{(s-a)(s-b)(s-c)(s-d)}$, where s is the semiperimeter of the quadrilateral and calculated by s = $\frac{a+b+c+d}{2}$

Theorem of Cyclic quadrilateral

There are many important theorems on cyclic quadrilaterals.

We have given the statements and proved them below.

Ptolemy's Theorem of Cyclic Quadrilateral

Ptolemy's theorem is an important part of geometry, especially in problems involving cyclic quadrilaterals, allowing for elegant solutions and deeper insights into the relationships between sides and diagonals.

Statement: In a cyclic quadrilateral, the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals.

Proof:

ABCD is a cyclic quadrilateral whose diagonals are AC and BD.

We have to prove that AB × DC + AD × BC = AC × BD

Draw a line from point A which touches diagonal BD in point E.

Consider ΔADE and ΔACB

• ∠DAE = ∠CAB

• ∠ADE = ∠ACB

By A-A(Angle-Angle) similarity, ΔADE and ΔACB are similar triangles.

So,

$\frac{AD}{DE}=\frac{AC}{BC}$

⇒ AD × BC = AC × DE - - - - - - -(1)

Consider ΔAEB and ΔADC

• ∠ACD = ∠ABD

• ∠DAC = ∠BAE

By A-A(Angle-Angle) similarity, ΔAEB and ΔADC are similar triangles.

So,

$\frac{AC}{DC}=\frac{AB}{BE}$

⇒ AB × DC = AC × BE - - - - - - - -(2)

Adding equation 1 and 2, we get,

AD × BC + AB × DC = AC × DE + AC × BE

⇒ AB × DC + AD × BC = AC(DE + BE)

⇒ AB × DC + AD × BC = AC × DE [∵ DE + BE = DE]

Hence, it is proven that AB × DC + AD × BC = AC × BD

This proves that in a cyclic quadrilateral, the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals.

Inscribed Angle Theorem

Statement: The measure of an inscribed angle is half the measure of the central angle that subtends the same arc.

Proof:

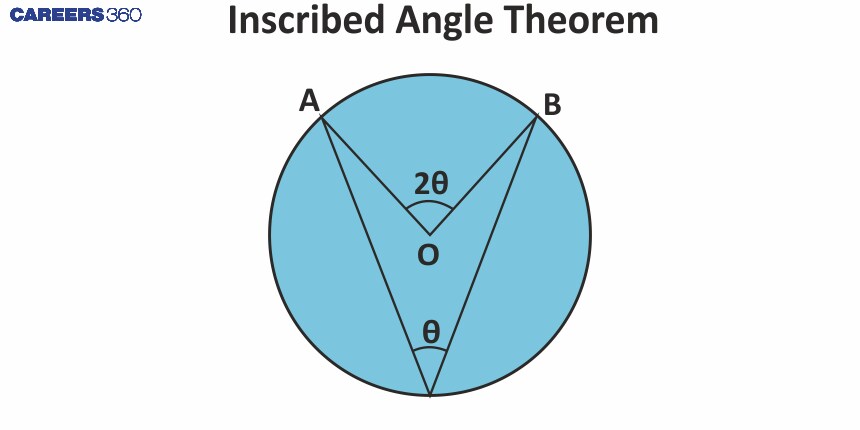
∠ACB is an inscribed angle angle in a circle and ∠AOB is a central angle subtended by the same arc AB,

We have to prove that: ∠ACB = $\frac{1}{2}$ × ∠AOB

We will consider three cases here.

• The centre of the circle lies on one side of the angle.

• The centre of the circle lies inside the angle.

• The centre of the circle lies outside the angle.

Case 1:

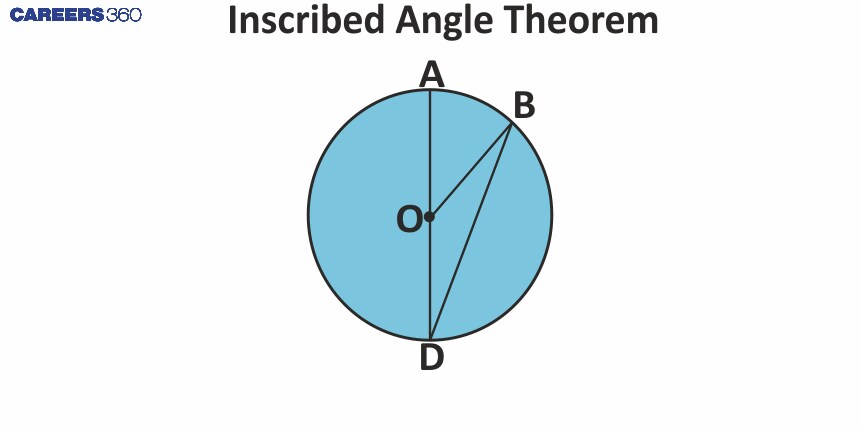
We have to prove that the $\frac{1}{2}$ ∠AOB = ∠ODB or, ∠OBD

Here, ΔBOD is an isosceles triangle as OD = OB (Radii of the same circle)

So, ∠ODB = ∠OBD

Let ∠ODB = ∠OBD = θ and ∠AOB = a

∠BOD = 180° - ∠AOB = 180° - a

According to the Angle sum property,

∠OBD + ∠ODB + ∠BOD = 180°

⇒ θ + θ + 180° - a = 180°

⇒ a = 2θ

Putting values, we get,

⇒ ∠AOB = 2∠ODB or, ∠AOB = 2∠OBD

⇒ $\frac{1}{2}$ ∠AOB = ∠ODB or, ∠OBD

Hence, it proved.

Case 2:

We have to prove, ∠ADB = $\frac{1}{2}$ × ∠ACB

Draw a diameter, that bisects both angles.

Let ∠ADB = θ

Also, θ = θ1 + θ2

Let ∠ACB = a

Also, a = a1 + a2

From case 1, we already know that,

a1 = 2θ1

and a2 = 2θ2

Adding both we get,

a1 + a2 = 2(θ1 + θ2)

⇒ a = 2θ

Putting values, we get,

⇒ ∠ACB = 2∠ADB

⇒ ∠ADB = $\frac{1}{2}$ × ∠ACB

Hence, proved.

Case 3:

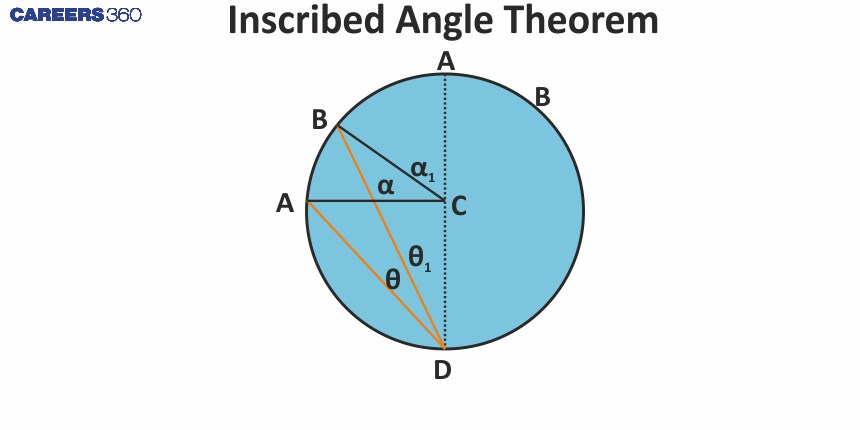
We have to prove, ∠ADB = $\frac{1}{2}$ × ∠ACB

Let ∠ADB = θ and ∠ACB = a

From case 2, we already know that a1 = 2θ1

a + a1 = 2(θ + θ1)

⇒ a + 2θ1 = 2θ + 2θ1

⇒ a = 2θ

⇒ ∠ACB = 2∠ADB

⇒ ∠ADB = $\frac{1}{2}$ × ∠ACB

Hence, it proved.

Geometrical centres of a cyclic quadrilateral

A cyclic quadrilateral has several important geometrical centres, each with distinct properties and significance. Here are the primary centres associated with a cyclic quadrilateral:

• Circumcentre

• Centroid

• Incentre

• Excentre

Important points

• The sum of the opposite angles of a cyclic quadrilateral is 180°.

• A cyclic quadrilateral's exterior angle is equal to its opposite interior angle.

• At any point on the circle, the diameter subtends a 90° angle.

• The two pairs of adjacent angles in a cyclic trapezium are equal in measure.

• The angle subtended by the chord at the centre is double that of the chord at the circumference.

• In cyclic quadrilaterals, the sum of the products of its two pairs of opposite sides is equal to the product of its diagonals.

Practice Questions

Q1. Three consecutive angles of a cyclic quadrilateral are in the ratio of 1 : 4 : 5. The measure of the fourth angle is:

1. 120°

2. 60°

3. 30

4. 80°

Hint: The sum of the opposite angles of a cyclic quadrilateral is 180°. Using this, find the measure of the fourth angle of the cyclic quadrilateral.

Answer:

Given: Three consecutive angles of a cyclic quadrilateral are in the ratio of 1 : 4 : 5.

We know that the sum of the opposite angles of a cyclic quadrilateral is 180°.

Let $\angle A=x°, \angle B=4x°,$ and $\angle C=5x°$.

Since $\angle A+ \angle C=180°$.

So, $x+5x=180°$

⇒ $6x=180°$

⇒ $x=30°$

Since $\angle B+ \angle D=180°$

So, $4x+\angle D=180°$

⇒ $4×30°+\angle D=180°$

⇒ $120°+\angle D=180°$

⇒ $\angle D=180°-120°$

⇒ $\angle D=60°$

So, the measure of the fourth angle is 60°.

Hence, the correct answer is 60°.

Q2. In a cyclic quadrilateral ABCD, the side AB is extended to a point X. If $\angle XBC=82°$ and $\angle ADB=47°$, then the value of $\angle BDC$ is:

1. 40°

2. 35°

3. 30°

4. 25°

Hint: A cyclic quadrilateral's exterior angle equals its opposite interior angle.

Answer:

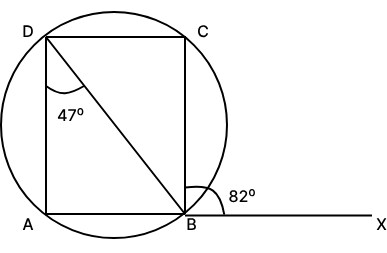
Given: In a cyclic quadrilateral ABCD, $\angle XBC=82°$ and $\angle ADB=47°$.

A cyclic quadrilateral's exterior angle is equal to its opposite interior angle.

So, $\angle XBC= \angle ADC=82°$.

Also, $\angle ADB=47°$

⇒ $\angle BDC=82°-47°$

⇒ $\angle BDC=35°$

Hence, the correct answer is 35°.

Q3. PQRS is a cyclic quadrilateral and PQ is the diameter of the circle. If $\angle RPQ=38°$, what is the value (in degree) of $\angle PSR$?

1. 52°

2. 77°

3. 128°

4. 142°

Hint: The sum of the opposite angles of a cyclic quadrilateral is 180°. Also, the sum of all the angles in the triangle is 180°. At any point on the circle, the diameter subtends a 90° angle.

Answer:

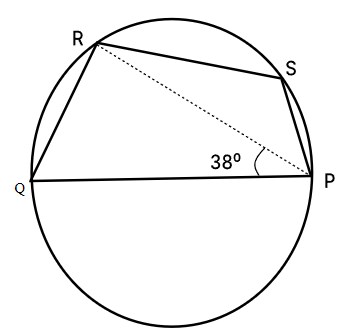
Given: PQRS is cyclic quadrilateral and PQ is the diameter of the circle and $\angle RPQ=38°$.

We know that the sum of the opposite angles of a cyclic quadrilateral is 180°. Also, the sum of all the angles in the triangle is 180°. Also, at any point on the circle, the diameter subtends a 90° angle.

Since PQ is the diameter of the circle. So, $\angle QRP=90°$.(Angle subtended by the diameter)

In $\triangle PRQ$,

$\angle RPQ+\angle PQR+\angle QRP=180°$

⇒ $\angle PQR=180°-90°-38°$

⇒ $\angle PQR=52°$

Since PQRS is a cyclic quadrilateral.

So, $\angle PQR+\angle PSR=180°$

⇒ $\angle PSR=180°-52°$

⇒ $\angle PSR=128°$

Hence, the correct answer is 128°.

Q4. The length of a side of a square inscribed in a circle is $a\sqrt2$ units. The circumference of the circle is:

1. $2\pi a$ units

2. $\pi a$ units

3. $4\pi a$ units

4. $\frac{2a}{\pi}$ units

Hint: The diameter of the circle will be equal to the length of the diagonal of the square.

Length of the diagonal = $\sqrt2\times$ side and circumference of the circle = $\pi d$, where $d$ is the length of the diameter.

Answer:

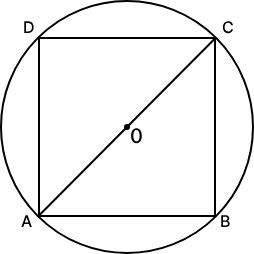
Given, Side of a square = AB = $\sqrt2 a$ units

We know, the length of the diagonal of a square = $\sqrt2\times$ side

⇒ AC = Diagonal = $\sqrt2 × \sqrt2 a=2a$ units = Diameter of the circle, $d$

$\therefore$ Circumference of circle = $\pi × d$ = $\pi × 2 a$ = $2π a$ units

Hence, the correct answer is $2\pi a$ units.

Q5. ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If $\angle$ABC = $75^{\circ}$, then the measure of $\angle$BCD is:

1. 75°

2. 95°

3. 45°

4. 105°

Hint: The two pairs of adjacent angles in a cyclic trapezium are equal in measure.

Answer:

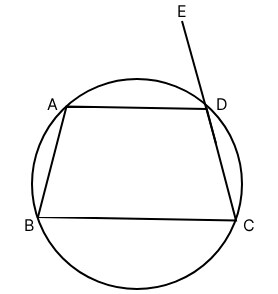
ABCD is a cyclic trapezium,

The two pairs of adjacent angles in a cyclic trapezium are equal in measure.

So, $\angle$ABC = $\angle$BCD = $75^{\circ}$.

Hence, the correct answer is $75^{\circ}$.

Q6. In the given figure, O is the centre of the circle, $\angle PQR=100^{\circ}$ and $\angle STR=105^{\circ}$. What is the value (in degree) of $\angle OSP$?

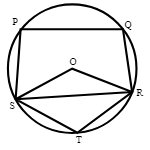
1. 95°

2. 45°

3. 75°

4. 65°

Hint: The angle subtended by the chord at the centre is double the angle subtended by the chord at the circumference. Also, opposite angles of a cyclic quadrilateral are supplementary.

Answer:

Given, $\angle PQR=100^{\circ}$ and $\angle STR=105^{\circ}$

Since the angle subtended by the chord at the centre is double the angle subtended by the chord at the circumference,

reflex$\angle SOR = 2\angle STR = 210^\circ$

So, $\angle SOR = 360^\circ-210^\circ = 150^\circ$

By angle sum property in $\triangle SOR$,

$\angle SOR + \angle OSR+ \angle ORS =180^\circ$

⇒ $150^\circ+ 2\angle OSR =180^\circ$

⇒ $\angle OSR = 15^\circ$

Since PQRS is a cyclic quadrilateral,

$\angle PSR=180^\circ - \angle PQR$

⇒ $\angle PSR=180^\circ - 100^\circ $

⇒ $\angle PSR=80^\circ$

$\angle OSP = \angle PSR - \angle OSR$

⇒ $\angle OSP = 80^\circ - 15^\circ$

⇒ $\angle OSP = 65^\circ$

Hence, the correct answer is 65.

Q7. AB is the diameter of a circle having a centre at O. PQ is a chord that does not intersect AB. Join AP and BQ. If $\angle$BAP = $\angle$ABQ, then ABQP is a:

1. cyclic square

2. cyclic trapezium

3. cyclic rhombus

4. cyclic rectangle

Hint: Draw the figure using the given data to solve this.

Answer:

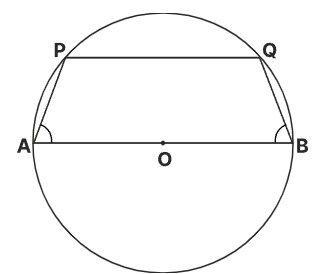
$\angle$BAP = $\angle$ABQ and AB $\neq$ PQ

Now, $\angle$BAP + $\angle$BQP = 180°

⇒ $\angle$ABQ + $\angle$BQP = 180°

⇒ AB || PQ

So, ABQP is a cyclic trapezium.

Hence, the correct answer is cyclic trapezium.

Q8. JKLM is a cyclic quadrilateral in which $\angle \mathrm{K}$ is opposite to $\angle \mathrm{M}$. When $\mathrm{JK}$ and $\mathrm{ML}$ are produced, meet at point $\mathrm{Z}$. $\mathrm{JK}=10 \mathrm{~cm}, \mathrm{KZ}=12 \mathrm{~cm}$ and $\mathrm{MZ}=33 \mathrm{~cm}$. What is the length of $\mathrm{LZ}$?

1. 9 cm

2. 8 cm

3. 10 cm

4. 12 cm

Hint: If chords AB and CD of a circle intersect each other at a point P outside the circle then,

PA × PB = PC × PD.Use this information to solve this problem.

Answer:

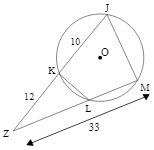
JKLM is a cyclic quadrilateral in which $\angle$K is opposite to $\angle$M.

When JK and ML are produced, meet at point Z.

JK = 10 cm, KZ = 12 cm, and MZ = 33 cm.

If chords AB and CD of a circle intersect each other at a point P outside the circle then,

PA × PB = PC × PD

Here,

ZK × ZJ = ZL × ZM

⇒ ZL = $12 \times \frac{22}{33}$

⇒ ZL = 8 cm

Hence, the correct answer is 8 cm.