Geometric Progression (G.P.) - Definition, Properties, Formulas & Examples

A geometric progression is a powerful mathematical concept with numerous applications in finance, biology, physics, and computer science. It is also called Geometric sequence. One of the most frequently used occasions of Geometric progression examples in real life is compound interest.

The formula to find the total amount after compound interest is:

Total amount = Principal( 1 + Rate)^Time, here rate is expressed as a decimal

Here, we can see the investment growing in a geometric progression where each year's amount is the previous year's amount multiplied by 1 + r.

In this article, we will learn more about Geometric progression, also we will learn the geometric progression formula, the sum of geometric progression, the formula of geometric progression, and the geometric progression calculator.

We will discuss what the geometric progression sum formula is and give a full explanation of the formula for geometric progression.

What is geometric Progression?

A Geometric progression or Geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio. It will be constant throughout the progression.

If we consider “a” as the first term, “r” as the common ratio, and “n” be the number of terms, then a, ar, ar², ar³, ar⁴, ar⁵,.......ar^n-1 is a Geometric sequence.

We can see that each term is multiplied by the common ratio “r” by its preceding term.

Comparison with Arithmetic Progression

Comparison with Harmonic Progression

Terms and Notations Used in Geometric Progression:

There are several key terms and notations used in Geometric Progression like first term(a), common ratio(r), number of terms(n), nth term of the progression(an), and sum of first n terms(s_n).

Now we will explain these terms.

First term (a):

As the name implies, it is the first or starting term of the progression. It is generally denoted by “a”.

Example: In the Geometric sequence 2, 4, 8, 16, and 32, 2 is the first term.

Common ratio (r):

The constant factor by which each term of the Geometric sequence is multiplied to get the next term is called the Common ratio. It will be constant throughout the whole sequence. It is generally denoted by "r".

If we divide the 2nd term by the 1st term, we will get the common ratio. It can be found by dividing any term by its preceding term.

Example: In the Geometric sequence 2, 4, 8, 16, and 32, 2 is the common ratio as $\frac{4}{2}=2$ or, $\frac{8}{4}=2$

Number of terms (n):

The number of terms in a finite geometric sequence is called the number. We denote it by “n”.
In an infinite series, there is no countable number of terms as it continues indefinitely.

Example: In the Geometric sequence 2, 4, 8, 16, and 32, there are 5 terms. It is a finite geometric sequence as we can count the number of terms.

The general term of a GP:

The terms of a Geometric progression are given by:

a, ar, ar², ar³, ar⁴,....... ar^n-1

Here, a is the first term of Geometric progression.

r is the common ratio.

ar^n-1 is the nth term of the geometric progression.

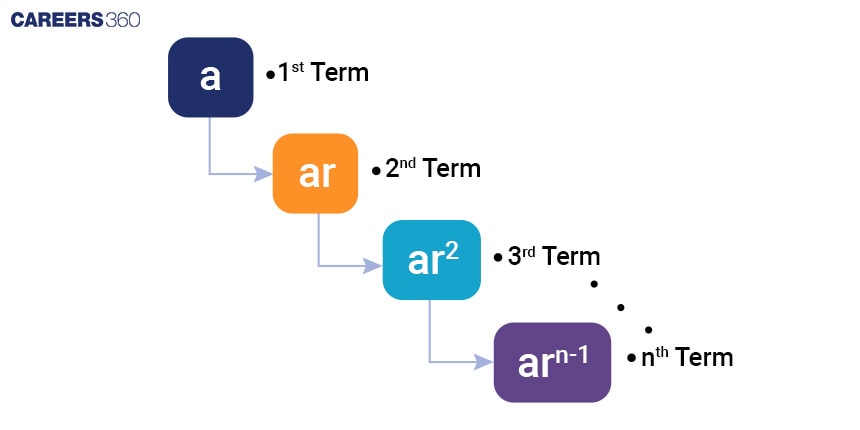
nth term of a GP:

If in a Geometric progression, “a” is the first term and “r” is the common ratio, then the nth term, an of that sequence is: a_n = ar^n-1 (as we can see in the image above)

Example: In a finite geometric sequence of 8 numbers, the first term is 4 and the common ratio is 2, then the 8th term, a₈ = 4 × 28-1 = 4 × 2⁷ = 4 × 128 = 512

Relating any two terms of a GP

Suppose a, ar, ar², ar³, ar⁴,....... arn-1 is a Geometric progression, where a is the first term, r is the common ratio and n is the number of terms.

Here, the ratio of any term with its preceding term will be equal throughout the sequence. That is called the common ratio.

$\frac{ar}{a}=\frac{ar^2}{ar}=\frac{ar^3}{ar^2}=\frac{ar^4}{ar^3}=.........\frac{ar^{n-1}}{ar^{n-2}}=r$

Example: 2, 4, 8, 16, and 32 are in Geometric progression.

Then, $\frac{4}{2}=\frac84=\frac{16}{8}=\frac{32}{16}=2$

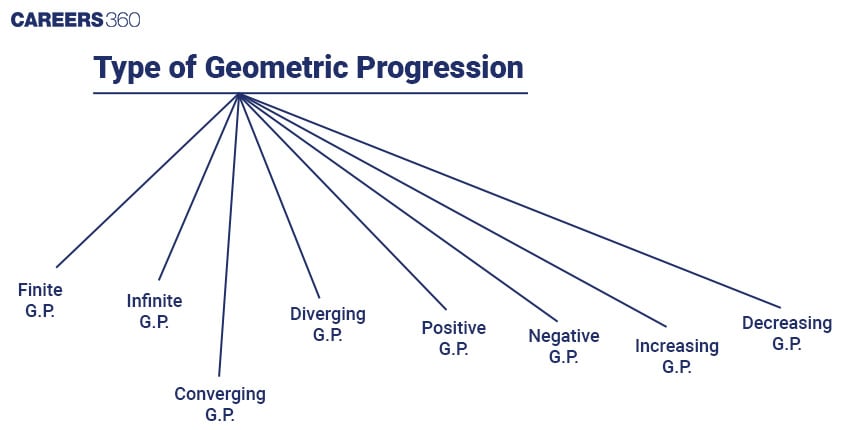
Types of Geometric Progression

Geometric progression can be classified into various types based on their property and the nature of the terms.

Some of the important types of Geometric progressions are:

1. Finite Geometric progression

2. Infinite Geometric progression

3. Diverging Geometric progression

4. Converging Geometric progression

5. Positive Geometric progression

6. Negative Geometric progression

7. Increasing Geometric progression

8. Decreasing Progression

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. What is geometric Progression?
2. Terms and Notations Used in Geometric Progression:
3. The general term of a GP:
4. Types of Geometric Progression
5. The sum of n terms of a GP
6. List of Geometric Progression formulae
7. Geometric Mean
8. Properties of Geometric Progression
9. Tips and Tricks
10. Solved Examples:

We have discussed these types of geometric progressions below in detail with examples.

Finite GP

If the number of terms in a Geometric sequence can be counted, then it is called a Finite Geometric Progression.

Example: In the Geometric sequence 2, 4, 8, 16, and 32, there are 5 terms. So this is a Finite Geometric progression.

Infinite GP

If the number of terms in a Geometric sequence can be counted as it continues indefinitely, then it is called Infinite Geometric Progression.

Example: In the Geometric sequence 2, 4, 8, 16, 32, ……., 2 is the first term, but there is no last term, so cannot count the exact number of terms in that sequence. So this is an Infinite Geometric progression.

Increasing and Decreasing GP

If in a Geometric sequence, the value of the common ratio is greater than 1, then terms in the Geometric sequence will be greater than the previous term. It is called Increasing Geometric Progression.

Example: In the Geometric sequence, 2, 4, 8, 16, and 32, we can see numbers are gradually increasing as the common ratio is 2 which is greater than 1.

If in a Geometric sequence, the value of the common ratio is between 0 and 1, then terms in the Geometric sequence will be smaller than the previous term. It is called Decreasing Geometric Progression.

Example: In the Geometric sequence, 100, 50, 25, 12.5, and 6.25, we can see the numbers are gradually decreasing as the common ratio is $\frac{1}{2}$ or 0.5 which is between 0 and 1.

Positive and Negative GP

If the first term and common ratio are positive in a Geometric progression, then all the terms of that progression will be positive. It is called a Positive Geometric Progression.

Example: In the Geometric sequence, 2, 4, 8, 16, and 32, the common ratio is 2 and the first term is 2. Both are positive numbers. So this is a positive Geometric progression as there are no negative terms in the sequence.

If the first term or common ratio of a Geometric progression is negative, then there will be at least 1 negative term in that sequence. It is called Negative Geometric Progression.

Example: In the Geometric sequence, 4,- 8, 16, -32, and 64, the common ratio is -2 and the first term is 4.

Here the common ratio is negative. So alternate numbers in this sequence are also negative. This is a negative Geometric progression.

Converging and Diverging GP

Geometric Progression can be converging or diverging depending on the value of the common ratio,r.

If the terms of a Geometric progression tend towards zero, then it is called a Converging Geometric sequence. Here the common ratio will be less than 1.

Example: In the Geometric sequence, $5, \frac{5}{3}, \frac{5}{9}, \frac{5}{27}$, numbers are moving towards zero. So this is a Converging Geometric progression.

If the terms of a Geometric progression tend towards infinity and move away from zero, then it is called a Diverging Geometric sequence. Here the common ratio will be greater than 1.

Example: In the Geometric sequence, 2, 4, 8, 16, and 32, numbers are moving away from zero. So this is a Diverging Geometric sequence.

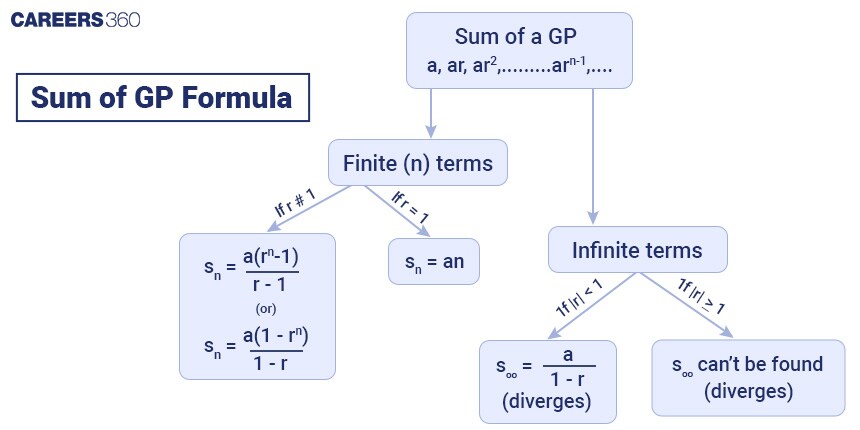
The sum of n terms of a GP

Suppose a, ar, ar², ar³, ar⁴,....... ar^n-1 is a Geometric progression, where a is the first term, r is the common ratio and n is the number of terms.

Then, the sum of the terms, sn = a + ar + ar² + ar³ + ar⁴ +....... + ar^n-1---------(1)

Let’s simplify this formula.

Multiply both sides by r, we get, rsn = ar + ar² + ar³ + ar⁴ +....... + arⁿ ---------(2)

Now, subtracting equation 1 from equation 2, we get,

r s_n - s_n = (ar + ar² + ar³ + ar⁴ +....... + arⁿ) - (a + ar + ar² + ar³ + ar⁴ +....... + ar^n-1)

⇒ s_n(r - 1) = ar^{n - a}

⇒ sn = $\frac{a(r^n-1)}{r-1}$

if r > 1

Sum of n terms, s_n = $\frac{a(r^n-1)}{r-1}$

This formula is true for r > 1

if r < 1

If r < 1, the formula becomes

s_n = $\frac{a(1-r^n)}{1-r}$

If r = 1

When r = 1, the formula of the sum of n terms becomes:

s_n = na

For infinite GP

Suppose a, ar, ar², ar³, ar⁴,....... is an Infinite Geometric progression, where a is the first term, r is the common ratio.

Then, the sum of the terms, s∞ = a + ar + ar² + ar³ + ar⁴ +.......---------(1)

Let’s simplify this formula.

Multiply both sides by r, we get, r s∞= ar + ar² + ar³ + ar⁴ +....... ---------(2)

Now, subtracting equation 2 from equation 1, we get,

s∞ - rs∞ = (a + ar + ar² + ar³ + ar⁴ +.......) - (ar + ar² + ar³ + ar⁴ +.......)

⇒ s∞(1 - r) = a

⇒ s∞ = $\frac{a}{1-r}$

This is true for $\left | r \right | < 1$.

If the value of $\left | r \right | \geq 1$, the terms of the sequence diverge towards infinity and cannot have a sum.

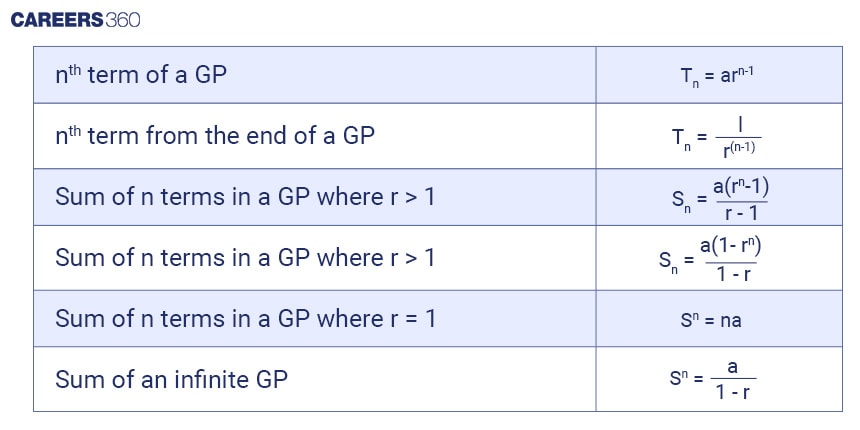
List of Geometric Progression formulae

The general term of Geometric progression is given by:

a, ar, ar², ar³, ar⁴,....... ar^n-1

Here, a is the first term of Geometric progression.

r is the common ratio.

l is the last term of a geometric progression

arn-1 is the nth term of the geometric progression.

Geometric Mean

In mathematics, the term mean is defined as the average of the given number of values.

Generally, we get the mean of the numbers by dividing the sum of the numbers by the count of the number.

However, to find the geometric mean, we have to multiply the numbers and then take the root of the corresponding count of numbers.

To understand the central tendency of sets of numbers that are multiplicative, Geometric mean is very useful.

Formula to find the Geometric Mean:

For a set of n positive integers a₁, a₂, a₃, a₄, .........a_n

Geometric mean = $\sqrt[n]{a_1× a_2× a_3× a_4× .......× a_n}$

Example: Geometric mean of 2, 4, 8, and 16 = $\sqrt[4]{2×4×8×16}=\sqrt[4]{1024}=5.66$

To know more about Geometric Mean, Click here.

Properties of Geometric Progression

• Three non-zero numbers a, b, and c can be in Geometric progression if b² = ac

Example: 2, 4, and 8 are in Geometric progression as 4² = 2 × 8

• The common ratio throughout a Geometric sequence will always be constant.

• If we multiply or divide all the terms of a geometric progression by a non-zero constant, then the resultant sequence will always be in Geometric progression with the same common ratio.

Example: 4, 8, 16, 32, and 64 are in Geometric progression with a common ratio of 2.

If we divide the sequence by 2, then the new sequence becomes 2, 4, 8, 16, 32, which is also in Geometric progression with the same common ratio of 2.

• If the common ratio is negative, then terms of that geometric progression will alternate in signs.

Example: 4, -8, 16, and -32 are in Geometric progression with common ratio -2.

• If we raise the power of all the terms of a geometric progression by a non-zero constant, then the resultant sequence will always be in Geometric progression.

Example: 4, 8, 16, 32, and 64 are in Geometric progression.

If square, every term of this sequence, i.e., 16, 64, 256, 1024, and 4096, is also in Geometric progression.

• In a finite geometric progression, the product of terms equidistant from the ends is constant and equal to the product of the first and last terms.

Example: Suppose a, ar, ar², ar³, ar⁴,....... ar^n-1 is a Geometric progression, where a is the first term, r is the common ratio and n is the number of terms.

Then, a × ar^n-1 = ar × ar^n-2 = ar² × ar^n-3 and so on

• If we take the logarithm of each term in a Geometric progression, then the sequence will turn into an Arithmetic progression and vice versa.

Example: 2, 4, 8, 16, and 32 is a Geometric sequence.

Taking the logarithm of each term in this sequence, we get,

log₂ 2, log₂ 4, log₂ 8, log₂ 16, log₂ 32

= 1, 2, 3, 4, 5 which are in Arithmetic progression

Tips and Tricks

• To check if a sequence is in Geometric progression, we can check if the ratio of consecutive terms is constant. If it is constant, then the sequence is in Geometric progression.

• The formula to the nth digit of the sequence is: an = arn-1, Where a = first term, r = common ratio, and n = number of terms

• The sum of the first n terms of the Geometric sequence, sn = $\frac{a(r^n-1)}{r-1}$ if $r \neq 1$

• The sum of the first n terms of the Geometric sequence, sn = na if $r = 1$

• Three non-zero numbers a, b, and c can be in Geometric progression if b2 = ac

Solved Examples:

Q1. Find the sum of 3 + 32 + 33 + ... + 38.

1. 3280

2. 6561

3. 6560

4. 9840

Hint: Use the following formula to solve this problem.

The sum of a Geometric progression of $n$ terms with first term $a$ and common ratio equal to $r$ = $\frac{a\times{(r^{n}-1)}}{r-1}$

Answer:

The given sequence represents GP of constant ratio $r$ = 3,

The sum of a Geometric progression (GP) of $n$ terms with first term $a$ and common ratio equal to $r$ = $\frac{a\times{(r^{n}-1)}}{r-1}$

According to the question $n = 8, a = 3$

$\therefore$ Sum = $\frac{3\times{(3^{8}-1)}}{3-1}$ = 9840.

Hence the correct answer is 9840.

Q2. The least value of n, such that (1 + 3 + 32+.......+3n) exceeds 2000, is:

1. 3

2. 7

3. 5

4. 8

Hint: Use the formula: Sn = $\frac{ar^n–1}{r-1}$ for the series a + ar + ar² +.......+ ar^n–1.

Answer:

Series = 1 + 3 + 3² + ...+ 3ⁿ

It is a geometric series whose common ratio is 3.

We know,

a + ar + ar²+.......+ar^n–1 = $\frac{ar^n–1}{r-1}$, where r >1

Here, a = 1, r = 3

Using the formula: Sn = $\frac{1(3^{n+1}-1)}{3-1}$

According to the question,

$\frac{3^{n+1}-1}{3-1}$ > 2000

⇒ $3^{n+1}-1$ > 4000

⇒ $3^{n+1}$ > 4001

For $n = 7$

38 = 6561 > 4001
The least value of n is 7 for which the sum of the sequence is greater than 2000.

Hence, the correct answer is 7.

Q3. Find the $n$th term of the following sequence: 5 + 55 + 555 + ........+ $T_n$

1. $5(10^n-1)$

2. $5^n(10^n-1)$

3. $\frac{5}{9}(10^{n} - 1)$

4. $(\frac{5}{9})^{n} (10^{n} -1)$

Hint: The nth term of a GP = $ar^{n-1}$ where a is the first term of GP and $r$ is the common ratio.

Answer:

Given: 5 + 55 + 555 + ........

$n$th term = 5 (1 + 11 + 111 + ... to $n$ terms)

Multiplying and divide by 9 in series,

$n$th term = $\frac{5}{9}$(9 + 99 + 999 +... to $n$ terms)

⇒ $n$th term = $\frac{5}{9}$[(10–1) + (102 –1) +...+ $(10^{n} -1)$]

⇒ $n$th term = $\frac{5}{9}(10^{n} –1)$

Hence, the correct answer is $\frac{5}{9}(10^{n} - 1)$.

Q4. The average of $n$ numbers is $a$. The first number is increased by 2, the second one is increased by 4, the third one is increased by 8, and so on. The average of the new numbers is:

1. $a+\frac{2^{n–1}–1}{n}$

2. $a+\frac{2(2n–1)}{n}$

3. $a+\frac{2^{n–1}}{n}$

4. $a+\frac{2^{n}–1}{n}$

Hint:

The sum of n terms of geometric series = $\frac{a(r^{n}–1)}{r–1}$, where $a$ is the first term and $r$ is the common ratio.

Answer:

Given: The average of $n$ numbers is $a$.

The sum of $n$ numbers is $n×a$.

According to the question,

Let S be the sum of increased value and $r$ = common ratio = $\frac{4}{2}= 2$

S = 2 + 4 + 8 + 16 .... upto $n$ terms.

It is a geometric series.

S = $\frac{a(r^{n}–1)}{r–1}=\frac{2(2^{n}–1)}{2–1}= 2(2^{n}–1)$

Now, the sum of old numbers and increased value is $(n×a)+2(2^{n}–1)$.

So, the required average = $\frac{na+2(2^{n}–1)}{n}=a+\frac{2(2^{n}–1)}{n}$

Hence, the correct answer is $a+\frac{2(2^{n}–1)}{n}$.

Q5. If $A =(\frac{1}{0.4})+(\frac{1}{0.04})+(\frac{1}{0.004})+....$ upto 8 terms, then what is the value of $A$?

1. 27272727.5

2. 25252525.5

3. 27777777.5

4. 25555555.5

Hint: Write all terms as $(\frac{1}{0.4}) = (\frac{10}{4})$ and use the formula of the sum of Geometric progression, $S_n = \frac{a(r^n-1)}{r-1}$, when $r>1$, where $a$ = first term, $r$ = common ratio, $n$ = number of terms

Answer:

Given: $ A =(\frac{1}{0.4})+(\frac{1}{0.04})+(\frac{1}{0.004})+....$ upto 8 terms.

This expression can be written as:

$⇒ A =(\frac{10}{4})+(\frac{100}{4})+(\frac{1000}{4})+(\frac{10000}{4})+(\frac{100000}{4})+(\frac{1000000}{4})(\frac{10000000}{4})+(\frac{100000000}{4})$

Using the formula, $S_n = \frac{a(r^n-1)}{r-1}$, where $a$ = first term, $r$ = common ratio, $n$ = number of terms

$10 + 100 + 1000+ .............+ 100000000 = \frac{10(10^8-1)}{10-1}=111111110$

$⇒ A=(\frac{111111110}{4})$

$\therefore A = 27777777.5$

Hence, the correct answer is 27777777.5.

Q6. Let $a_1, a_2, a_3, \ldots, a_{201}$ are in Geometric progression with $a_{101}=25$ and $\sum_{i=1}^{201} a_i=625$. Then the value of $\sum_{i=1}^{201} \frac{1}{a_i}$ equals:

1. 1

2. 25

3. $\frac{1}{25}$

4. $\frac{1}{625}$

Answer:

$\begin{aligned} \sum_{i=1}^{201} a_i=\frac{a\left(r^{201}-1\right)}{(r-1)}\ \text{and}\ \sum_{i=1}^{201} \frac{1}{a_i} & =\frac{1}{a} \frac{\left(r^{201}-1\right)}{(r-1)} \cdot \frac{1}{r^{200}} \\ \\& =\frac{1}{\left(a_{101}\right)^2} \cdot \sum_{i=1}^{201} a_i\end{aligned}$

$a_{101} = 25 \ \text{and} \ \sum_{i=1}^{201} a_i = 625 $

$\therefore \frac{1}{\left(a_{101}\right)^2} \cdot \sum_{i=1}^{201} a_i = \frac{ 625}{25^2} = 1$

Hence, the correct answer is 1.

Q7. If the sum and product of four positive consecutive terms of a G.P. are 126 and 1296, respectively,

then the sum of common ratios of all such GPs is:

1. 7

2. 3

3. 9

4. 14

Hint: Sun of n terms of GP, sn = $\frac{a(r^n-1)}{r-1}$

Answer:

Four terms of G.P. are $\frac{a}{r^{3}}\, ,\, \frac{a}{r},ar\, ,ar^{3}$.

$\begin{aligned} & \frac{a}{r^3}+\frac{a}{r}+a r+a r^3=126 ------(1)\\ & \frac{a}{r^3} \cdot \frac{a}{r} \cdot a r \cdot a r^3=1296 -----(2)\\ & ⇒a^4=1296 \\ &\therefore a=6 \\ & \text{Putting the value of a in equation(1), we get,}\\ &\frac{6}{r^3}+\frac{6}{r}+6 r+6 r^3=126 \end{aligned}$

$⇒(r+\frac{1}{r})+r^3+\frac{1}{r^3}=21$

$⇒(r+\frac{1}{r})+(r+\frac{1}{r})^3-3(r+\frac{1}{r})=21$

Let $(r+\frac{1}{r})=t$

So, $t^3-2t=21$

$⇒t=3$

Now, putting the value of t, we get,

$\begin{aligned} & r+\frac{1}{r}=3 \\ & ⇒r^2-3 r+1=0 \\ &⇒ r=\frac{3 \pm \sqrt{9-4}}{2} \\ &\therefore r=\frac{3 \pm \sqrt{5}}{2} \end{aligned}$

The sum of the common ratios = $\frac{9}{4}+\frac{5}{4}+\frac{3 \sqrt{5}}{2}+\frac{9}{4}+\frac{5}{4}-\frac{3 \sqrt{5}}{2}=7$

Hence, the correct answer is 7.

Q8. If a, b, and $\frac{1}{18}$ are in Geometric progression and $\frac{1}{a},10,$ and $\frac{1}{b}$ are in an arithmetic progression, then (16a + 12b) equals to: (a, and b are two positive integers)

1. 3

2. 5

3. 7

4. 9

Hint: If a, b, c are in A.P., then 2b = a + c

If a, b, c are in GP, then b2 = a.c

Answer:

$\begin{aligned} & \mathrm{b}^2=\frac{a}{18} ------(1)\\ & 20=\frac{1}{a}+\frac{1}{b}-----(2) \\ &⇒ a=\frac{b}{20 b-1} \\ & \text{Putting the value of a in equation 1, we get,} \\ & b^2=\frac{1}{18} \times \frac{b}{20 b-1} \\ &⇒ 360 b^2-18 b-1=0 \\ & ⇒360 b^2-30 b+12 b-1=0 \\ & ⇒(12 b-1)(30 \mathrm{~b}+1)=0 \\ &⇒ b=\frac{1}{12}, \frac{-1}{30}(\text { rejected }) \\ & \therefore a=\frac{1}{8} \\ & \text{So,}\ 16 \mathrm{a}+12\mathrm{b}=2+1=3 \end{aligned}$

Hence, the correct answer is 3.

Q9. Let the first term a and the common ratio r of a geometric progression be positive integers. If the sum of squares of its first three is 33033, then the sum of these terms is equal to:

1. 210

2. 220

3. 231

4. 241

Answer:

Let a, a^r, and ar² be three terms of GP.

$\mathrm{a}^2+\mathrm{(a r)}^2+\left(\mathrm{ar}^2\right)^2=33033$

$\begin{aligned} & a^2\left(1+r^2+r^4\right)=11^2 × 3×7×13 \\ & \text{Comparing both sides, we get, a = 11, and} \\ & 1+r^2+r^4=3×7×13 \\ & \Rightarrow r^2\left(1+r^2\right)=273-1 \\ & \Rightarrow r^2\left(r^2+1\right)=272=16 \times 17 \\ & \Rightarrow r^2\left(1+r^2\right)=4^2(4^2+1) \\ & \text{Comparing both sides, we get, r = 4} [\because r>0]\end{aligned}$

$\therefore$ Sum of these three terms = a + ar + ar2 = a(1 + r + r2 ) = 11(1 + 4 + 42) = 231

Hence, the correct answer is 231.

Q10. Consider two Geometric progressions 2, 22, 23, ..... and 4, 42, 43,..... of 60 and n terms, respectively.If the geometric mean of all the (60 + n) terms is $2^{\frac{225}{8}}$, then ${\sum_{k=1}^{n} \mathrm{k}(\mathrm{n}-\mathrm{k})}$ is equal to:

1. 560

2. 1540

3. 1330

4. 2600

Answer:

Given:

$\mathrm{\left(\left(2^{1} \cdot 2^{2} \cdot \cdots \cdot 2^{60}\right)\left(4^{1} \cdot 4^{2} \cdot \cdot \cdot 4^{n}\right)\right)^{\frac{1}{60+n}}=2^{\frac{225}{8}}}$

$⇒\mathrm{\left(2^{30 \times 61} \cdot 4^{\frac{n(n+1)}{2}}\right)^{\frac{1}{60+n}}=2^{\frac{225}{8}}}$

$⇒\mathrm{2^{1830+n^{2}+n}=2^{\frac{\left ( 225 \right )\left ( 60+n \right )}{8}}} \\$

$\Rightarrow \mathrm{8 n^{2}-217 n+1140=0} \\$

$\Rightarrow \mathrm{n=20,\frac{57}{8}} \\$

Now,

$\mathrm{\sum_{k=1}^{n} n k-k^{2}=\frac{n^{2}(n+1)}{2}-\frac{n(n+1)(2 n+1)}{6}}=1330$

Hence, the correct answer is 1330.