HCF and LCM - Definition, Formula, Full Form, Examples

A factor of a number is a divisor of the given number that divides it completely without leaving any remainder. A multiple of a number can be defined as a product of the given number and any other natural number. For example, factors of 10 are 1, 2, 5, 10, and multiples of 10 are 10, 20, 30, 40,…..etc.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. Definition of HCF and LCM
2. How to find the Highest Common Factor/Greatest Common Divisor:
3. Types of HCF Problems:
4. How to find the Least Common multiple:
5. Types of LCM Problems:
6. Relation between HCF and LCM and the two numbers:
7. Tips and Tricks to solve the questions of HCF and LCM:
8. Practice questions:

Understanding the terms multiples and factors is essential for a deeper understanding of the definitions of LCM and HCF.

HCF & LCM is a very common and important topic to solve problems related to Time, Speed and Distance, Time & Work etc.

The HCF is the highest common factor between two or more numbers. Whereas, the LCM is the lowest common multiple of two or more numbers which is exactly divisible by these numbers. HCF can also be called the Greatest Common Factor of two or more numbers.
The common questions that arise in a student’s mind while solving the problems of hcf & lcm, are ‘how do I find the least common multiple’, ‘how to calculate highest common factor’, ‘how to determine least common multiple’, ‘how to do highest common factor’, ‘what is the formula of hcf and lcm’, ‘how to find highest common factor’ etc.

In mathematics hcf and lcm play an important and crucial role. In this article, we are going to discuss the hcf lcm formula and also the hcf and lcm examples.

Definition of HCF and LCM

HCF Definition:

The greatest common divisor (GCD) or the highest common factor (HCF) of two or more numbers is the largest positive integer that divides the numbers without leaving a remainder.

For example, the HCF of 12 and 15 is 3 as it is the largest positive integer that can divide both 12 and 15 without leaving any remainder.

LCM Definition:

The least common multiple (LCM) of two or more numbers is the smallest or the least positive integer that is completely divisible by all of them. For example, the LCM of 6 and 8 is 24 as it is the least positive integer that is divisible by both 6 and 8.

How to find the Highest Common Factor/Greatest Common Divisor:

Understanding how to compute the HCF can greatly simplify mathematical problems and make complex calculations more manageable. There are several methods to find the HCF, each with its unique approach and advantages.

HCF of two or more integers:

Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two or more numbers can be done using various methods.

While finding hcf and lcm of two or more numbers, we should consider the following methods:

1. Calculating HCF by long division method:

When determining the HCF of large numbers, the long-division method works better. The following are the steps to be taken while using the long-division method:

• Step 1: First, divide the large number by the smaller number.

• Step 2: Then, set the remainder obtained as the new divisor and treat the previous divisor as the new dividend.

• Step 3: Next, divide the first divisor by the first remainder.

• Step 4: After that, divide the second divisor by the second remainder.

• Step 5: Keep doing this until the remainder becomes zero.

• Step 6: At last, the divisor, which does not leave a remainder, is the HCF of the two numbers, therefore, the last divisor is the required HCF of the given numbers.

Let's take an example to understand it more clearly.

Find the HCF of 120 and 192 using the long division method.

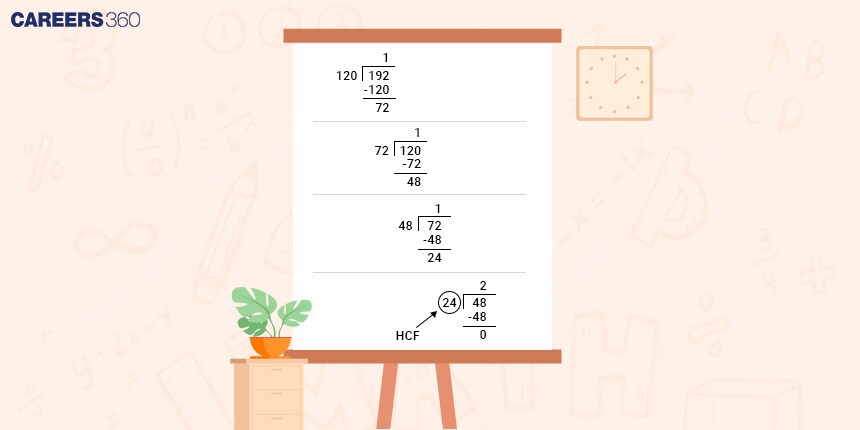
The last divisor is 24, so the HCF of 120 and 192 is 24.

2. Calculating HCF by Prime Factorisation method:

The prime factorisation method involves breaking down each number into prime factors and then identifying the common prime factors. Here’s a step-by-step guide for using this method:

• Step 1: Factorize each number into its prime factors.

• Step 2: List all the prime factors of each number.

• Step 3: Identify the common prime factors.

• Step 4: Take the lowest power of each common prime factor and multiply them to get the HCF.

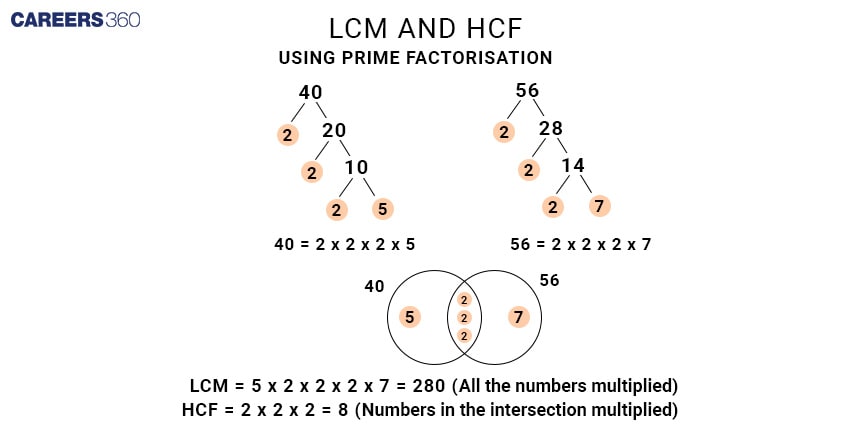
For example, let’s find the HCF of 36 and 60 using the prime factorization method.

Prime factorisation of 36 = $2^2 × 3^2$

Prime factorisation of 60 = $2^2 × 3 × 5$

So, the HCF is $2^2 × 3$ = 12.

3. Calculating HCF by Repeated Division method:

This method is somewhat similar to the long-division method. Let’s understand this with the following steps.

• Step 1: Divide the given numbers by the smallest common prime factor.

• Step 2: Divide the following quotients obtained, by their smallest common prime factor.

• Step 3: Repeat this process until there is no more common prime factor between the quotients.

• Step 4: Multiply all the divisors (prime factors) to get the required HCF.

For example, Let’s find the HCF of 72 and 96 using repeated division.

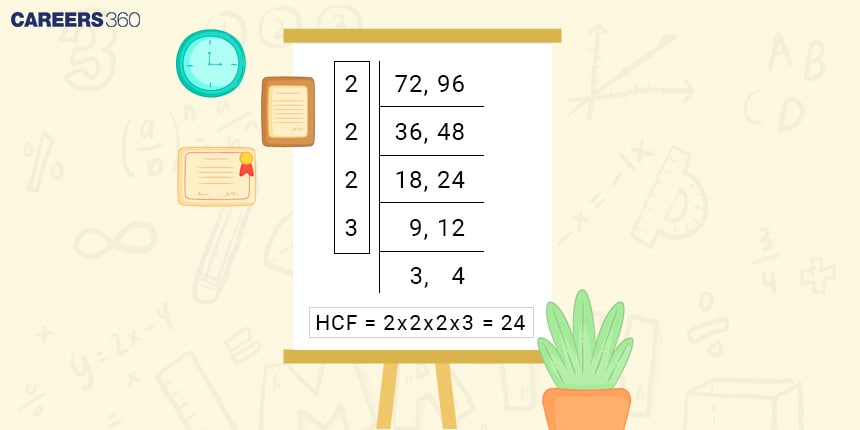
Therefore, the HCF of 72 and 96 is 24.

4. Calculating HCF by Euclid’s division algorithm:

This method is applicable only for positive integers and it is used to find HCF of two positive integers. According to Euclid’s division lemma, if we have two positive integers a and b (a>b), then there would be whole numbers q and r that satisfy the equation a = bq + r, where $0 \leq r < b$. Here’s a step-by-step guide for using this method:

• Step 1: we express the larger number “a” in terms of the smaller number “b” in the quotient remainder form a = bq + r

• Step 2: If r = 0, then b is the G.C.D. of a and b.

• Step 3: If $r \neq 0$, then we apply this process on b and r.

• Step 4: Continue the above process until the remainder is zero.

• Step 5: When the remainder is zero, the last divisor at this stage is the HCF of given numbers.

Let’s see an example: Find the G.C.D. of 1180 and 482.

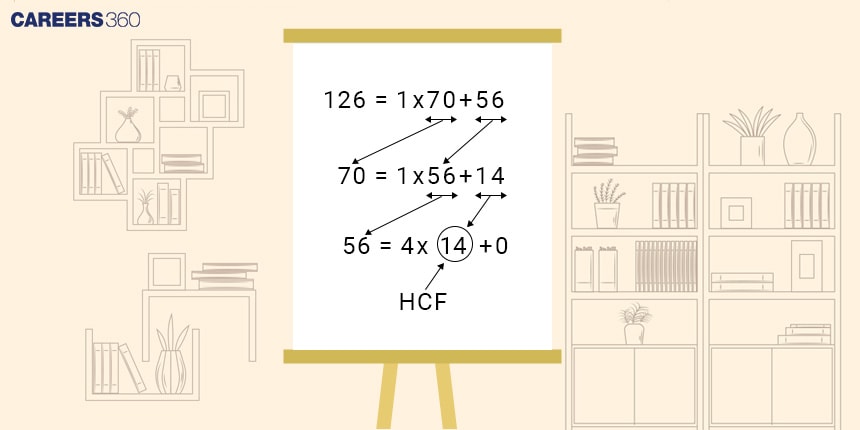
Therefore, the HCF of 1180 and 482 is 2.

Types of HCF Problems:

Problems on HCF can be divided into different categories as listed below:

1. HCF of two or more numbers if there is no remainder in each case:

If there is no remainder in each case then we can easily find the HCF of two more numbers using various methods such as prime factorisation, long division, repetitive division etc.

For example, find the greatest number which divides 18, 24, and 30 and leaves no remainder in each case.

Sol: We need to find the HCF of 18, 24, and 30 to get the required number.

18 = 2 × 3 × 3

24 = 2 × 2 × 2 × 3

30 = 2 × 3 × 5

So, the HCF of 18, 24, and 30 is 2 × 3 = 6.

Therefore, the greatest number which when divides 18, 24, and 30 and leaves no remainder in each case is 6.

2. HCF of two or more numbers if there is a remainder in each case (Remainder is known):

In case we need to find the HCF of two or more numbers where the remainder in each case is given, then we need to subtract those remainder from the respective numbers and calculate The HCF of those subtracted numbers to find the required HCF.

For example, Find the greatest number which when divides 127 and 191 leaves remainders 3 and 5, respectively.

Here, the numbers 127 and 191 leave the remainders 3 and 5 respectively. So, the required number will be obtained by finding the HCF of 127 – 3 = 124 and 191 – 5 = 186.

Now, 124 = 2 × 2 × 31 and 186 = 2 × 3 × 31

So, the HCF of 124 and 186 is (31 × 2) = 62

Therefore, the required number is 62.

3. HCF of two or more numbers if there is equal remainder in each case (Remainder is unknown):

Sometimes, in HCF problems the remainder is not given, generally, there will be three numbers given with equal remainder condition. To solve these types of problems we need to take the difference between the three pairs of numbers, now the HCF of these differences will become the required solution.

Let’s look at an example to understand this more clearly.

Find the greatest number, which when divided 67, 77, and 97 leaves the same remainder.

Let’s take the differences of three pairs of these numbers i.e. (77 - 67) = 10, (97 - 77) = 20, and (97 - 67) = 30.

Now, HCF of 10, 20, 30 is 10.

Therefore, the required number is 10.

4. HCF of two or more fractions:

To find the HCF of two or more fractions we use the formula below:

HCF of fraction = $\frac{\text{HCF of numerators}}{\text{LCM of denominators}}$

Example: Find the HCF of $\frac{4}{5}$ and $\frac{6}{7}$.

HCF of $\frac{4}{5}$ and $\frac{6}{7}$ = $\frac{\text{HCF of 4 and 6}}{\text{LCM of 5 and 7}}$

So, the required HCF of $\frac{4}{5}$ and $\frac{6}{7}$ is $\frac{2}{35}$.

Important properties of HCF:

• Property 1: HCF of any two or more numbers is never greater than any of the given numbers. For example, the HCF of 4 and 6 is 2, which is not greater than 4 or 6.

• Property 2: The HCF of co-prime numbers is always 1. For example, the HCF of 23 and 24 is 1.

• Property 3: The order of the numbers does not affect the HCF. Which means the HCF of a and b is the same as the HCF of b and a.

How to find the Least Common multiple:

Finding the lowest common multiple (LCM) of numbers is important in various mathematical problem-solving. Also finding the LCM is a valuable skill that applies to various practical and theoretical problems, making it an essential part of mathematics and its applications.

LCM of two or more integers:

LCM of numbers can be calculated using various methods. Let us see how to find the lowest common multiple (LCM) using the 3 methods given below.

1. Calculating LCM by Listing method:

We can find common multiples of two or more numbers by listing their multiples. Out of these common multiples, the least common multiple is the LCM of the given numbers.

For example, let’s find the LCM of 12 and 18 by the listing method.

Multiples of 12 = 12, 24, 36, 48, 60, 72, .....

Multiples of 18 = 18, 36, 54, 72, 90, .....

So, the common multiples are 36, 72, ….

Therefore, the least common multiple or the LCM of 12 and 18 is 36.

2. Calculating LCM by Prime Factorisation method:

To calculate the LCM of two numbers using the prime factorization method, we use the steps given below:

• Step 1: Factorize each number into its prime factors.

• Step 2: List all the prime factors of each number in their exponent form.

• Step 3: Find the product of only those prime factors that have the highest power.

• Step 4: The product is the required LCM of the numbers.

Example: Find the least common multiple (LCM) of 40 and 50 using prime factorisation.

Prime factorisation of 40 = 2 × 2 × 2 × 5 = $2^3 × 5$

Prime factorisation of 50 = 2 × 5 × 5 = $2 × 5^2$

So, the LCM of 40 and 50 is $2^3 × 5^2$ = 200.

3. Calculating LCM by Division method:

To calculate the LCM of two numbers using the prime factorization method, we use the steps given below:

• Step 1: First, write the numbers, separated by commas

• Step 2: Now divide the numbers, by the smallest prime number.

• Step 3: If any number is not divisible, then write down that number and proceed further

• Step 4: Keep on dividing the row of numbers by prime numbers, unless we get the results as 1 in the complete row

• Step 5: Now LCM of the numbers will be equal to the product of all the prime numbers we obtained in the division method

Example:

Find the LCM of 12, 15, and 18 using the division method.

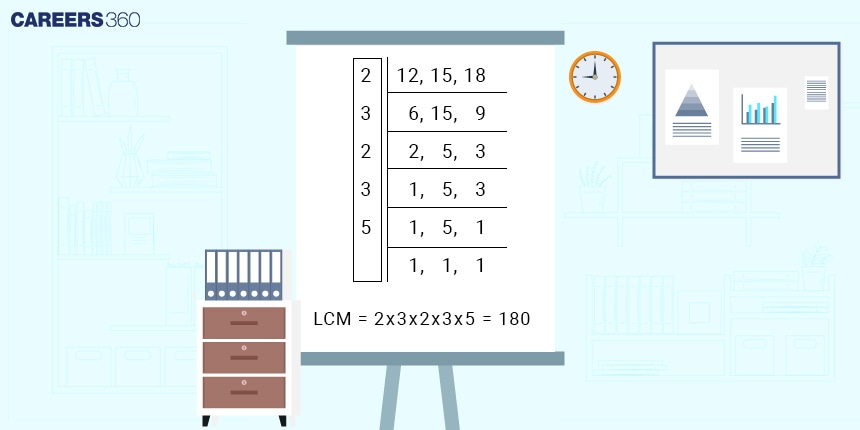
Therefore, the LCM of 12, 15, and 18 is 180.

Types of LCM Problems:

Problems of LCM can be divided into different categories as listed below:

1. LCM of two or more numbers if there is no remainder in each case:

If there is no remainder in each case then we can easily find the LCM of two more numbers using various methods such as prime factorisation, division method, listing method etc.

For example, find the least number which when divided by 12, 15, and 18 leaves no remainder in each case.

Sol: We need to find the LCM of 12, 15, and 18 to get the required number.

12 = 2 × 2 × 3

15 = 3 × 5

18 = 2 × 3 × 3

So, the LCM of 12, 15 and 18 is 2 × 2 × 3 × 3 × 5 = 180.

Therefore, the least number which when divided by 12, 15, and 18 leaves no remainder in each case is 180.

2. LCM of two or more numbers if there is an equal remainder in each case (Remainder is known):

In the case of LCM, if a single equal remainder is given, then firstly the LCM is calculated and then that single reminder is added to the LCM to get the required solution.

Example: Find the least number which when divided by 8, 12, 18, and 20 leaves the remainder of 3 in each case.

Here 8 = 2 × 2 × 2

12 = 2 × 2 × 3

18 = 2 × 3 × 3

20 = 2 × 2 × 5

So, the LCM of 8, 12, 18 and 20 is 2 × 2 × 2 × 3 × 3 × 5 = 360. In order to get the remainder of 3 in each case, we will add 3 to the LCM. So, the number is 360 + 3 = 363.

LCM of two or more numbers if there is equal remainder in each case (Remainder is known) but divisible by a given number:

We need to find the LCM of two or more numbers if there is equal remainder in each case (Remainder is known) but divisible by a given number.

Let’s understand it with the help of an example:

Find the least number which when divided by 2, 3, and 4 leaves a remainder of 1 in each case but is divisible by 5.

Sol: First of all find the LCM of 2, 3, and 4 which is 2 × 3 × 2 = 12.

Since the number when divided by 2, 3, and 4 leaves a remainder of 1 in each case,

So it is of the form 12k + 1, where k is any non-zero integer.

Let’s check if it is divisible by 5 by putting the value of k as 1, 2, 3, ….

For k = 1, 12k + 1 = 13, which is not divisible by 5.

For k = 2, 12k + 1 = 25, which is divisible by 5.

So, the least number which when divided by 2, 3, and 4 leaves a remainder of 1 in each case but is divisible by 5 is 25.

3. LCM of two or more numbers if the difference between divisor and remainder is the same in each case:

In the case of the difference between divisor and remainder is the same in each case. Then, firstly the LCM is calculated, and after that common difference between the number and its respective remainder is subtracted from that.

Example: Find the least number which when divided by 6, 10, 20, and 36 leaves remainders 4, 8, 18, and 34 respectively.

Sol: Here, the numbers are 6, 10, 20, and 36 and the respective remainders are 4, 8, 18, and 34 respectively. The difference between numbers and the respective remainders is equal to 2. So, first of all, find the LCM of 6, 10, 20, and 36.

Now, 6 = 2 × 3

10 = 2 × 5

20 = 2 × 2 × 5

36 = 2 × 2 × 3 × 3

So, the LCM of 6, 10, 20, and 36 is 2 × 2 × 3 × 3 × 5 = 180

Therefore, the required number is 180 – 2 = 178.

LCM of two or more numbers if the difference between divisor and remainder is the same in each case but divisible by a given number:

We need to find the LCM of two or more numbers if the difference between divisor and remainder is the same in each case but divisible by a given number.

Let’s understand it with the help of an example:

Find the least multiple of 13, which when divided by 6, 8, 10, and 12 leaves a remainder of 1, 3, 5, and 7 respectively.

Sol: Here in each case, the difference between the divisors and the remainder is the same, which is 6 - 1 = 8 - 3 = 10 - 5 = 12 - 7 = 5.

Now, the LCM of 6, 8, 10, and 12 is 2 × 2 × 2 × 3 × 5 = 120

So, the required number will be of the form 120k - 5, where k is any non-zero integer.

Now, we will check for divisibility by 13.

For k = 1, 120k - 5 = 115, which is not divisible by 13.

For k = 2, 120k - 5 = 235, which is not divisible by 13.

For k = 3, 120k - 5 = 355, which is not divisible by 13.

For k = 4, 120k - 5 = 475, which is not divisible by 13.

For k = 5, 120k - 5 = 595, which is not divisible by 13.

For k = 6, 120k - 5 = 715, which is divisible by 13.

Therefore, the required number is 715.

4. LCM of two or more numbers if the difference between divisor and remainder is not the same in each case:

5. LCM of two or more fractions:

To find the LCM of two or more fractions we use the formula below:

LCM of fraction = $\frac{\text{LCM of numerators}}{\text{HCF of denominators}}$

Example: Find the LCM of $\frac{2}{3}$ and $\frac{5}{12}$.

LCM of $\frac{2}{3}$ and $\frac{5}{12}$ = $\frac{\text{LCM of 2 and 5}}{\text{HCF of 3 and 12}}$

So, the required HCF of $\frac{2}{3}$ and $\frac{5}{12}$ is $\frac{10}{3}$.

Important properties of LCM:

• Property 1: The LCM of any two or more numbers is never less than any of the given numbers. For example, the LCM of 4 and 6 is 12, which is not less than 4 or 6.

• Property 2: The LCM of co-prime numbers is equal to the product between them. For example, the LCM of 20 and 21 is 20 × 21 = 420.

• Property 3: The order of the numbers does not affect the LCM. This means the LCM of a and b is the same as the LCM of b and a.

Relation between HCF and LCM and the two numbers:

The product of LCM and HCF of any two given natural numbers is equivalent to the product of the given numbers.

So, HCF of two numbers × LCM of two numbers = Product of two numbers

Also, HCF of two numbers = $\frac{\text{Product of two numbers}}{\text{LCM of two numbers}}$

Again, LCM of two numbers = $\frac{\text{Product of two numbers}}{\text{HCF of two numbers}}$

Tips and Tricks to solve the questions of HCF and LCM:

• The HCF of two or more numbers is smaller than or equal to the smallest number of given numbers.

• The largest or biggest number that exactly divides two numbers is the HCF of those numbers.

• The LCM of two or more numbers is greater than or equal to the greatest number of given numbers.

• The smallest or the least number which is divided by two or more numbers is the LCM of those numbers.

• If the ratio of two numbers is given as $a : b$ (where a and b are co-prime to each other) and the HCF of the two numbers is given as k, then we can easily find the two numbers as $ak$ and $bk$.

• Find HCF of 12 and 16.

Sol: Find the difference between 12 and 15. The difference is 3. Now, check whether the numbers are divisible by the difference. 12 is divisible by 3 and 15 is divisible by 3. So, the HCF is 4.

• Find LCM of 12, 24, and 36.

Sol: Choose the largest number. In this example, the largest number is 36. Check whether 36 is divisible by all other remaining numbers. 36 is divisible by both 12 and 24. So, the LCM is 36.

Practice questions:

Q.1. Find the least number divisible by 2, 3, 5, 6, 9, and 18 which is a perfect square.

1. 900

2. 400

3. 144

4. 3600

Hint: Find the LCM of 2, 3, 5, 6, 9, and 18.

Solution:

LCM of 2, 3, 5, 6, 9, and 18 = 90

$90 = 2 \times 3 \times 3 \times 5$

As 2 and 5 are not in pairs, we need to multiply 90 by 2 × 5 to make it a perfect square.

$\therefore 90 \times 2 \times 5 = 900$

Hence, the correct answer is option (1).

Q.2. The LCM of $(x^2 − 8x + 15)$ and $(x^2 − 5x + 6)$ is:

1. $(x − 2) (x − 3) (x − 5)$

2. $(x − 6)^2 (x + 1) (x − 3)$

3. $(x − 6) (x + 1) (x − 3)$

4. $(x + 6) (x + 1) (x − 3)$

Hint: The Least common multiple of two or more algebraic expressions is the expression of the lowest degree (or power) such that the expressions exactly divide it.

x2 − 8x + 15 = (x – 3) (x – 5)

x2 − 5x + 6 = (x – 2) (x – 3)

So, LCM (x2 − 8x + 15, x2 − 5x + 6)

= LCM {(x – 3), (x – 5), (x – 2) and (x – 3)}

= (x – 2) (x – 3) (x − 5)

Hence, the correct answer is option (1).

Q.3.The product of the two numbers is 1500 and their HCF is 10. The number of such possible pairs is/are:

1. 1

2. 3

3. 4

4. 2

Hint: Let the two numbers be $10x$ and $10y$, then find the value of $xy$ and find the possible number of pairs that are co-prime to each other.

Solution:

Given: The product of the two numbers is 1500 and their HCF is 10.

Let the two numbers be $10x$ and $10y$

So, $10x×10y=1500$

⇒ $100xy=1500$

⇒ $xy=15$

Now, 15 = 15 × 1 and 15 = 3 × 5

Therefore, the possible number of pairs that are co-prime to each other is 2.

Hence, the correct answer is option (4).

Q.4. The least common multiple of a and b is 42. The LCM of 5a and 11b is:

1. 2310

2. 4620

3. 210

4. 462

Hint: Multiply the LCM of (a, b) and the LCM of (5, 11) as 5 and 11 are co-prime numbers.

Solution:

The least common multiple of a and b is 42

According to the question,

LCM(a, b) = 42

LCM(5a, 11b) = LCM of (5, 11) $\times$ LCM of (a,b)

LCM(5a, 11b) = 55 $\times$ 42 = 2310

Hence, the correct answer is option (1).

Q.5. A number, when divided by 15 and 18 every time, leaves 3 as a remainder, the least possible number is:

1. 83

2. 103

3. 39

4. 93

Hint: Find the LCM of 15 and 18.

Solution:

Given,

A number, when divided by 15 and 18 every time, leaves 3 as a remainder.

LCM of 15 and 18 = 2 × 3 × 3 × 5 = 90

It leaves 3 as a remainder in each case

So, the required least number = 90 + 3 = 93

Hence, the correct answer is option (4).

Q.6. The ratio of the two numbers is 4 : 5, and their HCF is 3. What is their LCM?

1. 48

2. 80

3. 60

4. 36

Hint: Product of two numbers = LCM × HCF

Solution:

The ratio of the two numbers is 4 : 5.

Let the numbers be 4$x$, 5$x$.

Their HCF = $x$ as 4, 5 are coprime.

So, $x$ = 3

Numbers are 4 × 3 = 12, 5 × 3 = 15

We know the product of two numbers = LCM × HCF

⇒ 12 × 15 = LCM × 3

$\therefore$ LCM = 60

Hence, the correct answer is option (3).

Q.7. If three numbers are in the ratio of 1 : 3 : 7, and their LCM is 336, then their HCF is:

1. 16

2. 18

3. 10

4. 12

Hint: Assume the numbers are $x, 3x, 7x$ and their LCM = $21x$, which is equal to $336$.

Solution:

Three numbers are in the ratio of $1 : 3 : 7$.

Let the numbers be $x, 3x, 7x$.

Their LCM = $21x$

According to the question,

$21x = 336$

$\therefore x = 16$

So, the numbers are 16, 16 × 3 = 48, 16 × 7 = 112

$\therefore$ HCF of 16, 48, and 112 is 16.

Hence, the correct answer is option (1).

Q.8. The HCF of two numbers 960 and 1020 is:

1. 40

2. 120

3. 60

4. 80

Hint: HCF is the highest common factor. Find common factors between 960 and 1020.

Solution:

Factors of 960 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 5

Factors of 1020 = 2 × 2 × 3 × 5 × 17

Therefore, the HCF of 960 and 1020 = 2 × 2 × 3 × 5 = 60

Hence, the correct answer is option (3).

Q.9. Find the sum of the numbers between 550 and 700 such that when they are divided by 12, 16, and 24, leave the remainder of 5 in each case.

1. 1980

2. 1887

3. 1860

4. 1867

Hint: Find the LCM of 12, 16, and 24.

Solution:

LCM of 12, 16, and 24 = 48

Multiples of 48 which are between 550 and 700 such that they leave a remainder of 5 are:

48 × 12 + 5 = 581

48 × 13 + 5 = 629

48 × 14 + 5 = 677

Therefore, the sum of these numbers = 581 + 629 + 677 = 1887

Hence, the correct answer is option (2).

Q.10. The greatest four-digit number which is exactly divisible by 15, 24, and 40 is:

1. 9960

2. 9940

3. 9950

4. 9920

Hint: First, find the LCM of the given numbers. Then, find the remainder when the highest 4-digit number is divided by LCM.

Solution:

LCM of 15, 24, and 40 = 120

Greatest four-digit number = 9999

On dividing 9999 by 120,

9999 = 120 × 83 + 39

Remainder = 39

Therefore, the greatest number divisible by 15, 24, and 40 = 9999 – 39 = 9960

Hence, the correct answer is option (1).

Q.11. The LCM of $x$ and $y$ is 441 and their HCF is 7. If $x$ = 49 then find $y$.

1. 56

2. 36

3. 65

4. 63

Hint: Use the formula, LCM × HCF = $x$ × $y$

Solution:

Given:

LCM of $x$ and $y$ = 441, HCF = 7 and $x$ = 49

Now, LCM × HCF = $x$ × $y$

⇒ 441 × 7 = 49 × $y$

$\therefore y$ = $\frac{441}{7}$ = 63

Hence, the correct answer is option (4).

Q.12. Find the largest number which completely divides 24, 56, and 96.

1. 4

2. 1

3. 8

4. 2

Hint: First, factorise the given numbers. Then, find their HCF.

Solution:

24 = 2 × 2 × 2 × 3

56 = 2 × 2 × 2 × 7

96 = 2 × 2 × 2 × 2 × 2 × 3

The largest number which completely divides 24, 56, and 96

= HCF of 24, 56, and 96

= 2 × 2 × 2

= 8

Hence, the correct answer is option (3).

Q.13. The HCF and LCM of the two numbers are 126 and 9 respectively. If one of the numbers is 18, then what is the other number?

1. 63

2. 36

3. 84

4. 24

Hint: Let the two numbers be a and b. Then, a × b = HCF × LCM

Solution:

The product of two numbers is equal to the product of their HCF (Highest Common Factor) and LCM (Least Common Multiple).

Let the two numbers as a and b, with a = 18 (given). The HCF is 126 and the LCM is 9.

⇒ a × b = HCF × LCM

⇒ 18 × b = 126 × 9

⇒ b = 63

Hence, the correct answer is option (1).

Q.14. The sides of a triangular field are 62 m, 186 m, and 279 m. Find the greatest length of tape that would be able to measure each of them exactly without any fractions.

1. 62 m

2. 93 m

3. 31 m

4. 30 m

Hint: Calculate the highest common factor (HCF) of the sides of the triangular field i.e. 62 m, 186 m, and 279 m.

Solution:

The greatest length of tape that would be able to measure each side of the triangular field exactly without any fractions is the highest common factor (HCF) of the lengths of the sides.

Now, 62 = 31 × 2, 186 = 31 × 2 × 3 and 279 = 31 × 3 × 3

So, the HCF of 62, 186, and 279 is 31.

Hence, the correct answer is option (3).

Q.15. What is the greatest positive integer that divides 554, 714, and 213 leaving the remainder 43, 57, and 67 respectively?

1. 95

2. 71

3. 83

4. 73

Hint: By subtracting the remainder from the given numbers and taking HCF to get the answer.

Solution:

Deducting the remainder:

554 – 43 = 511

714 – 57 = 657

213 – 67 = 146

Now, Factors of 511 = 73 × 7

Factors of 657 = 73 × 3 × 3

Factors of 146 = 73 × 2

HCF of 551, 657, and 146 = 73

Hence, the correct answer is option (4).

Q.16. Find the LCM of 25, 30, 50, and 75.

1. 15

2. 150

3. 18

4. 75

Hint: The least common multiple (LCM) of two or more numbers is the lowest possible number that can be divisible by all the numbers.

Solution:

Factors of 25 = 5 × 5

Factors of 30 = 5 × 3 × 2

Factors of 50 = 5 × 5 × 2

Factors of 75 = 5 × 5 × 3

LCM of 25, 30, 50, and 75 = 5 × 5 × 3 × 2 = 150

Hence, the correct answer is option (2).

Q.17. The HCF of $\frac{3}{4}, \frac{7}{8}$, and $\frac{13}{14}$ is:

1. $\frac{1}{36}$

2. $\frac{1}{56}$

3. $\frac{1}{70}$

4. $\frac{1}{50}$

Hint: The highest common factor (HCF) of fractions is calculated as the HCF of the numerators divided by the least common multiple (LCM) of the denominators.

Solution:

The highest common factor (HCF) of fractions is calculated as the HCF of the numerators divided by the least common multiple (LCM) of the denominators.

HCF of the numerators (3, 7, 13) is 1.

LCM of the denominators (4, 8, 14) is 56.

So, HCF of $\frac{3}{4}, \frac{7}{8}$, and $\frac{13}{14}$ = $\frac{1}{56}$

Hence, the correct answer is option (2).

Q.18. The greatest number of five digits which is divisible by 13, 15, 18, and 21 is:

1. 99120

2. 98280

3. 96840

4. 95830

Hint: Find the least common multiple (LCM) of 13, 15, 18, and 21.

Solution:

The least common multiple (LCM) of 13, 15, 18, and 21 is 8190.

The greatest number of five digits is 99999.

We need to find the largest multiple of 8190 that is less than or equal to 99999.

Dividing 99999 by 8190 gives a quotient of 12 and a remainder.

The largest number less than 99999 that is divisible by 13, 15, 18, and 21 is 12 × 8190 = 98280

Hence, the correct answer is option (2).

Q.19. The ratio of the two numbers is 5 : 7 and their HCF is 3. Their LCM is:

1. 75

2. 125

3. 105

4. 35

Hint: The least common multiple (LCM) of two numbers is given by the product of the two numbers divided by their HCF.

Solution:

The two numbers are in the ratio 5 : 7, and their highest common factor (HCF) is 3. Therefore, the numbers are 5 × 3 = 15 and 7 × 3 = 21.

The least common multiple (LCM) of two numbers is given by the product of the two numbers divided by their HCF. So, the LCM of 15 and 21 is:

LCM = $\frac{15 \times 21}{3}$ = 105

Hence, the correct answer is option (3).

Q.20. Find the HCF of $\frac{11}{25}, \frac{9}{20}, \frac{16}{15}$, and $\frac{10}{33}$.

1. $\frac{1}{3300}$

2. $\frac{1}{330}$

3. $\frac{1}{33}$

4. $\frac{1}{300}$

Hint: The highest common factor (HCF) of fractions is calculated as the HCF of the numerators divided by the least common multiple (LCM) of the denominators.

Solution:

The highest common factor (HCF) of fractions is calculated as the HCF of the numerators divided by the least common multiple (LCM) of the denominators.

The numerators of the given fractions are 11, 9, 16, and 10.

The HCF of these numbers is 1.

The denominators of the given fractions are 25, 20, 15, and 33.

The LCM of these numbers is 3300.

Therefore, the HCF of the given fractions is $\frac{1}{3300}$.

Hence, the correct answer is option (1).