Linear Equations in One Variables: Definition, Questions, Formula, Examples

A linear equation in one variable is a fundamental concept in algebra that involves equations of the first degree. It is characterized by having one unknown variable. Understanding linear equations in one variable, including how to solve linear equations in one variable and the linear equations in one variable formula, lays the groundwork for more advanced mathematical concepts and problem-solving techniques. By practising linear equations in one variable questions and tackling various questions on linear equations in one variable, we can strengthen our algebraic skills and enhance our problem-solving abilities.

Linear Equation in One Variable: Definition

A linear equation in one variable is an algebraic equation that can be expressed in the form $ax+b=0$, where $a, b$ are constants and $a \neq 0$. The variable $x$ represents the unknown, and the equation involves only the first power of $x$. The solution to this equation is the value of $x$ that makes the equation true.

Example: $2x+3=0$ is a linear equation in one variable where $2, 3$ are constants and $x$ is the variable with the highest power of 1.

The standard form of Linear Equation in one Variable

The standard form of a linear equation in one variable is:

$ax + b = 0$, where $a, b$ are constants and $a \neq 0$. The variable $x$ represents the unknown, and the equation involves only the first power of $x$.

Solution of Linear Equation in One Variable

Solving a linear equation in one variable involves finding the value of the unknown variable that satisfies the equation. This process can be approached using various methods, including algebraic and graphical techniques, each providing a systematic way to isolate and determine the value of the variable.

Methods of Solving Linear Equations in One Variable

There are several methods to solve linear equations in one variable, each offering a unique approach to isolating the variable. The most common methods include the algebraic method, which involves manipulation of the equation, and the graphical method, which visualises the solution on a coordinate plane.

Algebraic Method

The algebraic method for solving a linear equation in one variable involves a series of steps to isolate the variable and find its value. Here's how to do it:

• Step 1: Simplify both sides of the equation by combining like terms and removing parentheses.

• Step 2: Move variable terms to one side of the equation. Add or subtract terms to get all variable terms on one side and all constant terms on the other side.

• Step 3: Divide or multiply both sides of the equation by the coefficient of the variable to solve for the variable.

• Step 4: Substitute the solution back into the original equation to ensure it satisfies the equation.

Example: Solve the linear equation $3x + \frac{x}{2} - 24 = 46$

Here, $3x + \frac{x}{2} - 24 = 46$

⇒ $3x + \frac{x}{2} = 46 + 24$
⇒ $\frac{7x}{2} = 70$

⇒ $x = \frac{70×2}{7}$

⇒ $x = 20$

Graphical Method

To solve a linear equation graphically:

• Plot the equation on a graph.

• The point where the line intersects the x-axis is the solution.

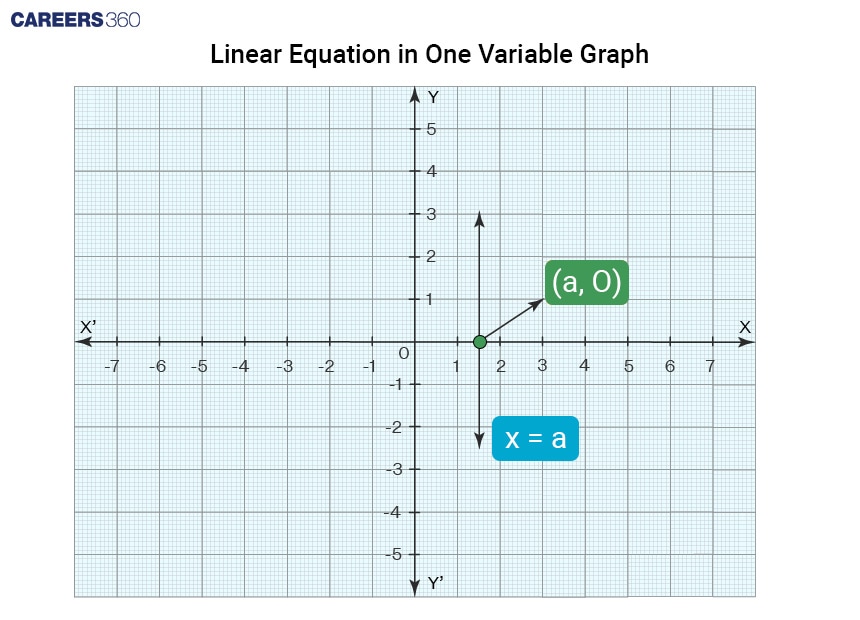
Given below is an example of the graphical method solution of the linear equation $x=a$, where the line $x=a$ intersects the x-axis at ($a$, 0).

Types of Solution

There can be only two types of solutions to a linear equation in one variable. These two solutions can either be a unique solution or an infinite many solutions.

Unique Solution

A linear equation in one variable typically has a unique solution. This means there is exactly one value of the variable that satisfies the equation.

Example: The solution of $2x-3=0$ is $x=\frac{3}{2}$, which is a unique solution of the equation.

Infinite Many Solutions

In certain cases, such as when the equation simplifies to a true statement (i.e. 0=0), there can be infinitely many solutions.

Example: The solutions of the equation $2x + 2 - 5 = 3x - x - 3$ are infinite as it is of the form $0=0$.

Examples of Word Problems on Linear Equations in One Variable

Example: There are three numbers where the first number is twice the second, and the second is thrice the third number. If the average of the three numbers is 20, what is the sum of the largest and smallest numbers?

Solution:

Let the third number be $x$.

According to the question,

The second number $= 3x$ and the first number $= 6x$.

So, $6x + 3x + x = 3 × 20$ (Sum of all three numbers)

⇒ $10x = 60$

⇒ $x = 6$

Therefore, the required sum $= 6x + x= 7x= 7 × 6 = 42$

Hence, the correct answer is 42.

Differentiate Linear Equation and Non-Linear Equation in one Variable

Differentiate Linear Equation in One Variable And Linear Equation in Two or More Variables

Tips and Tricks

• Always simplify the equation first.

• Check your solution by substituting it back into the original equation.

• Practice different types of linear equations to improve problem-solving skills.

Practice Questions/Solved Examples

Q.1.

If $\frac{5}{2}-\left (\frac{6}{5}\right )\left (x-\frac{15}{2} \right)=\frac{-x}{5}$, then what is the value of $x$?

1. $-\frac{23}{2}$

2. $\frac{13}{2}$

3. $-\frac{13}{2}$

4. $\frac{23}{2}$

Hint: Solve the equation to get the value of $x$.

Solution:

Given equation:

$\frac{5}{2}-\left (\frac{6}{5} \right )\left (x-\frac{15}{2}\right) =\frac{-x}{5}$

⇒ $\frac{5}{2}-\frac{6x}{5}+9=\frac{-x}{5}$

⇒ $\frac{5}{2} + 9=\frac{-x}{5} +\frac{6x}{5}$

⇒ $\frac{23}{2}=\frac{5x}{5}$

⇒ $x = \frac{23}{2}$

Hence, the correct answer is option (4).

Q.2.

If $\frac{10x}{3}+\frac{5}{2}(2-\frac{x}{3})=\frac{7}{2}$, then the value of $x$ is:

1. $\frac{3}{5}$

2. $-\frac{5}{3}$

3. $\frac{5}{3}$

4. $-\frac{3}{5}$

Hint: Use algebraic simplification to solve the equation.

Solution:

Given: $\frac{10x}{3}+\frac{5}{2}(2-\frac{x}{3})=\frac{7}{2}$

⇒ $\frac{10x}{3}+(5-\frac{5x}{6})=\frac{7}{2}$

⇒ $\frac{10x}{3}-\frac{5x}{6}=\frac{7}{2}-5$

⇒ $\frac{20x-5x}{6}=\frac{7-10}{2}$

⇒ $\frac{15x}{6}=-\frac{3}{2}$

⇒ $x=-\frac{3}{5}$

Hence, the correct answer is option (4).

Q.3.

If $\frac{x}{a+b}+1=\frac{x}{a-b}+\frac{a-b}{a+b}$, then $x$ is equal to:

1. $2a-b$

2. $a+b$

3. $a-b$

4. $2a+b$

Hint: Bring all the $x$ related terms to the left-hand side, then solve.

Solution:

Given:

$\frac{x}{a+b}+1=\frac{x}{a-b}+\frac{a-b}{a+b}$

⇒ $\frac{x}{a+b}-\frac{x}{a-b}=\frac{a-b}{a+b}-1$

⇒ $x(\frac{1}{a+b}-\frac{1}{a-b})=\frac{-2b}{a+b}$

⇒ $x(\frac{-2b}{(a+b)(a-b)})=\frac{-2b}{a+b}$

⇒ $x=(a-b)$

Hence, the correct answer is option (3).

Q.4.

If $\frac{1}{6}$ of $x$ – $\frac{7}{2}$ of $\frac{3}{7}$ equals to $(-\frac{7}{4})$, then the value of $x$ is:

1. – 1.5

2. – 3

3. – 2.5

4. – 6

Hint: Use the BODMAS rule.

Solution:

Given: $\frac{1}{6}$ of $x$ – $\frac{7}{2}$ of $\frac{3}{7}$ equals to $(-\frac{7}{4})$.

⇒ $\frac{1}{6} × x-\frac{7}{2} ×\frac{3}{7}= -\frac{7}{4}$

⇒ $\frac{x}{6} -\frac{3}{2}= -\frac{7}{4}$

⇒ $\frac{x}{6} =-\frac{7}{4}+\frac{3}{2}$

⇒ $\frac{x}{6} =-\frac{1}{4}$

⇒ $x =-\frac{3}{2}$

⇒ $x=-1.5$

Hence, the correct answer is option (1).

Q.5.

If $(-\frac{1}{2}) \times (x-5) + 3 = -\frac{5}{2}$, then what is the value of $x$?

1. 16

2. 4

3. – 6

4. – 4

Hint: Use the concept of BODMAS to solve.

Solution:

Given:

$(-\frac{1}{2}) \times (x-5) + 3 = -\frac{5}{2}$

⇒ $-\frac{1}{2}x + \frac{5}{2} + 3 = -\frac{5}{2}$

⇒ $-\frac{1}{2}x + \frac{11}{2} = -\frac{5}{2}$

⇒ $-\frac{1}{2}x = -\frac{16}{2}$

⇒ $x = 16$

Hence, the correct answer is option (1).

Q.6.

A man hired a domestic helper under the agreement to pay him Rs. 90 and provide a turban after one year of service. However, the domestic helper worked only for nine months and received Rs. 65 along with the turban. Determine the price of the turban.

1. Rs. 25

2. Rs. 18.75

3. Rs. 10

4. Rs. 2.50

Hint: Let the price of the turban be Rs. $x$, then create a linear equation and solve it.

Solution:

Let the price of the turban be Rs. $x$.

Condition:

12 month payment $= 90 + x$

1 month payment $= \frac{90+x}{12}$

9 month payment = $\frac{90+x}{12}×9$

He worked for 9 months and got Rs. 65 and a turban.

$\frac{90+x}{12} × 9 = 65 + x$

⇒ $\frac{90+x}{4} × 3 = 65 + x$

⇒ $270 + 3x = 260 + 4x$

$\therefore x = 10$

Hence, the correct answer is option (3).

Q.7.

If $5x-40=3x$, then the numerical value of $(2x-11)$ is:

1. 29

2. 39

3. 19

4. 9

Hint: Find the value of $x$ from $5x-40=3x$

Solution:

Given:

$5x-40=3x$

$⇒5x-3x=40$

$⇒2x=40$

$\therefore x=20$

Substituting the value of $x$ in $(2x-11)$, we get,

$(2x-11)=2(20)-11=29$

Hence, the correct answer is option (1).

Q.8.

What is the value of $x$ for which the expressions $8x+12$ and $14x-6$ become equal?

1. 1

2. 3

3. 6

4. 9

Hint: Find the value of the unknown by solving and simplifying the expression given.

Solution:

Given: The equations are $8x+12$ and $14x-6$.

According to the question,

$8x+12 = 14x-6$

$⇒12+6 = 14x-8x$

$⇒6x = 18$

$\therefore x = 3$

Hence, the correct answer is option (2).

Q.9.

If $(6x-5)=(4x+7)$, then the numerical value of $(x+1)^3$ is:

1. 216

2. 125

3. 64

4. 343

Hint: Find the value of the unknown by solving and simplifying the given expression.

Solution:

Given: $(6x-5) = (4x+7)$

$⇒6x-4x = 7+5$

$⇒2x = 12$

$\therefore x = 6$

Now, $(x+1)^{3}$ is given as,

$(6+1)^{3} = 343$

Hence, the correct answer is option (4).

Q.10.

If $(9-3x)-(17x-10)=1$, then the value of $x$ is:

1. $1$

2. $-1$

3. $\frac{9}{10}$

4. $–\frac{9}{10}$

Hint: Find the value of the unknown by solving and simplifying the expression given.

Solution:

Given: $(9-3x)-(17x-10) = 1$

$⇒9-3x-17x+10 = 1$

$⇒-20x+19 = 1$

$\therefore x = \frac{18}{20} = \frac{9}{10}$

Hence, the correct answer is option (3).