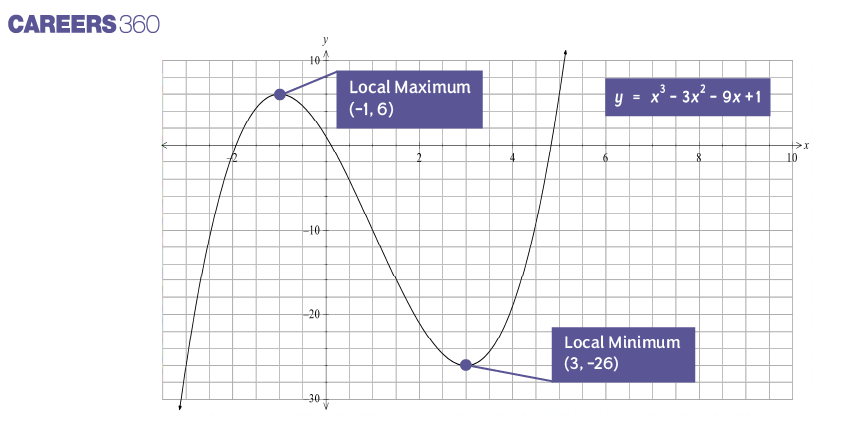
Maxima and Minima in polynomials: Definition, Questions, Calculator

The Maxima and Minima of a polynomial is a very important chapter of mathematics. In a polynomial function, the maxima is the highest point and the minima is the lowest point and the graph looks like a parabola. To find the maxima and minima of polynomials, we need to find the maximum and minimum values of the polynomial. Because the shape of the graph depends on these values. The graph of maximum and minimum values of a quadratic polynomial, ax2 + bc +c opens upwards if have a minimum value and opens downwards if have a maximum value. We will discuss these topics in detail in this article.

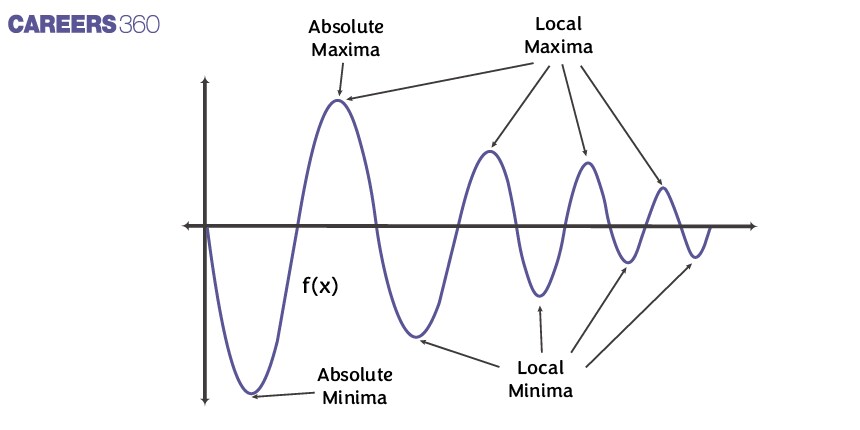
What are Absolute maxima and Absolute Minima?

The highest value of a given polynomial f(x) in the interval [a, b] is called the Absolute maxima.

Suppose f(c) is the maximum value such that f(c) $\geq$ f(x) for all values of x in the interval [a, b].

The lowest value of a given polynomial f(x) in the interval [a, b] is called the Absolute minima.

Suppose f(d) is the minimum value such that f(d) $\leq$ f(x) for all values of x in the interval [a, b].

Find the absolute maxima and minima of polynomial f(x) = x2 – 4x + 3 in the interval [0, 3]

f(0) = 0 - 0 + 3 = 3

f(1) = 1 - 4 + 3 = 0

f(2) = 4 - 8 + 3 = -1

f(3) = 9 - 12 + 3 = 0

The highest value of f(x) in the interval [0, 3] is 3.

The lowest value of f(x) in the interval [0, 3] is -1.

So, absolute maxima when x = 0 and absolute minima when x = 2

How to find the minimum and maximum value of a polynomial?

There are two main methods to find a polynomial's maximum and minimum values.

• Graphical method

• Algebraic method

We have discussed both methods below.

Graphical Method

In the graphical method, we have to plot the polynomial function on a coordinate plane and visually identify the highest and lowest points on the graph.

Steps are:

Step 1: First plot the graph of the polynomial function say f(x) by hand or in any graphical area.

Step 2: Find the maximum and minimum points of the graph. These points are often located where the slope of the curve changes, which corresponds to the critical points of the polynomial.

Step 3: Then check using other methods whether those points are right or not.

Critical points occur where the derivative of the polynomial is zero or undefined.

Algebraic Method

In the algebraic method, we use calculus to find the critical points and then determine whether these points are maxima, minima, or neither.

It also involves a few steps.

Those steps are:

Step 1: Calculate the first derivative of the polynomial f(x), say f’(x).

Step 2: Equate the first derivative to 0 to get the critical point or points. i.e., f’(x) = 0

Step 3: Then find the 2nd derivative say f’’(x) to check the nature of the critical points.

If f’’(x) > 0, then it is a local minimum, and if f’’(x) < 0, then it is a local maximum.

Step 4: If the polynomial is defined on a closed interval, then evaluate the functions at the endpoints of the interval.

Step 5: Compare the values to determine the absolute maximum and minimum.

Example:

Maxima and Minima for a Quadratic Polynomial

A quadratic polynomial will be in the form ax2 + bx + c = 0 and a graphical form of a quadratic polynomial in a parabola shape that can either open upwards or downwards. The vertex of the parabola represents the maximum or minimum value of the quadratic polynomial depending on which direction the parabola opens.

Let $f(x)=a x^2+b x+c$ be a quadratic function given by the points $(h, k)$,,

Then

h = $-\frac{b}{2a}$

k = f(h) = $a(-\frac{b}{2a})^2 + b (-\frac{b}{2a}) + c$ = $-\frac{b^2}{4a} + c$

So, vertex point = (h, k) = $(-\frac{b}{2a}, -\frac{b^2}{4a} + c)$

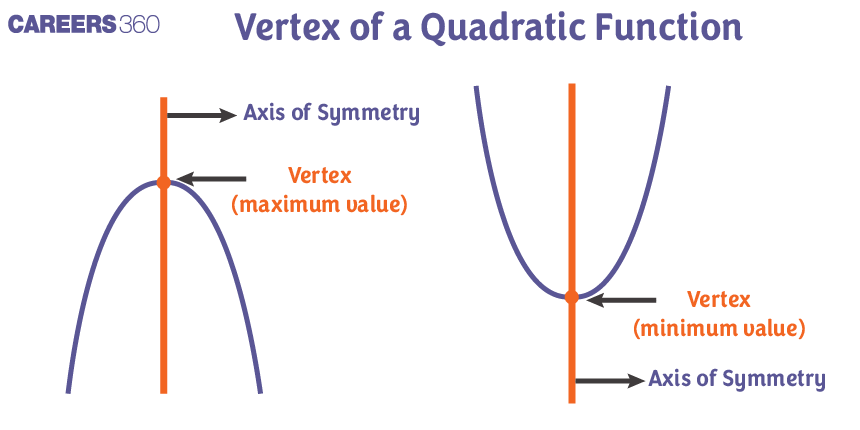
If the value of a > 0, the parabola opens upwards and the minimum value of the quadratic polynomial is obtained at the vertex point.

If the value of a < 0, the parabola opens downwards and the maximum value of the quadratic polynomial is obtained at the vertex point.

Questions based on the Power increase/decrease

When we multiply two polynomials, the powers of the variables in each term are added together.

Example: a3 × a5 = a3 + 5 = a8

When we divide one polynomial by another, the powers of the variables in the terms are subtracted.

Example: a5 ÷ a3 (dividing a5 by a3 ) = a5 – 3 = a2

If we raise a polynomial to a power, we have to multiply the powers of the variable.

Example: Raising a5 to the 2nd power, (a5)2 = a5 × 2 = a10

When we take the square root of a polynomial, the powers of the variables are divided by 2.

Example: Square root of a10 = a10 ÷ 2 = a5

If we subtract or eliminate the highest power of a polynomial, then the degree of that polynomial decreases to the next highest power present in the remaining terms.

Example:

2x4 + 3x2 – x + 2 is a polynomial of degree 4.

If we subtract 2x4 from the polynomial then the polynomial becomes 3x2 – x + 2 and the degree of the polynomial becomes 2 which is the next highest power present in the remaining terms.

Example:

If $x=-1$, then the value of $\frac{1}{x^{99}}+\frac{1}{x^{98}}+\frac{1}{x^{97}}+\frac{1}{x^{96}}+\frac{1}{x^{95}}+\frac{1}{x^{94}}+\frac{1}{x}-1$ is:

We have,

$\frac{1}{x^{99}}+\frac{1}{x^{98}}+\frac{1}{x^{97}}+\frac{1}{x^{96}}+\frac{1}{x^{95}}+\frac{1}{x^{94}}+\frac{1}{x}-1$

Substituting value of $x=–1$ in the given expression,

$=\frac{1}{(–1)^{99}}+\frac{1}{(–1)^{98}}+\frac{1}{(–1)^{97}}+\frac{1}{(–1)^{96}}+\frac{1}{(–1)^{95}}+\frac{1}{(–1)^{94}}+\frac{1}{(–1)}-1$

$=-1+1-1+1-1+1-1-1$

$=–2$

Hence, the correct answer is –2.

Fractional Algebra

Fractional algebra is a very important part of Mathematics. It involves fractions to do operations. Fractions mean expressions in the form $\frac{a}{b}$, where a and b are integers, b $\neq$ 0

In the context of algebra, fractions can include variables and polynomials as well.

Some of the operations on fractions in algebra are discussed below.

Simplifying Fractions:

We have to divide the numerator and denominator by their Greatest Common Divisor(GCD).

$\frac{6}{9}$

Here GCD of 6 and 9 is 3.

Now we have to divide the numerator and denominator by 3.

So, simplified version of above fraction is $\frac{2}{3}$

Addition of Fractions in Algebra

To add two fractions they must have the same denominator.

So, we have to find the least common denominator and rewrite each fraction with this denominator.

$\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}$

Subtraction of Fractions in Algebra

Subtraction process of fractions in algebra is the same as Addition.

To subtraction two fractions they must have the same denominator.

So, we have to find the least common denominator and rewrite each fraction with this denominator.

$\frac{a}{b}-\frac{c}{d}=\frac{ad-bc}{bd}$

Multiplication of Fractions in Algebra

To multiply two or more fractions, just multiply the numerators and denominators.

$\frac{a}{b} × \frac{c}{d} = \frac{ac}{bd}$

Division of Fractions in Algebra

To divide one fraction by another, we have to multiply the dividend fraction by the reciprocal of the divisor factor.

If we want to divide $\frac{a}{b}$ by $\frac{c}{d}$, then have to find the reciprocal of $\frac{c}{d}$, which is $\frac{d}{c}$

Now, multiply to get the result.

$\frac{a}{b} × \frac{d}{c} = \frac{ad}{bc}$

Rational expressions

A rational expression is a fraction where the numerator and/or the denominator are polynomials.

There are two processes to simplify these expressions.

Either Factorize them and eliminate the common factors.

Or,

To add or subtract find the least common denominator and combine.

To multiply or divide, simply multiply or divide the numerators and denominators as basic fractions.

Example:

If $\left (x+\frac{1}{x}\right )=5$, find the value of $\frac{6x}{x^{2}+x+1}$.

Given: $\left (x+\frac{1}{x} \right)=5$

⇒ $\frac{x^2+1}{x}=5$

⇒ $x^2+1=5x$

Adding $x$ on both sides,

⇒ $x^2+1+x=5x+x$

⇒ $x^2+x+1=6x$

Now, put the value of $x^2+x+1=6x$ in the expression $\frac{6x}{x^{2}+x+1}$

So, $\frac{6x}{x^{2}+x+1}=\frac{6x}{6x}=1$

Hence, the correct answer is 1.

Important Points

• The highest value of a given polynomial f(x) in the interval [a, b] is called the Absolute maxima.

• The lowest value of a given polynomial f(x) in the interval [a, b] is called the Absolute minima.

• To add or subtract two fractions, we have to find the least common denominator and rewrite each fraction with this denominator.

• To divide one fraction by another, we have to multiply the dividend fraction by the reciprocal of the divisor factor.

• To multiply two or more fractions, just multiply the numerators and denominators.

Tips and Tricks

• Critical points occur where the derivative of the polynomial is zero or undefined.

• To simplify fractions, divide the numerator and denominator by their Greatest Common Divisor(GCD).

• For polynomials of degree n, consider the leading term anxn to determine the end behaviour.

• Use the graphical method to visually identify the maxima and minima.

• If the problem involves a specific interval, evaluate the polynomial at the endpoints and compare it with critical points within the interval.

Practice Questions

Q1. The maximum value of $5+20x-4x^{2}$, when $x$ is a real number, is:

1. 1

2. 5

3. 25

4. 30

Hint: If an expression is in the form of $ax^{2}+bx+c$, then the maximum value is given by ($c-\frac{b^2}{4a}$).

Answer:

Given: $5+20x-4x^{2}$

If an expression is in the form of $ax^{2}+bx+c$, then the maximum value is given by ($c-\frac{b^2}{4a}$).

Here, $c = 5$, $b = 20$ and $a = -4$

$\therefore$ Maximum value = $5-\frac{20^2}{4×(–4)}$

= $5 - \frac{400}{–16}$

= $5-(-25)$

= $30$

Hence, the correct answer is 30.

Q2. If $2x+\frac{9}{x}=9$, what is the minimum value of $x^2+\frac{1}{x^2}$?

1. $\frac{95}{36}$

2. $\frac{97}{36}$

3. $\frac{86}{25}$

4. $\frac{623}{27}$

Hint: You have to multiply both sides of the first equation by $x$, then factorise to get the value of $x$ to solve it.

Answer:

Given:

$2x+\frac{9}{x}=9$

Multiplying both sides by $x$, we get,

$⇒2x^2-9x+9=0$

$⇒(2x-3)(x-3)=0$

So, $x= \frac{3}{2},3$

Putting the values of $x$ in the equation, we get

When $x=\frac{3}{2}$,

$x^2+\frac{1}{x^2}=(\frac{3}{2})^2+\frac{1}{(\frac{3}{2})^2}=\frac{97}{36}=2.69$

When $x=3$,

$x^2+\frac{1}{x^2}=3^2+\frac{1}{3^2}=\frac{82}{9}=9.11$

So, the minimum value is $\frac{97}{36}$.

Hence, the correct answer is $\frac{97}{36}$.

Q3. If $2x-6\leq x-3$ and $1+3x<4x+4$, then $x$ can take which of the following values?

1. 4

2. -4

3. -6

4. 2

Hint: Simplify the given expression and find the range of values of $x$.

Answer:

Given: $2x-6\leq x-3$ and $1+3x<4x+4$

⇒ $2x-x\leq 6-3$ and $-4+1<4x-3x$

⇒ $x\leq 3$ and $-3<x$

⇒ $-3<x\leq 3$

Amongst all the given values, 2 satisfies the above condition.

Hence, the correct answer is 2.

Q4. If $2x-4\leq \frac{2-x}{3}$ and $2(2x+5)>3x-5$, then $x$ can take which of the following values?

1. -14

2. 3

3. 4

4. 14

Hint: Simplify the given expression and find the range of values of $x$.

Answer:

Given: $2x-4\leq \frac{2–x}{3}$ and $2(2x+5)>3x-5$

⇒ $3×(2x-4)\leq 2-x$ and $(4x+10)>3x-5$

⇒ $(6x-12)\leq 2-x$ and $(4x-3x)>-5-10$

⇒ $(6x+x)\leq 2+12$ and $(4x-3x)>-15$

⇒ $7x\leq14$ and $x>-15$

⇒ $x\leq2$ and $x>-15$

⇒ $-15<x\leq2$

Amongst all the given values –14 satisfies the above condition.

Hence, the correct answer is –14.

Q5. The minimum value of $2\sin^{2}\theta+3\cos^{2}\theta$ is:

1. 0

2. 3

3. 2

4. 1

Hint: Use: $\cos^{2}\theta = 1-\sin^{2}\theta$ and also the maximum value of $\sin^{2}\theta$ = 1.

Answer:

Given: $2\sin^{2}\theta+3\cos^{2}\theta$

= $2\sin^{2}\theta+3(1-\sin^{2}\theta)$

= $2\sin^{2}\theta+3-3\sin^{2}\theta)$

= $3-\sin^{2}\theta$

For minimum value of $(3-\sin^{2}\theta)$ by putting $\sin^{2}\theta=1$

⇒ $3-1=2$

Hence, the correct answer is 2.

Q6. If $a^{2}=b+c,b^{2}=c+a,c^{2}=a+b$, the value of $3\left (\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}\right)$ is:

1. 1

2. $\frac{1}{3}$

3. 3

4. 4

Hint: Multiply the numerator and the denominator of each term of $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}$ by $a,b$, and $c$ respectively and put the given values of $a^2,b^2$, and $c^2$.

Answer:

Given: $a^{2}=b+c,b^{2}=c+a$, and $c^{2}=a+b$

Now, $\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}$

= $\frac{a}{a^2+a}+\frac{b}{b^2+b}+\frac{c}{c^2+c}$ (multiplying the numerator and the denominator of each term by $a,b$, and $c$ respectively)

= $\frac{a}{b+c+a}+\frac{b}{c+a+b}+\frac{c}{a+b+c}$ (putting the values of $a^2,b^2$ and $c^2$)

= $\frac{a+b+c}{a+b+c}$

= $1$

So, $3\left (\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}\right)=3×1=3$

Hence, the correct answer is $3$.

Q7. If $\left (a+\frac{1}{b} \right)=1$ and $\left (b+\frac{1}{c} \right)=1$, the value of $\left (c+\frac{1}{a} \right)$ is:

1. 0

2. 1

3. -1

4. 2

Hint: Find the values of $c$ and $a$ from the given equations and put them in the given expression.

Answer:

Given:

$a+\frac{1}{b}=1$ and $b+\frac{1}{c}=1$

⇒ $a =1-\frac{1}{b}=\frac{(b-1)}{b}$

⇒ $\frac{1}{a}=\frac{b}{(b-1)}=\frac{-b}{(1-b)}$

Also, $b+\frac{1}{c}=1$

⇒ $\frac{1}{c} =1-b$

⇒ $c = \frac{1}{(1-b)}$

Now, $c + \frac{1}{a}$

$=\frac{1}{(1-b)}-\frac{b}{(1-b)}$

$=\frac{(1-b)}{(1-b)}$

$= 1$

Hence, the correct answer is 1.

Q8. Find the value of $a$ in the following equation. (Given $a<10 $)

$\frac{(187 \div 17 \times a-3 \times 3)}{\left(8^2-9 \times 7+a^2\right)}=1$

1. 2

2. 1

3. 4

4. 3

Hint: Simplify the equation and find the value of $a$, where $a<10 $.

Answer:

$\frac{(187 \div 17 \times a-3 \times 3)}{\left(8^2-9 \times 7+a^2\right)}=1$

$⇒\frac{(11a-9)}{\left(a^2+1\right)}=1$

$⇒11a - 9 = a^2 + 1$

$⇒a^2 - 11a + 10 = 0$

$⇒(a - 10)(a - 1) = 0$

$⇒a = 10$ and $a = 1$

Since $a<10$

So, $a = 1$

Hence, the correct answer is 1.

Q9. If $x^2-3.2 x+1=0$ and $x>1$, the value of $x^2-\frac{1}{x^2}$ is:

1. $16.8 \sqrt{0.39}$

2. $12.8 \sqrt{0.39}$

3. $16.8 \sqrt{0.32}$

4. $12.8 \sqrt{0.32}$

Hint: Use the following identities.

$(x-y)^2=x^2-2xy+y^2$ and $(x+y)(x-y)=x^2-y^2$

Answer:

Given: $x^2-3.2 x+1=0$ and $x>1$

$x^2-3.2 x+1=0$

Dividing both sides by $x$, we get,

$⇒x-3.2 +\frac{1}{x}=0$

$⇒x+\frac{1}{x}=3.2 $---(1)

Squaring both sides, we get,

$⇒x^2+\frac{1}{x^2}+2=10.24 $

$⇒x^2+\frac{1}{x^2}-2=6.24 $

$⇒(x-\frac{1}{x})^2=6.24 $

$⇒(x-\frac{1}{x})=\sqrt{6.24}$---(2)

Multiplying 1 and 2,

$(x+\frac{1}{x})(x-\frac{1}{x})=3.2×\sqrt{6.24}=3.2×\sqrt{16×0.39}=12.8 \sqrt{0.39}$

Hence, the correct answer is $12.8 \sqrt{0.39}$.

Q10. If $x+\frac{1}{x}=2$, then the value of $x^{11}+\frac{1}{x^{20}}$ is:

1. 01

2. 1

3. 2

4. 7

Hint: Simplify the given equation and find the value of $x$.

Use $(a-b)^2=a^2+b^2-2ab$

Answer:

Given, $x+\frac{1}{x}=2$

⇒ $x^2+1=2x$

⇒ $x^2+1-2x=0$

⇒ $(x-1)^2=0$

⇒ $x-1=0$

$\therefore x=1$

Consider, $x^{11}+\frac{1}{x^{20}}$

= $1^{11}+\frac{1}{1^{20}}$

= $1+1$

= $2$

Hence, the correct answer is 2.

Q11. If $2+4x<5-\frac{x}{2}$ and $3x+3>-5-3x$, then $x$ can take which of the following values?

1. 1

2. 2

3. -2

4. -1

Hint: Simplify the given expression and find the range of values of $x$.

Answer:

Given: $2+4x<5-\frac{x}{2}$ and $3x+3>-5-3x$

⇒ $2+4x<\frac{10-x}{2}$ and $3x+3x>-5-3$

⇒ $2(2+4x)<10-x$ and $6x>-8$

⇒ $4+8x<10-x$ and $x>\frac{-8}{6}$

⇒ $x+8x<10-4$ and $x>\frac{-4}{3}$

⇒ $9x<6$ and $x>-1.33$

⇒ $x<\frac{6}{9}$ and $x>-1.33$

⇒ $x<0.67$ and $x>-1.33$

⇒ $-1.33<x<0.67$

Amongst all the given values –1 satisfies the above condition.

Hence, the correct answer is –1.