Mixture and Alligation: Questions, Formula, Examples, Mock Test

‘Mixture and Alligation’ is an important concept in mathematics, especially useful in solving problems related to the mixing of two or more components with different characteristics, such as cost, concentration, or quantity. This topic is widely applied in various fields, including chemistry, commerce, and everyday problem-solving. The mixture and alligation formula is crucial for solving these problems efficiently. Mixture and alligation questions for competitive exams, such as those for bank and SSC CGL, often test this concept. Practicing mixture and alligation questions with solutions can help prepare for these exams.

Concept of Mixture and Alligation

Mixture: When we combine two or more substances to form a single homogeneous entity, it is called a mixture.

Alligation: A rule that helps in finding the mean value of a mixture when the quantities and prices of the ingredients are known.

Mixture and Alligation involves combining two or more quantities with different prices, concentrations, or values to achieve a desired mixture. There are two main types of problems:

Types of Problems

1. Simple Mixture Problems: Involving the combination of two or more substances. For example, mixing two different types of tea to get the desired price per kilogram.

2. Replacement Problems: Involving the removal and addition of a substance from a mixture. For example, replacing a part of a salt solution with water to change its concentration.

Mixture and Alligation: Formula

There are various formulas used to solve problems related to mixture and alligation. Let us discuss them one by one with proper examples.

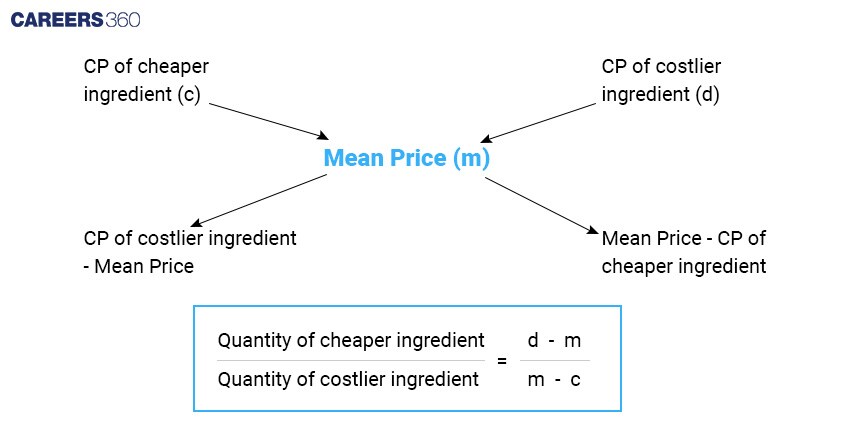
Rule of Alligation:

The rule of alligation is used to find the ratio in which two or more ingredients at different prices (or concentrations) must be mixed to produce a mixture at a given price (or concentration).

Formula: $\frac{Quantity \space of \space Cheaper}{Quantity \space of \space Dearer}$ = $\frac{\text{Dearer price - Mean price}}{\text{Mean price - Cheaper price}}$

Example: One litre of milk costs INR 40. Water is mixed with milk and the mixture cost becomes INR 30 per litre. Find the ratio of water and milk in the mixture.

Solution: Given: That one litre of milk costs INR 40.

Water is mixed with milk and the mixture cost becomes INR 30 per litre.

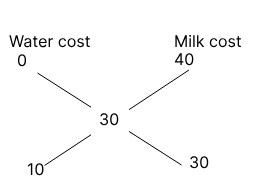
The ratio of water and milk in the mixture = $10:30$ = $1:3$

Hence, the correct answer is $1:3$.

Weighted Average to solve the problems of Mixture and Alligation:

The weighted average method helps in finding the average price (or concentration) of a mixture.

Formula: Weighted Average = $\frac{Q_1×P_1 + Q_2×P_2 + Q_3×P_3 + …….}{Q_1 + Q_2 + Q_3 + …….}$

Where $Q_1, Q_2, Q_3,....$ are quantities and $P_1, P_2, P_3,.....$ are its respective prices or concentration.

Example: The average height of 30 boys in a class is 160 cm. If the average height of the other 20 boys is 165 cm, the average height of the whole class (in cm) is:

Solution: Average height of 30 boys = 160 cm

The average height of the other 20 boys = 165 cm

We have to find out the average height of the whole class which is

= $\frac{30\times 160 + 20\times 165}{30 + 20}$

= $\frac{4800 + 3300}{50}$

= $\frac{8100}{50}$ = 162 cm.

Hence, the correct answer is 162 cm.

Rule of constant:

In this rule, we target the element in the mixture whose amount does not change but its percentage changes because of the change in the total amount of the mixture.

Example: How many litres of pure water should be added to 50 litres of 30% milk solution so that the resultant mixture is a 20% milk solution?

Solution: The quantity of milk in the solution is $50×\frac{30}{100}=15$ litres, and it will remain the same in the new solution as well.

So, 15 liters = 30% of the first solution =20% of the new solution

Therefore, the quantity of new solution = $15×\frac{100}{20}$ = 75 litres.

Now, the increase in the quantity of the new mixture is because of adding extra water.

Hence, the quantity of water added = 75 – 50 = 25 litres.

Mixture and Alligation: Concept of Replacement

Replacement problems involve removing a part of the mixture and replacing it with another substance, which often results in a change in the overall concentration.

The formula for replacement in the mixture

Final concentration = Initial concentration × $[1-\frac{\text{Quantity Replaced}}{\text{Total Quantity}}]^n$

where $n$ is the number of times the replacement occurs.

Example: From a cask of milk containing 64 litres, 8 litres are drawn out and the cask is filled up with water. If the same process is repeated a second, then a third time, what will be the proportion of milk to water in the resulting mixture?

Solution: The amount replaced by water each time is 8 litres.

The amount of milk = Initial amount$\times(1- \frac{\text{Amount replaced by water}}{\text{Total Amount}})^n$, where $n$ = No. times process repeated

So, the amount of milk

$= 64\times (1-\frac{8}{64})^3$

$= 64\times (1-\frac{1}{8})^3$

$= 64\times (\frac{7}{8})^3$

$= 64\times \frac{7\times 7\times7}{8\times 8\times 8}$

$= \frac{343}{8}$

Amount of water $= 64 - \frac{343}{8}= \frac{169}{8}$

So, the required ratio $=\frac{343}{8}:\frac{169}{8} =343:169$

Hence, the correct answer is $343:169$.

Tips and Tricks

• Always identify the different substances and their concentrations or prices accurately.

• Choose between the rule of alligation, weighted average, and rule of constant based on the problem type.

• Simplify the ratios in alligation problems to make calculations easier.

• Ensure all quantities are in the same units before applying formulas.

Practice Questions/Solved Examples

Q.1.

In what ratio should sugar at Rs. 30 per kg be mixed with sugar at Rs. 45 per kg so that, on selling the mixture at Rs. 42 per kg, there is a profit of 20%?

1. $2:1$

2. $2:3$

3. $5:2$

4. $3:5$

Hint: Use the concept of alligation:

Required ratio = (Higher value – Mean value) : (Mean value – Lower value)

Solution:

Let the cost price (CP) of sugar A be Rs. 30 and sugar B be Rs. 45.

Let the CP of the mixture be Rs. $x$.

Now, $\frac{120x}{100}$ = 42

$\therefore x$ = 35

Using the concept of alligation we have,

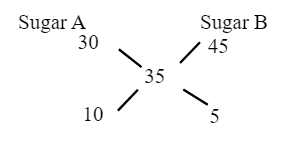
Required ratio = (Higher value – Mean value) : (Mean value – Lower value)

= $(45 - 35):(35 - 30)$ = $10:5 = 2:1$

Hence, the correct answer is option (1).

Q.2.

In what ratio should tea at Rs. 240 per kg be mixed with tea at Rs. 280 per kg so that, on selling the mixture at Rs. 324 per kg, there is a profit of 20%?

1. $1:1$

2. $1:2$

3. $1:3$

4. $1:4$

Hint: Required ratio = (Higher value – Mean value) : (Mean value – Lower value)

Solution:

Let the cost price (CP) of Tea A = Rs. 240 and CP of Tea B = Rs. 280

Let the CP of the mixture be Rs. $x$.

The mixture is sold at Rs. 324 with a gain of 20%.

So, $\frac{120x}{100}$ = 324

$\therefore x$ = 270

Thus, the CP of the mixture is Rs. 270.

Now, using the concept of alligation, we get,

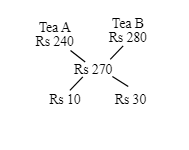
Required ratio

= (Higher value – Mean value) : (Mean value – Lower value)

= $(280 - 270):(270 - 240) = 10:30 = 1:3$

Hence, the correct answer is option (3).

Q.3.

A vessel contains 20 L of acid. 4 L of acid is taken out of the vessel and replaced by the same quantity of water. Next, 4 L of the mixture is withdrawn and again the vessel is filled with the same quantity of water. The ratio of the quantity of acid left in the vessel with the quantity of acid initially in the vessel is:

1. $4:5$

2. $4:25$

3. $16:25$

4. $1:5$

Hint: Use this formula =

Initial quantity ×$(1-\frac{\text{Quantity taken out}}{\text{Original quantity}})^{\text{number of times removed}}$

Solution:

Here,

Remaining acid = Initial quantity × $(1–\frac{\text{Quantity taken out}}{\text{Original quantity}})^{\text{number of times removed}}$

⇒ Remaining acid $=20×(1-\frac{4}{20})^2=20×\frac{4}{5}×\frac{4}{5}= 12.8$ L

So, the required ratio

= $(12.8):(20)$

= $128:200$

= $16:25$

Hence, the correct answer is option (3).

Q.4.

A drum contains 80 litres of ethanol. 20 litres of this liquid is removed and replaced with water. 20 litres of this mixture is again removed and replaced with water. How much water (in litres) is present in this drum now?

1. 45

2. 40

3. 35

4. 44

Hint: Use this formula:

Quantity of ethanol after replacement = ${\text{total mixture}×(\frac{(\text{total mixture – liquid removed}}{\text{total mixture}})^{\text{number of times liquid is replaced}}}$

Solution:

Total volume of mixture = 80 litres

Liquid replaced with water is 20 litres and this process is repeated two times.

Pure ethanol left in the mixture after that

$={\text{total mixture}×(\frac{(\text{total mixture – liquid removed}}{\text{total mixture}})^{\text{no of times liquid is replaced}}}$

$= 80 × (\frac{80-20}{80})^2$

$= 80 × \frac{9}{16}$

$= 45$ litres

So, water present in the final solution = 80 – 45 = 35 litres

Hence, the correct answer is option (3).

Q.5.

The average salary of male employees in a firm was Rs. 5200 and that of females was Rs. 4200. The mean salary of all the employees was Rs. 5000. What is the percentage of female employees?

1. 80%

2. 20%

3. 40%

4. 30%

Hint: Calculate ratios of male and female by the rule of alligation and find the desired value.

Required ratio = (Higher value – Mean value) : (Mean value – Lower value)

Solution:

Given: The average salary of male employees in a firm = Rs. 5200

The average salary of female employees in a firm = Rs. 4200

The average salary of all employees in a firm = Rs. 5000

By using the rule of alligation,

The ratio of the male employees to the female employees = (Higher value – Mean value) : (Mean value – Lower value)

= 800 : 200 = 4 : 1

So, the required percentage of female employees $=\frac{1}{(1+4)} × 100 = 20$%

Hence, the correct answer is option (2).

Q.6.

A bottle is filled with liquid, of which 4 parts are water and 5 parts are fruit extract. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half fruit extract?

1. $\frac{1}{10}$

2. $\frac{9}{10}$

3. $\frac{4}{9}$

4. $\frac{5}{9}$

Hint: When $x$ is a part of the mixture that has drawn off and $v$ is the total volume, then,

Final volume = Initial volume × $(1-\frac{x}{v})^n$, where $n$ = number of replacements.

Solution:

Let $x$ be a part of the mixture that has drawn off and $v$ be the total volume.

Given: Initial ratio = Water : fruit extract = 4 : 5

Final ratio = water : fruit extract = 1 : 1

Taking the volume of fruit extract, we get:

Final volume = initial volume × $(1-\frac{x}{v})^n$

⇒ $\frac{1}{2}$ = $\frac{5}{9}(1-\frac{x}{v})^1$

⇒ $\frac{9}{10}$ = $1-\frac{x}{v}$

⇒ $\frac{x}{v}$ = $\frac{1}{10}$

⇒ $x$ = $\frac{1}{10}v$

Hence, the correct answer is option (1).

Q.7.

A vessel is filled with liquid, 3 parts of which are water and 5 parts syrup. How much of the mixture must be drawn off and replaced with water so that the mixture may be half water and half syrup?

1. $\frac{1}{3}$

2. $\frac{1}{4}$

3. $\frac{1}{5}$

4. $\frac{1}{7}$

Hint: Solve by assuming that $x$ litre liquid is to be replaced.

Quantity of water in $x$ litre of liquid $=\frac{3x}{8}$

Quantity of syrup in $x$ litre of liquid $=\frac{5x}{8}$

Solution:

Given: Suppose the vessel initially contains 8 litres of liquid.

In this liquid, water is 3 litres and syrup is 5 litres.

So the ratio is $3:5$.

Let $x$ litres of this liquid be replaced with water.

Quantity of water in $x$ litre of liquid $=\frac{3x}{8}$

Quantity of syrup in $x$ litre of liquid $=\frac{5x}{8}$

As per given condition,

The quantity of water in the new mixture is $=3-\frac{3x}{8}+x$

The quantity of syrup in the new mixture is $=5-\frac{5x}{8}$

After replacement, the quantity should be the same.

$3-\frac{3x}{8}+x=5-\frac{5x}{8}$

⇒ $\frac{5x}{8}-\frac{3x}{8}+x=2$

⇒ $\frac{10x}{8}=2$

$\therefore x=\frac{8}{5}$

So, part of the mixture replaced $=\frac{\frac{8}{5}}{8}=\frac{8}{5}×\frac{1}{8}=\frac{1}{5}$

Hence, the correct answer is option (3).

Q.8.

Rice worth Rs.126 per kg and Rs.135 per kg are mixed with a third variety in the ratio of $1:1:2$. If the mixture is worth Rs.153 per kg, then the price of the third variety per kg (in Rs.) is:

1. 182.5

2. 195.5

3. 133.5

4. 175.5

Hint: Find the average price of the first and second varieties. Then, use the rule of alligation.

Solution:

The first and second varieties are mixed in equal proportions.

Their average price = $\frac{126 + 135}{2}$ = Rs.130.50

So, the mixture is formed by mixing two varieties, one at Rs. 130.50 per kg and the other at Rs.$x$ per kg, in the ratio $2:2=1:1$.

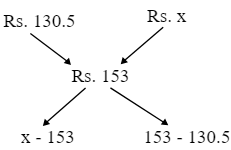
By the rule of allegation, we have,

Ratio = (Higher value – Mean value) : (Mean value – Lower value)

⇒ $\frac{1}{1} = \frac{x – 153}{153 - 130.5}$

⇒ $1 = \frac{x – 153}{22.5}$

⇒ $x = 153 + 22.5$

$\therefore x = 175.5$

Hence, the correct answer is option (4).

Q.9.

The average of marks obtained by 100 candidates in a certain examination is 30. If the average marks of the passed candidates are 35 and those of the failed candidates are 10. What is the number of candidates who passed the examination?

1. 60

2. 70

3. 80

4. 90

Hint: You have to make the ratio of pass and fail students to get the answer. Use the alligation rule.

Solution:

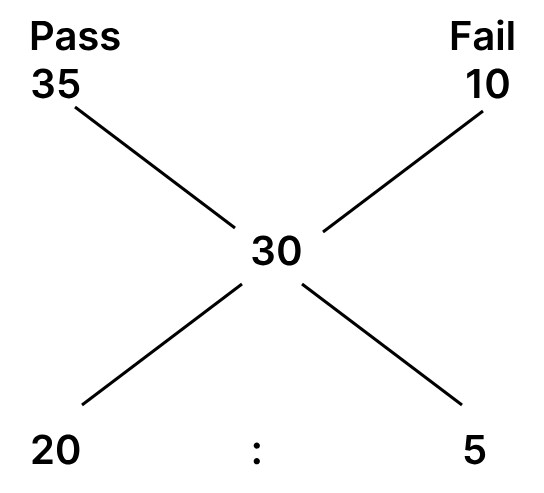
The average marks of the passed candidates are 35 and those of the failed candidates are 10.

Using the alligation method, we get,

The ratio of the number of pass students to fail students = $20:5$ = $4:1$

So, Total students = 4 + 1 = 5 units

According to the question, 5 units = 100

⇒ 1 unit = 20

Passed candidate = 4 units = 4 × 20 = 80

Hence, the correct answer is option (3).

Q.10.

A vessel is filled with liquid, 5 parts of which are water and 11 parts syrup. What part of the mixture must be drawn off and replaced with water so that the mixture may be syrup and water in the ratio $3:2$?

1. $\frac{14}{45}$

2. $\frac{27}{35}$

3. $\frac{36}{65}$

4. $\frac{7}{55}$

Hint: Let $x$ amount of liquid be replaced by water then find the ratio of syrup and water after replacement and equate them with $3:2$.

Solution:

5 parts water and 11 parts syrup (considering the unit volume of the mixture)

Water = $\frac{5}{16}$ and syrup = $\frac{11}{16}$

Let $x$ amount of liquid is replaced by water.

Water = $\frac{5x}{16}$ and syrup = $\frac{11x}{16}$

According to the question,

$\frac{\frac{11}{16}-\frac{11x}{16}}{\frac{5}{16}+x-\frac{5x}{16}}=\frac{3}{2}$

Or, $\frac{\frac{11}{16}-\frac{11x}{16}}{\frac{5}{16}+\frac{11x}{16}}=\frac{3}{2}$

Or, $\frac{15}{16}+\frac{33x}{16}=\frac{22}{16}-\frac{22x}{16}$

Or, $33x+22x=22-15$

Or, $x=\frac{7}{55}$

Hence, the correct answer is option (4).