Mode of Grouped and Ungrouped Data: An Overview

Mode is a very essential part of statistical analysis and it is a measurement part of central tendency. The mode of data set consists of two parts, The mode of ungrouped data set and the mode of grouped data set. The mode of grouped data formula derivation includes working with class intervals and modal class(which is the class interval with the highest frequency in the data set).

In this chapter, we will discuss the “mode of grouped data with unequal class sizes”, “mode of grouped data formula derivation”, “mode of grouped data with two modal class”, “mode of grouped data formula class 10”, “mode of grouped data calculator”, “mode of ungrouped data formula”, “mode of ungrouped data calculator”.

We will also practice the mode of ungrouped data questions and mode of grouped data ppt.

Also, you need to understand the terms: mode of grouped data meaning,

mode of ungrouped data definition, mode of ungrouped data set, mode of ungrouped data class 10, mode of ungrouped data example problems, mode of grouped data with two modal class

What is Mode?

The most frequent or common value in a dataset is called mode.

It is a measurement part of central tendency.

Mode is used for numerical and categorical data, unlike mean or median, which were only used for numerical data.

A dataset can have different types of modes like one mode, two modes or no mode at all.

How to Calculate the mode for Ungrouped data?

Calculating the mode of ungrouped data required some steps.

Those steps are:

Step 1: For numerical data, we have to arrange the dataset in ascending or descending order. It is an optional step. But if you apply this step, you can easily identify the mode of the data.

Step 2: Then, we have calculated the frequency of the numbers in the dataset.

Step 3: The most common or frequently used value of the dataset is called mode.

The mode of ungrouped data can be different types.

• Unimodal or single mode

• No mode

• Multimodal or multiple modes

• Catergorical mode

Unimodal or single mode:

There will be only one mode in the dataset.

Example: In the dataset, 1, 2, 3, 2, 2, the most common value is 2. (repeats 3 times)

So, the mode of the dataset is 2.

No mode:

There will be no mode in the dataset. That means the frequency of all the values in the dataset will be equal.

Example: In the dataset, 1, 2, 3, 4, and 5, there are no values which repeat.

So, there will be no mode in the dataset.

Multimodal or multiple modes:

There will be more than one mode in the dataset. That means one than one value will have the same frequency or be repeated same time.

Example: In the dataset, 1, 1, 1, 2, 3, 2, 3, 3, 4, the most common values are 1 and 3. (both repeat 3 times)

So, the mode of the dataset is 1 and 3.

Categorical mode:

The mode of this dataset is categorical.

Example: In the dataset, blue, blue, red, yellow, green, red, and black, the most common values are blue and red. (both repeat 2 times)

So, the mode of the dataset is blue and red.

How to calculate the mode for Grouped data?

Calculating the mode for the grouped data involves finding the modal class—the class interval with the highest frequency.

It involves some steps.

Those steps are:

Step 1: Identify the modal class. Modal class is the class interval with the highest frequency.

Step 2: Find the mode using the following formula.

Mode = $l + (\frac{f_1-f_0}{2f_1-f_0-f_2})×h$,

Where

the frequency of the modal class =$f_1$,

frequency of the preceding modal class = $f_0$,

frequency of the succeeding modal class = $f_2$,

class size = $h$,

lower limit of the modal class = $l$

Let's take an example to understand it better.

In this table, the modal class is 20-30, as it has the highest frequency 12.

Now, l = lower limit of the modal class = 20

h = class size = 20 - 10 = 10

f1 = the frequency of the modal class = 12

f2 = frequency of the succeeding modal class = 6

f0 = frequency of the preceding modal class = 8

Mode = $l + (\frac{f_1-f_0}{2f_1-f_0-f_2})×h = 20+(\frac{12-8}{2×12-8-6})×10=20+4$ = 24

Difference between Mean, mode, median

Suppose 2, 5, 6, 7, 5, 9, 8 is a dataset.

The mean of this data set is:

$\frac{\text{Sum of all the Observations}} {\text{Total number of Observations}}$

= $\frac{2+5+6+7+5+9+8}{7}$

= $\frac{42}{7}$

= 6

Dataset in ascending order: 2 5 5 6 7 8 9

The median of the data set is 6. (the exact middle value)

The mode of the dataset is 5 as it is twice in the dataset. (the most common value)

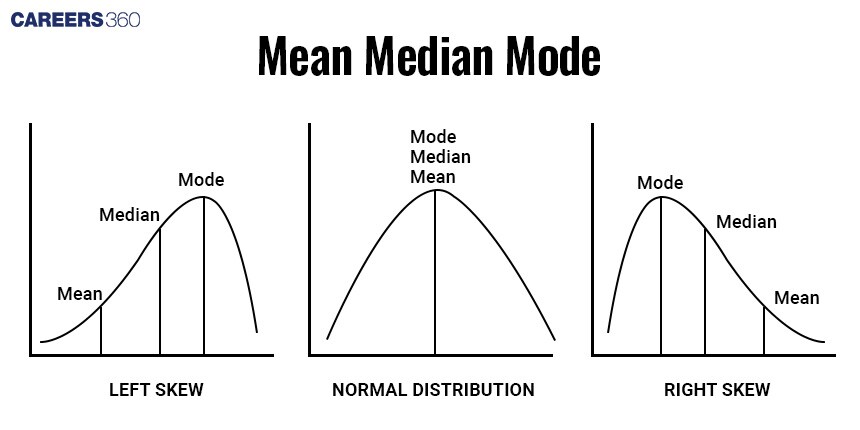
Relation between Mean, mode, median: Empirical formula

The Empirical relationship between the three measures of central tendency is

Mode = 3 × Median – 2 × Mean

This formula can be written in terms of Mode and Median

Mean = $\frac{\text{3 × Median – Mode}}{2}$

This formula can be written in terms of Mode and Mean

Median = $\frac{\text{Mode + 2 × Mean}}{3}$

Example:

Consider the data set where the mean is 50 and the median is 48. Calculate the mode.

Mode = 3 × Median – 2 × Mean = 3 × 48 – 2 × 50 = 144 – 100 = 44

More Detailed Information

To learn more about Average or Arithmetic mean, read the below article.

Average

To learn more about the mean of grouped and ungrouped data, read the below article.

Mean

To learn more about the median of grouped and ungrouped data, read the below article.

Median

Important points

• Mode is the most appearing data in a given dataset.

• Mode = (3 Median – 2 Mean)

• Mode = $l + (\frac{f_1-f_0}{2f_1-f_0-f_2})×h$, where frequency of the modal class =$f_1$, frequency of the preceding modal class = $f_0$, frequency of the succeeding modal class = $f_2$, class size = $h$, lower limit of the modal class = $l$

Practice Questions

Q1. The mode of the following data is __________.

13, 15, 31, 12, 27, 13, 27, 30, 27, 28 and 16

1. 28

2. 27

3. 30

4. 31

Hint: Mode is the most appearing data in a given dataset.

Answer:

Mode is the most appearing data in a given dataset.

Given dataset: 13, 15, 31, 12, 27, 13, 27, 30, 27, 28 and 16

Here, 27 appears 3 times, which is the most.

So, the mode is 27.

Hence, the correct answer is 27.

Q2. For a sample data, mean = 60 and median = 48. For this distribution, the mode is:

1. 18

2. 48

3. 36

4. 24

Hint: Mode = (3 Median – 2 Mean)

Answer:

Given: Mean = 60 Median = 48

We know, Mode = (3 Median – 2 Mean)

⇒ Mode = (3 × 48) – (2 × 60)

⇒ Mode = 144 – 120

$\therefore$ Mode = 24

Hence, the correct answer is 24.

Q3. Find the mode for the given distribution (rounded off to two decimal places).

1. 35.25

2. 40.25

3. 30.33

4. 28.33

Hint: Mode = $l + (\frac{f_1-f_0}{2f_1-f_0-f_2})×h$, where frequency of the modal class =$f_1$, frequency of the preceding modal class = $f_0$, frequency of the succeeding modal class = $f_2$, class size = $h$, lower limit of the modal class = $l$

Answer:

Here, the maximum frequency is 11, and the corresponding class is 25–30.

So the modal class is 25–30.

Now lower limit of the modal class ($l$) = 25,

Frequency of the modal class ($f_1$) = 11

Frequency of the preceding modal class ($f_0$) = 9

Frequency of the succeeding modal class ($f_2$) = 10

class size ($h$) = 5

We know, mode = $l + (\frac{f_1-f_0}{2f_1-f_0-f_2})×h$

= $25 + (\frac{11-9}{2(11)-9-10})×5$

= $25 + (\frac{2}{3})×5$

= $25 + 3.33$

= $28.33$

Hence, the correct answer is 28.33.

Q4. The following table represents the grouped data for the ages of a sample of people. What is the mode age group?

1. 20-30

2. 30-40

3. 50-60

4. 60-70

Answer:

The highest frequency age group must be found to determine the mode for grouped data because it serves as the mode. In this instance, 50-60 has the largest frequency of age groups with 23 people.

Hence, the correct answer is 50-60.

Q5. In a frequency distribution table, the mode is:

1. The value in the class with the highest frequency.

2. The value in the first class.

3. The value in the last class.

4. The average of all data values.

Answer:

The value inside the class (interval) with the highest frequency is referred to as the mode in a frequency distribution table. It stands for the dataset's most prevalent value or category. The class with the highest frequency is used to determine the mode, which is then commonly regarded to be the midpoint of that class.

Hence, the correct answer is 'The value in the class with the highest frequency'.

Q6. What is the mode of the ungrouped data: $18,22,25,18,21,22,22,25,18,25$

1. 18

2. 22

3. 25

4. All of the above

Answer:

The values with the highest frequency are 18, 22, and 25, so this dataset is multimodal, and the modes are options A) 18, B) 22, and C) 25.

Hence, the correct answer is 'All of the above'.

Q7. What is the mode of the given data?

5, 7, 9, 7, 3, 7, 5, 7, 8, 6, 7

1. 7

2. 6

3. 5

4. 3

Hint: Mode is the most frequently appeared observation in the given data.

Answer:

Given: 5, 7, 9, 7, 3, 7, 5, 7, 8, 6, 7

In the given data 7 appears 5 times, which is the highest.

So, mode = 7

Hence, the correct answer is 7.