Number of factors and Number of Trailing Zeros - How to Find, Examples

In Mathematics, the number of factors and trailing zeroes in large numbers and factorials is a very important chapter for solving a wide range of problems.

Integers that can be multiplied together to produce the original number are called Factors of a number.

In other words, if you have a number n, then any integer d that divides n without leaving a remainder is called a factor of n.

The number of consecutive zeros at the end of the number is called the number of trailing zeros of a number.

Example: In 100,00 are the trailing zeroes of 100.

The prime factorization method is the most commonly used. In the Prime factorization method, we express the number as a product of prime factors.

In this chapter, we will also learn about the greatest common factor calculator and how to find the zeros of the function calculator.

Number of Factors and Sum of Factors

Let's take a natural number n. We have to find its factors.
Using the Prime factorization method, we get N = $X^a × Y^b × Z^c$,

Where X, Y, and Z are prime numbers and a, b, and c are their respective exponents.
Let us solve an example taking N = 60

Number of trailing zeros

The zeros at the end of a number are called the number of trailing zeros.
In the picture below, it is clearly explained what the zeros of a number are called in different places of a number.

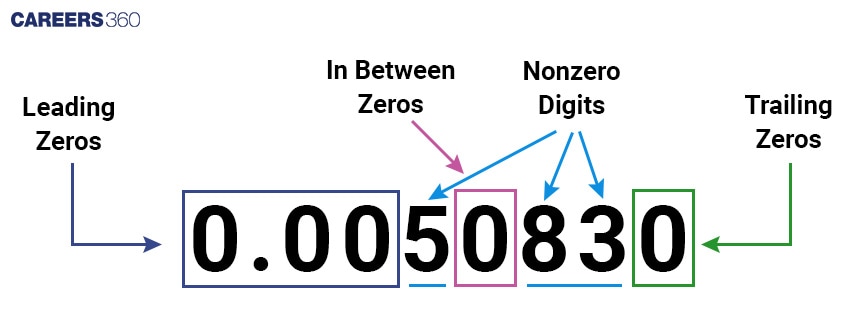
Numbers with trailing zeros

If a number is divisible by 10, then it has trailing zeros. The highest power of 10 by which that number is completely divisible will be the number of trailing zeros in that number.

Example:

100 is divisible by 10, and the highest power of 10 by which 100 is completely divisible is 2.

So, 100 has 2 trailing zeros.

Let's take more complicated examples.

• 2¹⁰ × 3⁴ × 5⁹ has how many trailing zeros?

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. Number of Factors and Sum of Factors
2. Number of trailing zeros
3. Finding the highest value of n if a can divide x completely
4. Tips and Tricks related to the number of factors and trailing zeroes
5. Practice Questions

Answer:

First, we will equal the exponents of 2 and 5.
Then we will combine them to get the power of 10.

That will be our answer.

= 2¹⁰ × 3⁴ × 5⁹

= 2⁹ × 2 × 3⁴ × 5⁹

= 10⁹ × 2 × 3⁴

So, there are 9 trailing zeros.

Find the number of trailing zeros in a Factorial

• To find the number of trailing zeros in a factorial, we must find how many times 10 is a factor of that number.

We know that 2 × 5 = 10

There are more number 2 as a factor rather than 5 in a number.

So, we need to find the number of 5’s.

• To find the number of factors of 5, we have to consider the number of multiples of 5, i.e., 25, 125, ….

We know that each multiple of 5 gives at least one 5 as a factor.

Each factor of 25 gives at least 2 factors of 5.

Each factor of 125 gives at least 3 factors of 5.

Formula

The formula to fo find the number of trailing zeros in n!

= $[\frac{n}{5}]+[\frac{n}{25}]+[\frac{n}{125}]+........$

Where [ ] is the greatest integer function which will give the integer part only as a result.

Continue this formula until n < multiple of 5

Let’s take an example.

Q. Find the trailing zeros of 30!

As 30 < 125, this formula will continue till $\frac{n}{25}$, (rounding up to nearest integer)

$\frac{30}{5}+\frac{30}{25}=6+1=7$

Hence, the number of trailing zeros in 30! is 7.

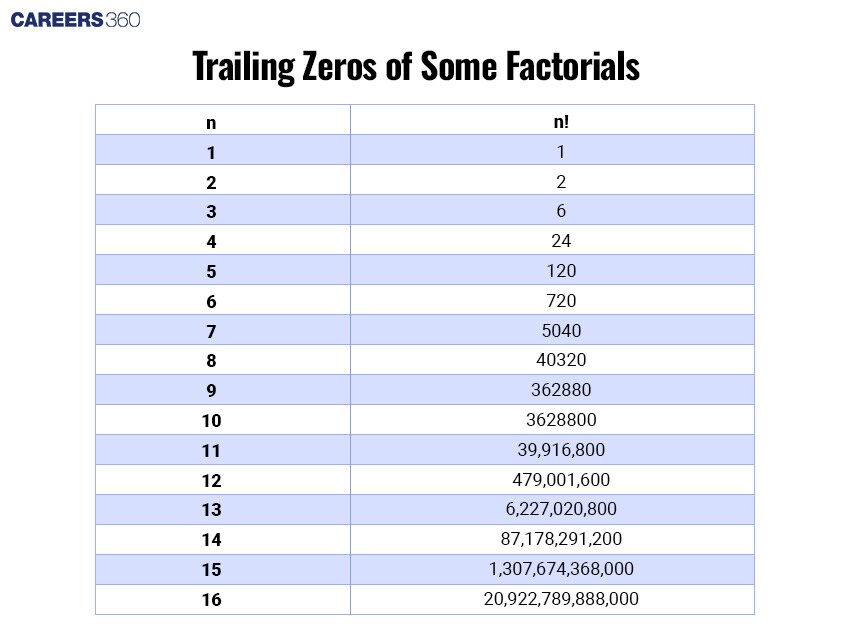
Here is a list till factorial 16. We can check that formula on this factorial too to see if the formula is right or not.

Let's take 16!

Here 16 < 25

So, formula will only go till $\frac{n}{5}$, (rounding up to nearest integer)

$\frac{16}{5}=3$

Hence, there are 3 trailing zeros in 16!

So the formula is right.

Numbers without trailing zeros

Now, there will be numbers that don't have trailing zeros. Now we will discuss them.

• Numbers that do not consist of factors of 5 will not have trailing zeros as 2 and 5 combined make zeros, which will not be possible with factors of 5.

Example: 1, 2, 4, 7, 12, etc.

• Odd numbers do not consist of 2 as a factor. So, for any powers of odd numbers, there will be no trailing zeros.

Example: 1, 3, 5, 7, etc

• Prime numbers that are neither 2 nor 5 do not have trailing zeros because they do not include both necessary factors (2 and 5).

Example: 3, 7, 11, 17, 19, etc.

Number with trailing zeros in other bases

Trailing zeroes in a number, when expressed in a given base, is determined by how many times the number can be divided by that base without leaving a remainder.

Let’s take an example to understand it better.

Suppose we have to find trailing zeros of 100! in the base of 50.

Prime factors of 50 = 2 × 5 × 5 = 21 × 52

Now, we have to how many times each prime factor appears in the factorial.

We will use the same process as how we use during finding factors of 5.

Factors of 2 in 100! = $\frac{100}{2}+\frac{100}{4}+\frac{100}{8}+\frac{100}{16}+\frac{100}{32}+\frac{100}{64}=50+25+12+6+3+1=97$ (rounding up to the nearest integer)

Factors of 5 in 100!

= $\frac{100}{5}+\frac{100}{25}=20+4=24$ (rounding up to the nearest integer)

For base 50, we need 2 factors of 5 for 1 factor of 2.

So, dividing the number of factors of 5 by 2, we get, $\frac{24}{2}=12$

Since we need 1 factor of 2 for every 52, 12 is the limiting factor here.

So, there are 12 trailing zeros in 100! base 50

Finding the highest value of n if a can divide x completely

The highest value of n if aⁿ can completely divide x, is determined by the smallest number of prime factors of a fit into the prime factors of x.

Let’s take an example to understand it step-by-step.

Suppose x = 400!

and a = 20

Now, we have to do prime factorization 20.

20 = 2 × 2 × 5 = 22 × 51

Let’s find out how many powers of 5 are in 400!

$\frac{400}{5}+\frac{400}{25}+\frac{400}{125}=80+16+3=99$ (rounding up to the nearest integer)

So, the number of 5 in 400! is 99.

Now, let's find out how many power of 2 is in 400!

$\frac{400}{2}+\frac{400}{4}+\frac{400}{8}+\frac{400}{16}+\frac{400}{32}+\frac{400}{64}+\frac{400}{128}+\frac{400}{256}=200+100+50+25+12+6+3+1=397$ (rounding up to the nearest integer)

So, the number of 22 in 400! is $\frac{397}{2}=198$ (rounding up to the nearest integer)

The smallest value from the above calculation is the highest value of n, i.e., 99.

Tips and Tricks related to the number of factors and trailing zeroes

• The number of trailing zeroes in n! (n factorial) is determined by the number of times 5 is a factor in numbers from 1 to n, as there are usually more factors of 2 than 5.

• If a number finishes with zero at the end, then the trailing zero of that number is the exponent of that number.

Example: trailing zeros of 10ⁿ is n.

• During the multiplication of several numbers, count the total number of factors of 2 and 5 in the prime factorizations of the numbers involved. The number of trailing zeros is the minimum of the number of factors of 2 and the number of factors of 5.

Practice Questions

Q1. Find the number of factors of 360.

1. 12

2. 24

3. 36

4. 48

Answer:

Prime factorisation of 360

= 360 = 2 × 2 × 2 × 3 × 3 × 5 = 23 × 32 × 51

Let a = 3, b = 2, c = 1

We know the number of all factors of a number
= (a + 1) (b + 1) (c + 1)

= (3 + 1) (2 + 1) (1 + 1)

= 24

Hence, the correct answer is 24.

Q2. Find the number of trailing zeros in 75!

1. 12

2. 18

3. 24

4. 15

Answer:

Here 75 < 125

So, the formula will go until $\frac{n}{25}$. (rounding up to the nearest integer)

$\frac{75}{5}+\frac{75}{25}=15+3=18$

Hence, the correct answer is 24.

Q3. Find the number of trailing zeros in 100!

1. 24

2. 20

3. 22

4. 30

Answer:

Here 100 < 125

So, the formula will go until $\frac{n}{25}$. (rounding up to the nearest integer)

$\frac{100}{5}+\frac{100}{25}=20+4=24$

Hence, the correct answer is 24.

Q4. What is the highest value of n for which 3n can divide 81! completely?

1. 20

2. 30

3. 40

4. 10

Answer:

Prime factorisation of 81 = 81 = 3 × 3 × 3 × 3 = 34

Let’s find out how many powers of 3 is in 81!

$\frac{81}{3}+\frac{81}{9}+\frac{81}{27}+\frac{81}{81}=27+9+3+1=40$ (rounding up to the nearest integer)

So, the number of 34 in 81! is $\frac{40}{4}=10$ (rounding up to the nearest integer)

Hence, the correct answer is 24.

Q5. Find the product of all the factors of 100.

1. $100^9$

2. $10^19$

3. $1^9$

4. $10^9$

Answer:

Prime factorisation of 100

= 100 = 2 × 2 × 5 × 5 = 22 × 52

Here, a = 2, b = 2

Number of factors of 100 = (a + 1) (b + 1) = (2 + 1) (2 + 1) = 9

We know the product of factors of 100

= $100^{\frac{\text{Total number of factors}}{2}}$

= $100^{\frac{9}{2}}$

= $(10^2)^{\frac{9}{2}}$

= $10^9$

Hence, the correct answer is $10^9$.

Q6. Find the number of even factors of 200.

1. 3

2. 6

3. 9

4. 12

Answer:

Prime factorisation of 200

= 200 = 2 × 2 × 2 × 5 × 5 = 23 × 52

Here, a = 3, b = 2

$\therefore$ Number of even factors of 200 = a (b + 1) = 3 (2 + 1) = 9

Hence, the correct answer is 9.

Q7. How many odd factors are there in 720?

1. 6

2. 30

3. 24

4. 8

Answer:

Prime factorisation of 720

= 720 = 2 × 2 × 2 × 2 × 3 × 3 × 5 = 24 × 32 × 51

To count the odd factors we will ignore the power of 2.

Then add 1 with the other two exponents and multiply them.

So, number of odd factors of 720 = (2 + 1) (1 + 1) = 6

Hence, the correct answer is 6.

Q8. Prove that the number of trailing zeros of 6!, 7!, 8! and 9! are all the same.

Answer:

Here, all the numbers are less than 25.

So, the formula to find trailing zeros of factorials will only go till $\frac{n}{5}$.

• When n = 6, $\frac{n}{5}=\frac{6}{5}=1$ (rounding up to nearest integer)

• When n = 7, $\frac{n}{5}=\frac{7}{5}=1$ (rounding up to nearest integer)

• When n = 8, $\frac{n}{5}=\frac{8}{5}=1$ (rounding up to nearest integer)

• When n = 9, $\frac{n}{5}=\frac{9}{5}=1$ (rounding up to nearest integer)

So, we can see that 6!, 7!, 8!, and 9! have same number of trailing zeros, i.e., 1.

Q9. How many trailing zeros are in this product? 27 × 94 × 55 × 33

1. 7

2. 5

3. 3

4. 4

Answer:

27 × 94 × 55 × 33

= 25 × 22 × 94 × 55 × 33

= 105 × 22 × 94 × 33

Here, the power of 10 is 5.

Hence, the correct answer is 5.

Q10. Are there the same numbers of trailing zeros in 25 × 1117 × 52 and 22 × 1711 × 55?

Answer:

25 × 1117 × 52

= 22 × 23 × 1117 × 52

= 102 × 23 × 1117

Here, the number of trailing zeros is 2.

22 × 1711 × 55

= 22 × 1711 × 53 × 52

= 102 × 53 × 1711

Here, the number of trailing zeros is 2.

So, there are the same numbers of trailing zeros in both products.