Polygon: Definition, Shape, Area Formula, Properties, Examples

Polygon is a very important chapter in Mathematics and Geometry. A polygon is a close figure created by a finite number of line segments. The polygon definition in geometry can be found in shapes like triangles, rectangles, squares, etc. About polygons and quadrilaterals, we can say that every quadrilateral is a polygon but not every polygon is a quadrilateral.

CAT 2024: 20 Free Mock Test | 10 Year PYQs | 60 Day Study Material | Most Scoring Concepts

XAT 2025: Section-wise Preparation Tips | Sample Paper

Don't Miss: SNAP 2024 Sample Papers | NMAT 2024 Sample Papers | MAT 2024 Sample Papers

This Story also Contains

1. What are Polygons?
2. Types of polygon
3. Difference Between Regular and Irregular Polygons
4. Diagonals of Polygon
5. Angles of a polygon
6. Three-dimensional shape
7. Summary of all formulae and properties
8. Tips and Tricks
9. Practice Questions

We will also discuss “polygon sides”, “polygon formula area”, “polygon definition and examples”, and “polygon properties” in this chapter.

What are Polygons?

A closed two-dimensional figure composed of a finite number of straight line segments connected end to end is called a polygon. These line segments are called the sides of a polygon. The point where two line segments meet is called corners or vertices.

Polygons can be regular or irregular.

Triangles, squares, and rectangles are some of the examples of polygon.

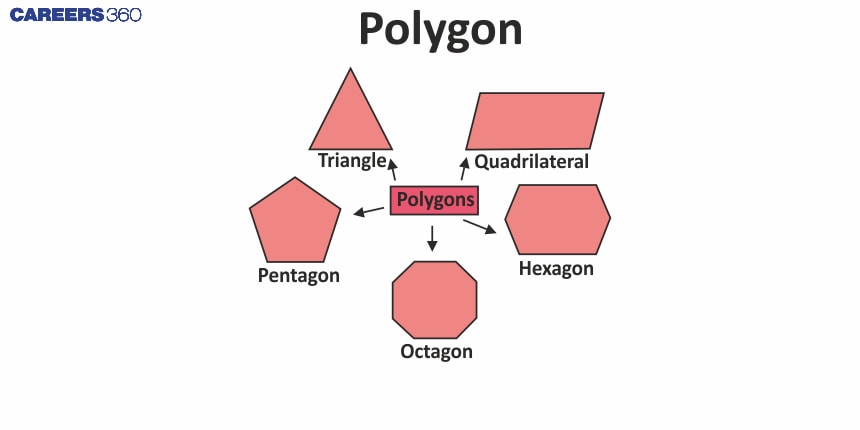
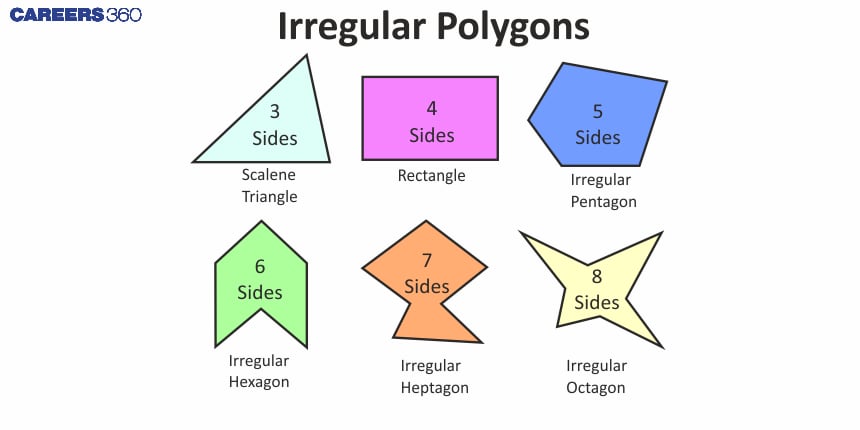
Different shapes of a Polygon

Polygons have different shapes depending on the number of sides they have.

Some of the very common shapes are:

Triangles like equilateral triangles, isosceles triangles, and scalene triangles.

Quadrilaterals like squares, rectangles, rhombuses, parallelograms and kites.

Some of the pictures of different shapes are given below.

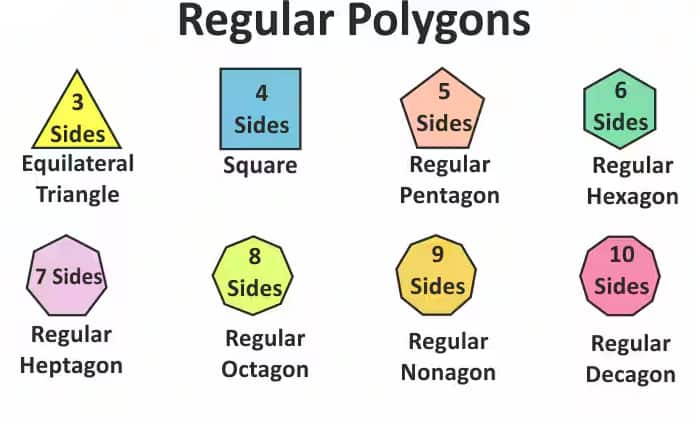
List of Polygons of sides up to 12

Types of polygon

Polygons can be categorised based on their sides and angles into several types. Here are the main types of polygons:

• Regular Polygon

• Irregular Polygon

• Convex Polygon

• Concave Polygon

Now we will discuss these types of polygons thoroughly.

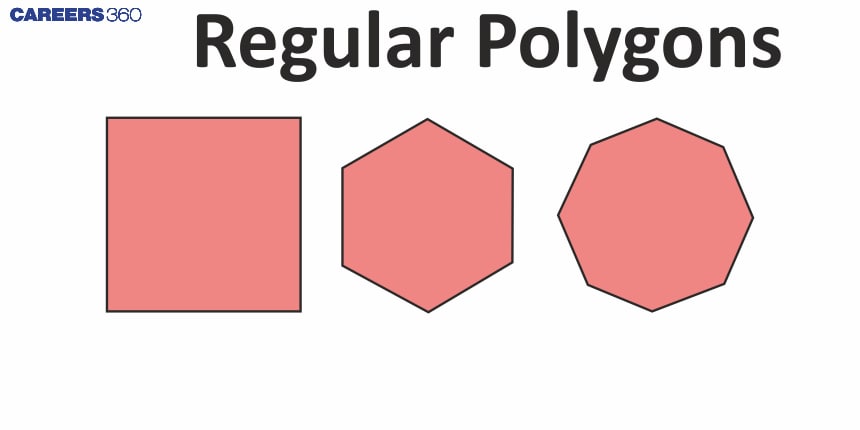
Regular polygons

A polygon with equal sides and equal angles is called a Regular polygon.

Key properties of regular polygons are:

• All interior angles are equal.

• All sides are equal in length.

• Regular polygons are symmetrical.

Some examples of regular polygons are equilateral triangles, squares, regular pentagons and regular hexagons.

Irregular polygons

A polygon with sides and angles that are not equal in length is called an Irregular polygon.

Key properties of irregular polygons are:

• All interior angles are not equal in measurement.

• All sides are not equal in length.

• Irregular polygons are not symmetrical.

Some examples of irregular polygons are scalene triangles, irregular pentagons and irregular hexagons.

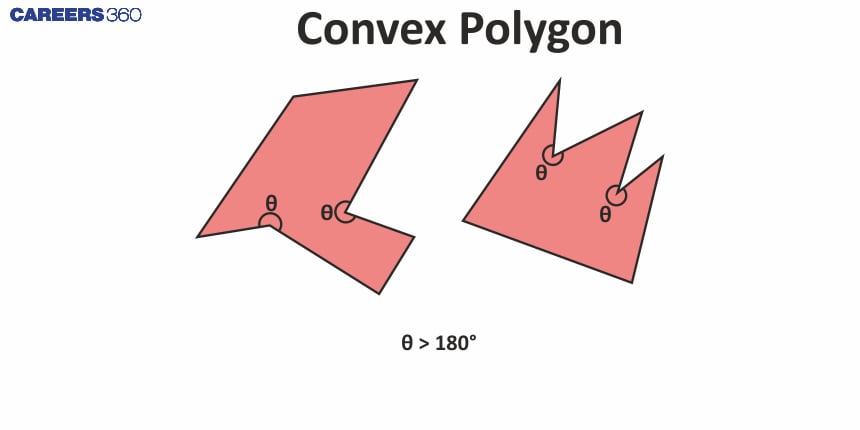
Convex polygons

A polygon with interior angles less than 180° is called a Convex polygon. In these polygons, no vertices point inwards.

Key properties of Convex polygons are:

• All diagonals lie inside the polygon.

• No line segment between two vertices goes outside the polygon.

Some examples of Convex polygons are equilateral triangles, squares, and other polygons where interior angles are less than 180°.

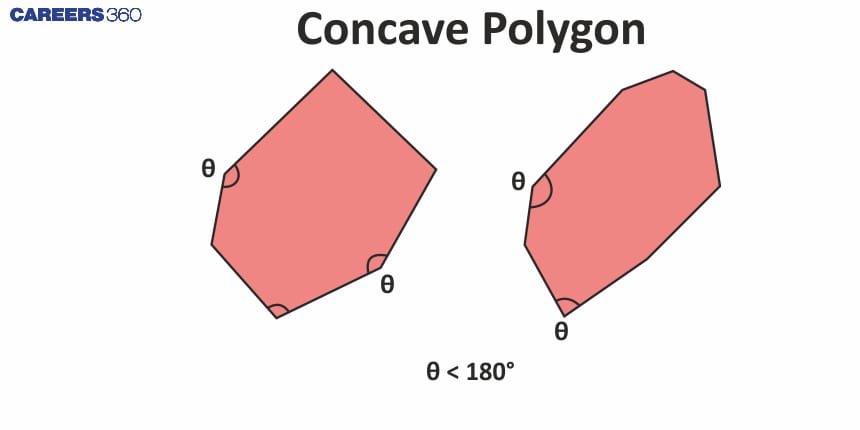
Concave polygons

A polygon with at least one interior angle greater than 180° is called a Concave polygon. In these polygons, at least one vertex points inward.

Key properties of Concave polygons are:

• At least one diagonal lies outside the polygon.

• A line segment between two vertices can go outside the polygon.

Some examples of Concave polygons are star-shaped polygons and some irregularly shaped polygons.

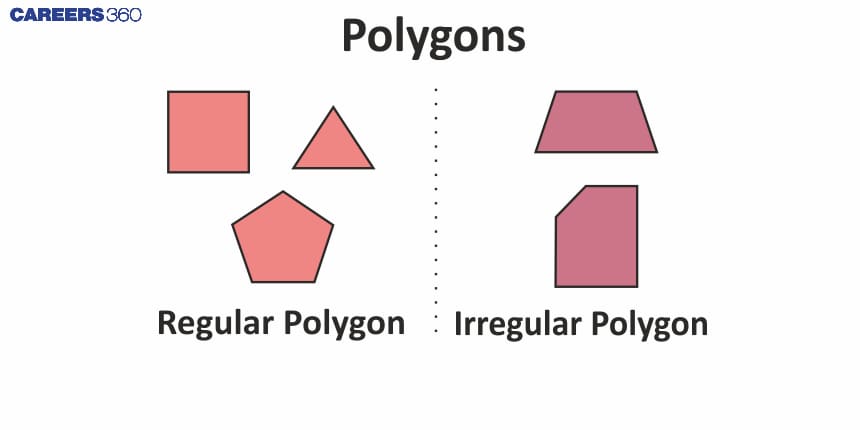
Difference Between Regular and Irregular Polygons

A polygon can be categorized as a regular or irregular polygon based on the length of its sides and the measure of its angles. The difference between a regular and irregular polygon is given in the following table.

Diagonals of Polygon

A line segment that connects two non-adjacent vertices is called the diagonals of a polygon. The number of diagonals increases as the number of sides increases.

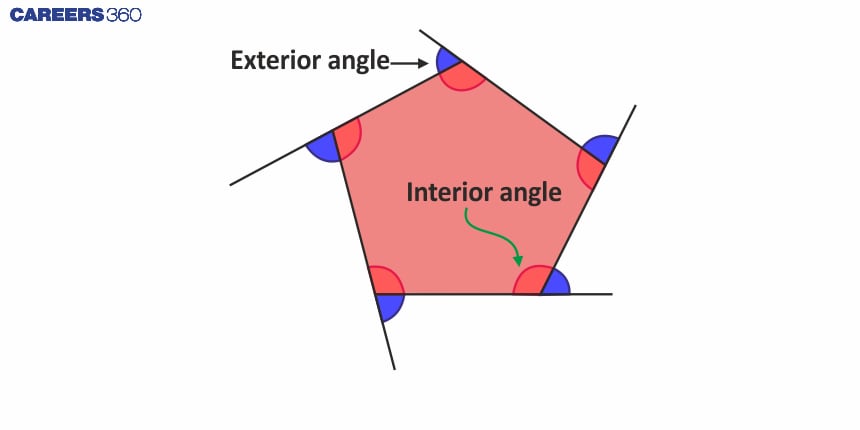
Angles of a polygon

Polygons have two types of angles.

• Interior angles

• Exterior angles

Interior angles:

Angles formed by two adjacent sides inside of a polygon are called interior angles.

Exterior angles:

Angles on the outside of a polygon, are formed by extending one side of the polygon, called Exterior angles.

Interior angle sum formula

The sum of interior angles depends on the number of sides.

Suppose the number of sides in a polygon is n.

Then the sum of the interior angles in that polygon is:

(n – 2) × 180°

All interior angles of a regular polygon are equal. If we divide the sum of the interior angles of a polygon by the number of sides of that polygon, we get the measurement of each interior angle.

So, the formula to find each interior angle of a polygon is:

$\frac{(n - 2)}{n}$ × 180°, where n = number of sides

Example:

Find the sum of the measures of all the interior angles of a polygon having twelve sides.

A polygon with $n$ sides has an interior angle sum = $(n -2)×180°$

= $(12 - 2)×180°$

= $10×180°$

= $1800°$

Hence, the correct answer is 1800°.

Exterior angle of a polygon

An angle formed between one side of the polygon and the extension of its adjacent side is called the Exterior angle of a polygon.

For any polygon, the sum of exterior angles is always 360°.

In a regular polygon, all exterior angles are equal. If we divide the sum of the exterior angles of a polygon by the number of sides of that polygon, we get the measurement of each exterior angle.

So, the formula to find each interior angle of a polygon is:

$\frac{360°}{n}$, where n = number of sides

Example:

In a regular hexagon, find the measurement of each exterior angle.

In a hexagon, number of sides = 6

The sum of exterior angles is 360°.

$\therefore$ Each exterior angle = $\frac{360°}{6}$ = 60°

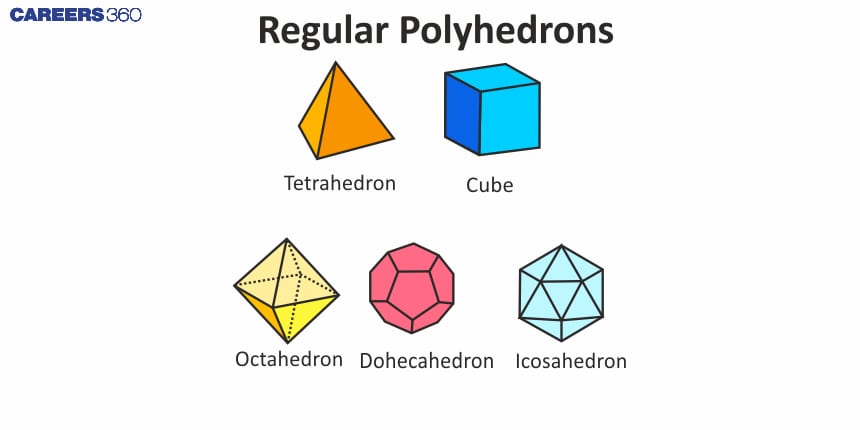
Three-dimensional shape

In general, polygons are two-dimensional figures with straight-line segments that form a closed shape.

But a three-dimensional shape whose face is a polygon is called a Polyhedron. More than one polyhedron is called Polyhedra.

Properties of Polyhedron are:

• Vertices are the points where edges meet.

• Edges are the line segments where two faces meet.

• Faces are flat-surfaced polygons.

Examples of polyhedra are cubes, rectangular or triangular prism and pyramids.

Summary of all formulae and properties

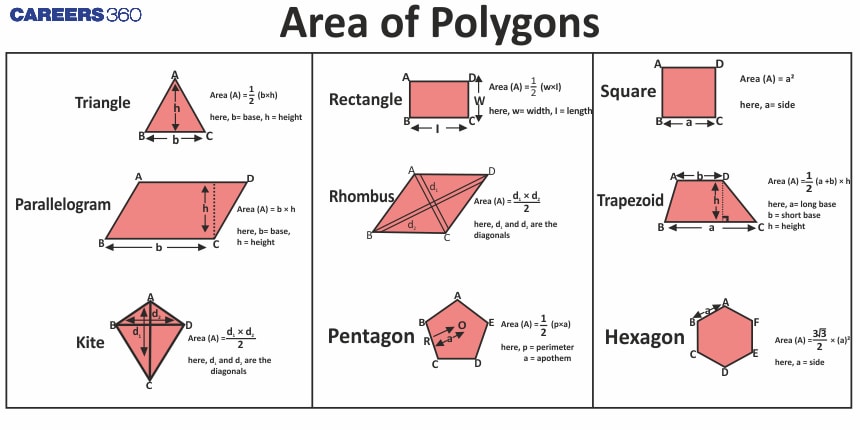
Summary of all formulae related to areas of various types of polygons

Tips and Tricks

• Exterior angle of a polygon = $\frac{360°}{\text{number of sides}}$

• Number of sides of polygon = $\frac{360°}{\text{each exterior angle}}$

• Number of diagonals = $\frac{n(n-3)}{2}$, where $n$ = sides of polygon

• The sum of interior angles = (n - 2) × 180°, where n = number of sides of a polygon

• The area of the regular hexagon of side $a$ is $6\times \frac{\sqrt3}{4}a^2$.

Practice Questions

Q1. If the external angle of a regular polygon is 18°, then the number of diagonals in this polygon is:

1. 180

2. 170

3. 150

4. 140

Hint: Number of sides of polygon = $\frac{360°}{\text{each exterior angle}}$

Number of diagonals = $\frac{n(n-3)}{2}$, where $n$ = sides of polygon

Answer:

Given,

Each exterior angle of a polygon is 18°.

We know that the sum of the exterior angles of a polygon is 360°.

Number of sides of polygon = $\frac{360°}{\text{each exterior angle}}$

⇒ Number of sides of regular polygon, $n$ = $\frac{360°}{18°} = 20$

$\therefore$ Number of diagonals = $\frac{n(n-3)}{2}=\frac{20(20-3)}{2}=170$

Hence, the correct answer is 170.

Q2. There are two regular polygons with numbers of sides equal to $(n-1)$ and $(n+2)$. Their exterior angles differ by 6°. The value of $n$ is:

1. 14

2. 12

3. 11

4. 13

Hint: Use the formula: Exterior angle of a polygon = $\frac{360°}{\text{number of sides}}$

Answer:

Given: There are two regular polygons with numbers of sides equal to ($n$–1) and ($n$+2). Their exterior angles differ by 6°.

We know that exterior angle of a polygon = $\frac{360°}{\text{number of sides}}$

According to the question,

$\frac{360°}{n-1}-\frac{360°}{n+2}=6°$

$⇒360°(\frac{1}{n-1}-\frac{1}{n+2})=6°$

$⇒60°[\frac{n+2-n+1}{(n-1)(n+2)}]=1$

$⇒n^2+n-2=180$

$⇒n^2+n-182=0$

$⇒(n+14)(n-13)=0$

$\therefore n=13$ (Since $n$ can't be negative)

Hence, the correct answer is 13.

Q4. How many diagonals are there in an octagon?

1. 12

2. 14

3. 20

4. 24

Hint: The number of the diagonals in a $n$ sided polygon is given as $\frac{n(n–3)}{2}$.

Answer:

Given: Number of sides of an octagon, $n=8$.

The number of the diagonals in a $n$ sided polygon is given as $\frac{n(n–3)}{2}$.

Number of diagonals of an octagon

= $\frac{8(8–3)}{2}$

= 20

Hence, the correct answer is 20.

Q4. If one of the interior angles of a regular polygon is $\frac{15}{16}$ times of one of the interior angles of a regular decagon, then find the number of diagonals of the polygon.

1. 20

2. 14

3. 2

4. 35

Hint: Use the formula:

⇒ Interior angle of a regular polygon = $\frac{(n-2)×180^{\circ}}{n}$

⇒ Number of diagonals = $\frac{n(n-3)}{2}$

Where $n$ is the number of edges.

Answer:

Interior angle of a regular polygon = $\frac{(n-2) \times180^{\circ}}{n}$

Interior angle of a regular decagon = $\frac{(10-2) \times180^{\circ}}{10}$ = $144^{\circ}$

Interior angle of a regular polygon = $\frac{15}{16}×144^{\circ}$ = $135^{\circ}$

⇒ $\frac{(n-2) \times 180^{\circ}}{n}$ = $135^{\circ}$

⇒ $180n - 135n$ = $360$

⇒ $n$ = $\frac{360}{45}$ = 8

Number of diagonals = $\frac{n(n-3)}{2}$ = $\frac{8(8-3)}{2}$ = 20

Hence, the correct answer is 20.

Q5. The length and breadth of a rectangle are 8 cm and 6 cm, respectively. The rectangle is cut on its four vertices such that the resulting figure is a regular octagon. What is the length of the side (in cm) of the octagon?

1. $3\sqrt{11}-7$

2. $5\sqrt{13}-8$

3. $5\sqrt{7}-11$

4. $6\sqrt{11}-9$

Hint: Let the sides of the octagon be $a$ cm, then use the Pythagoras theorem (Hypotenuse2 = Base2 + Perpendicular2) to make an equation.

Answer:

Given: The length and breadth of a rectangle are 8 cm and 6 cm, respectively. The rectangle is cut on its four vertices such that the resulting figure is a regular octagon.

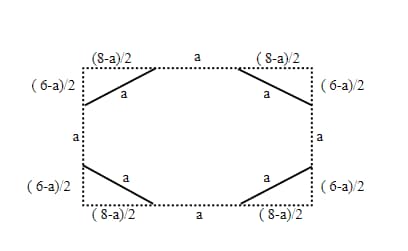
Let the sides of the octagon be $a$ cm.

From the figure, we get,

$a^2=\frac{(8–a)^2}{4}+\frac{(6–a)^2}{4}$

⇒ $a^2=16-4a+\frac{a^2}{4}+9-3a+\frac{a^2}{4}$

⇒ $a^2=\frac{a^2}{2}+25-7a$

⇒ $a^2+14a-50=0$

Solving this, we get,

$a=(3\sqrt{11}-7)$ cm

Hence, the correct answer is $3\sqrt{11}-7$.

Q6. ABCDEF is a regular hexagon. The side of the hexagon is 36 cm. What is the area of the $\triangle ABC$?

1. $324 \sqrt{3}$ cm2

2. $360 \sqrt{3}$ cm2

3. $240 \sqrt{3}$ cm2

4. $192 \sqrt{3}$ cm2

Hint:

The area of the regular hexagon of side $a$ is $6\times \frac{\sqrt3}{4}a^2$.

Answer:

Given: ABCDEF is a regular hexagon.

The side of the hexagon is 36 cm.

The area of the regular hexagon of side $a$ is $6\times \frac{\sqrt3}{4}a^2$.

A regular hexagon is divided into six equal triangles.

So, the area of the $\triangle ABC$ $=\frac{1}{6}\times 6\times \frac{\sqrt3}{4}a^2$.

⇒ $\frac{1}{6}\times 6\times \frac{\sqrt3}{4}\times (36)^2=324 \sqrt3$ cm2

Hence, the correct answer is $324\sqrt3 $ cm2.

Q7. PQRS is a square whose side is 16 cm. What is the value of the side (in cm) of the largest regular octagon that can be cut from the given square?

1. $8-4\sqrt2$

2. $16+8\sqrt2$

3. $16\sqrt2-16$

4. $16-8\sqrt2$

Hint: In a right-angled triangle, Hypotenuse2 = Base2 + Perpendicular2

Answer:

Given: PQRS is a square whose side is 16 cm.

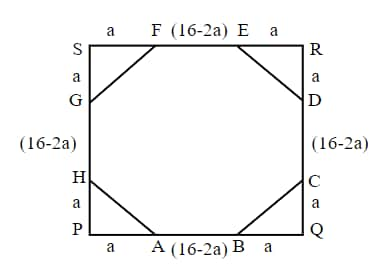
Let ER = RD = $a$ cm

So, the sides of the octagon ED = CD = (16 – 2a) cm

From $\triangle$ERD,

$(16-2a)^2=a^2+a^2$

⇒ $256-64a+4a^2=2a^2$

⇒ $2a^2-64a+256=0$

⇒ $a^2-32a+128=0$

Solving this we get,

⇒ $a = \frac{-(-32)+\sqrt{(32^2 -4×128)}}{2}$

⇒ $a=16-8\sqrt2$ cm

So, the sides of the octagon = $16-2(16-8\sqrt2)=16\sqrt2-16$ cm

Hence, the correct answer is $16\sqrt2-16$.

Q8. If the sum of the measures of all the interior angles of a polygon is 1440$^\circ$, find the number of sides of the polygon.

1. 8

2. 12

3. 10

4. 14

Hint: A polygon with $n$ sides has an interior angle sum of $(n – 2)×180^\circ$.

Answer:

Given: If the sum of the measures of all the interior angles of a polygon is 1440$^\circ$.

A polygon with $n$ sides has an interior angle sum of $(n – 2)×180^\circ$.

According to the question,

$(n – 2)×180^\circ=1440^\circ$

⇒ $n–2=8$

⇒ $n=10$

Hence, the correct answer is 10.