Probability: Definition, Formula, Sampling, Algebra Event, Theory

Probability is a useful topic in our daily life. It can provide us with the chance of an event happening or not. The probability formula, probability distribution, probability of grouped data, probability density function, probability in statistics, probability definition, probability sampling methods, probability theory, and probability algebra event are some of the important topics of probability. We are going to explore how to solve any probability-related problems and all the related topics in this article.

Also, understand the terms like algebra events and probability of multiple events algebra 2.

Also, read probability for data science pdf, probability of multiple events algebra 2, probability of an event definition math, probability of 4 events, algebra of events in probability pdf.

Probability: An Overview

Probability is the actual likelihood of any event or any situation to occur. For example, if we toss a coin the probability of getting a head is 50% or $\frac{1}{2}$. The application of probability is vast in many of our real-life scenarios. In games, we predict the probability of any team losing or winning, We also use probability whenever we talk about how the weather is going to be.

What is Probability?

Probability is a measure of how likely an event is to happen. With the help of probability, we can predict the chance of an event to occur. The value of probability ranges between 0 to 1, where 0 represents the impossible event and 1 represents the probability of events that are certain to happen.

Terms used in Probability

• Sample Space: All the possible outcomes of an experiment together make up a sample space. For example, the sample space for a coin toss is {Heads, Tails}.

• Outcome and Trial: A trial means doing or performing an experiment and an outcome is the result of that experiment. For example, if rolling a dice is a trial then getting a 3 is an outcome.

• Event: An event is some of the specific outcomes of an experiment, in other words, an event is a subset of the sample space.

• Favourable Event: Favourable events are those events associated with the experiment which are of interest to us. When rolling a dice if we are interested in even numbers then getting a 2 is called favourable event.

• Non-favorable Event: Non-favourable events are those events associated with the experiment in which we are not interested. When rolling a die if we are interested in even numbers then getting a 3 is called a non-favourable event.

• Exhaustive Events: Exhaustive events are all those events that take up all the possible outcomes of an experiment. When rolling a die the exhaustive events are getting a 1, 2, 3, 4, 5, and 6.

• Mutually Exclusive Events: When some events can not happen at the same time or simultaneously, then they are called mutually exclusive events. When tossing a coin getting head or tail are mutually exclusive events.

• Independent Events: Independent events are those events where the occurrence of one event does not affect the other event's occurrence or vice versa. For example, flipping a coin and rolling a die can be considered independent events.

• Impossible Events: An impossible event is an event which cannot happen. For example, rolling a 7 on a standard six-sided die is an impossible event.

Formula of Probability

The probability of an event A is written as P(A), and it can easily calculated using the formula:

P(A) = $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$

For example, while rolling a dice probability of getting a 6 is $\frac{1}{6}$.

What is the probability of an Impossible event?

The probability of an impossible event is always 0, as it can not happen under any situation. If you roll a standard six-sided die, it is impossible to get a 7, as there is no 7 on the die. So in this case the probability of rolling a 7 is 0.

What is the probability of a sure event?

The probability of a sure event is always 1 because it is certain to occur. When we flip a coin, we are certain to get a head or a tail, so getting a head or a tail in this case is a sure event. Hence, the probability of getting either heads or tails is 1, when we toss a coin.

Formula of Probability in Different Conditions

Probability if either of the two events occurred (Addition Rule)

The probability when either of two events occurred or the addition rule states that the probability of either of the two events occurring is the sum of their individual probabilities minus the probability of both events happening. The formula is:

P(A $\cup$ B) = P(A) + P(B) - P (A $\cap$ B)

Where P(A $\cup$ B) is the probability of either event A or event B occurring.

P(A∩B) is the probability of both events A and B occurring.

P(A) is the probability of event A occurring.

P(B) is the probability of event B occurring.

Probability of Complementary event

Complementary events in probability are two such events which are mutually exclusive events which means they can not happen together, in other words, if one event occurs then the other event can not occur. The sum of the probability of two complementary events is 1. The formula:

P(A′) = 1 - P(A)

where P(A) is the probability of the event A, and P(A′) is the probability of the event A′ (the complement of A).

Conditional Probability (Probability of B if A has already occurred)

Conditional probability is the probability of an event B occurring given that another event A has already happened. It is denoted by P(B∣A) and it is calculated using the formula:

$P(B∣A) = \frac{P(A \cap B)}{P(A)}$

Where P(B∣A) is the probability of event B given that A has occurred.

P(A∩B) is the probability of both events A and B occurring.

P(A) is the probability of event A occurring.

Probability when two events occurred simultaneously

The probability of two events occurring simultaneously has two cases, one is when the events are independent and the other one is when the events are dependent.

• For independent events: If events A and B are independent, the probability of both events occurring simultaneously is the product of the probability of the individual events, it is given by: P(A∩B) = P(A) × P(B)

• For dependent events: When events A and B are dependent, the probability of both events occurring simultaneously is given by: P(A∩B) = P(A) × P(B∣A), where P(B∣A) is the conditional probability of event B given that event A has already occurred.

Steps to Calculate Probability

• Define the Experiment: Determine the process or action that generates outcomes.

• Identify the Sample Space: List all possible outcomes of the experiment.

• Determine the Favorable Outcomes: Identify which of these outcomes meet the criteria of the event of interest.

• Apply the Probability Formula: Use the formula to calculate the probability of the event.

Example: What is the probability of getting a number greater than 4 when rolling a dice?

The experiment is rolling a single die.

The sample space S consists of all possible outcomes: S={1,2,3,4,5,6}

The favourable outcomes are {5,6}.

The required probability = $\frac{2}{6}$ = $\frac{1}{3}$.

What is a probability tree?

A probability tree is a diagram that represents all possible outcomes of an event and their probabilities. It is useful for calculating the probabilities of combined events.

Let us see a probability tree of tossing a coin twice to have a clear understanding of this.

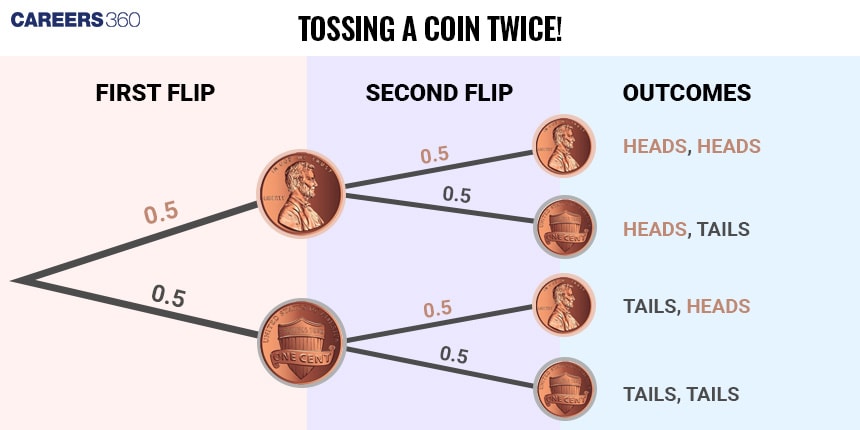
Types of Probability

• Classical Probability: Classical probability is based on the assumption that all outcomes of a random experiment are equally likely. It is calculated as the ratio of the number of favourable outcomes to the total number of possible outcomes. For example, the probability of rolling a 3 on a fair six-sided die is $\frac{1}{6}$.

• Empirical Probability: Empirical probability is based on observed data rather than theoretical calculations. It is determined by conducting experiments or collecting data and then calculating the probability based on the relative frequency of an event occurring in the data. For example, if a coin is flipped 100 times and lands on heads 55 times, the empirical probability of landing on heads is $\frac{55}{100}$ = 0.55.

• Subjective Probability: Subjective probability is based on personal judgment, intuition, or experience rather than objective data or mathematical calculation. It reflects an individual's belief about the likelihood of an event occurring, which may vary from person to person. For example, someone might estimate a 70% chance of their favourite sports team winning a game based on their analysis and feelings about the team's performance.

• Axiomatic Probability: Axiomatic probability is a formal framework for probability theory based on a set of axioms or fundamental principles. It provides a rigorous foundation by defining probability functions and operations through axioms, such as the probability of the entire sample space being 1 and the additivity of mutually exclusive events.

Probability Theory

Probability theory is the branch of mathematics concerned with the analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events. It provides the theoretical foundation for statistics and is used in various fields to model uncertainty and predict outcomes.

Probability density Function

A probability density function (PDF) describes the likelihood of a continuous random variable taking on a particular value. The area under the curve of the PDF represents the probability.

Application of probability

Probability has a wide variety of applications in real life. Some of the common applications that we see in our everyday lives while checking the results of the following events:

• Choosing a card from the deck of cards

• Flipping a coin

• Throwing a dice in the air

• Pulling a red ball out of a bucket of red and white balls

• Winning a lucky draw

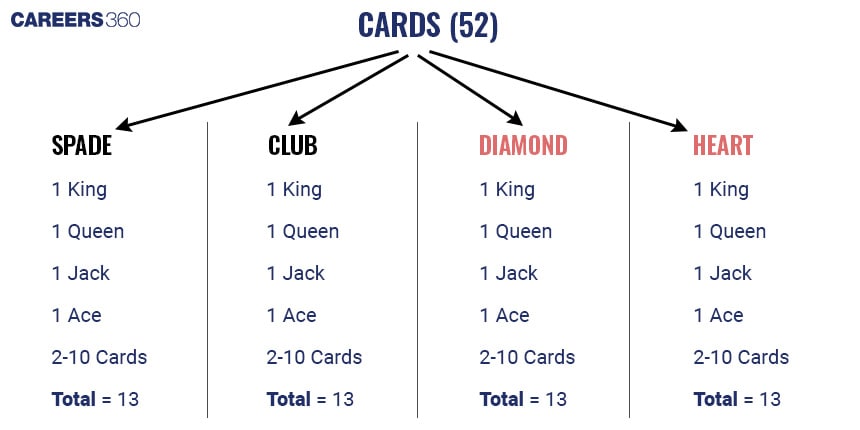
Understanding the deck of cards

A standard deck has 52 cards with 4 suits in two colors [hearts, diamonds, clubs, spades] each containing 13 ranks (2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace).

Tossing of a coin, Tossing of two or more coins

Each coin toss has 2 possible outcomes. Tossing two coins can result in HH, HT, TH, or TT.

Rolling a dice

A standard die has 6 faces numbered 1 to 6. Each face has an equal probability of $\frac{1}{6}$.

Theorems of Probability

Theorem 1: The sum of the probability of happening of an event and not happening of an event is equal to 1. P(A) + P(A') = 1.

Theorem 2: The probability of an impossible event or the probability of an event not happening is always equal to 0. P(ϕ) = 0.

Theorem 3: The probability of a sure event is always equal to 1. P(A) = 1

Theorem 4: The probability of happening of any event always lies between 0 and 1, i.e. 0 $\leq$ P(A) $\leq$ 1.

Theorem 5: If there are two events A and B, we can apply the formula of the union of two sets and we can derive the formula for the probability of happening of event A or event B as follows.

P(A∪B) = P(A) + P(B) - P(A∩B)

Also for two mutually exclusive events A and B, we have P( A U B) = P(A) + P(B)

Bays’ Theorem for Conditional Probability

Bayes’ Theorem provides a way to update the probability of an event based on new evidence. It is expressed as $P(A∣B) = \frac{P(B∣A). P(A)}{P(B)}$
where P(A∣B) is the probability of event A given that event B has occurred, P(B∣A) is the probability of observing B given A, P(A) is the prior probability of A, and P(B) is the total probability of B.

Law of Total Probability

The Law of Total Probability states that the probability of an event can be found by considering all possible ways that event can occur through a partition of the sample space. It is expressed as $P(B) = \sum_{i} P(B|A_i). P(A_i)$, where $A_i$ are mutually exclusive and exhaustive events that partition the sample space. This law allows us to compute P(B) by summing the probabilities of B occurring with each $A_i$ weighted by the probability of $A_i$.

Important Points

• The probability ranges from 0 to 1.

• The sum of probabilities of all possible outcomes in a sample space is 1.

• For mutually exclusive events, the probability of either event occurring is the sum of their individual probabilities.

Practice Questions / Solved Examples

Q.1.

A speaks the truth 5 out of 7 times and B speaks the truth 8 out of 9 times. What is the probability that they contradict each other in stating the same fact?

1. $\frac{1}{7}$

2. $\frac{1}{9}$

3. $\frac{1}{4}$

4. $\frac{1}{3}$

Hint: Required probability = (Probability of A speaking truth × Probability of B lying) + (Probability of A lying × Probability of B speaking truth)

Solution:

Probability of A speaking truth = $\frac{5}{7}$ = P(A)

⇒ Probability of A lying = $1-\frac{5}{7}$ = $\frac{2}{7}$ = P(A')

Probability of B speaking truth = $\frac{8}{9}$ = P(B)

⇒ Probability of B lying = $1-\frac{8}{9}$ = $\frac{1}{9}$ = P(B')

$\therefore$ Required probability

= P(A) × P(B′) + P(A′) × P(B)

= $\frac{5}{7}×\frac{1}{9}+\frac{2}{7}×\frac{8}{9}$

= $\frac{5}{63}+\frac{16}{63}$

= $\frac{21}{63}$

= $\frac{1}{3}$

Hence, the correct answer is $\frac{1}{3}$.

Q.2.

A glass jar contains 6 white, 8 black, 4 red, and 3 blue marbles. If a single marble is chosen at random from the jar, what is the probability that it is black or blue?

1. $\frac{8}{21}$

2. $\frac{11}{21}$

3. $\frac{5}{21}$

4. $\frac{1}{7}$

Hint: The probability of a chosen marble being black or blue = $\frac{\text{Total number of black and blue marbles}}{\text{total number of marbles}}$

Solution:

Given: A glass jar contains 6 white, 8 black, 4 red, and 3 blue marbles.

Number of total marbles = (6 + 8 + 4 + 3) = 21

Number of total black and blue marbles = (8 + 3) = 11

So, the probability of a chosen marble being black or blue = $\frac{11}{21}$

Hence, the correct answer is $\frac{11}{21}$.

Q.3.

The probabilities of solving a problem by three students A, B, and C are $\frac{3}{7}, \frac{5}{9}$ and $\frac{1}{5}$, respectively. The probability that the problem will be solved is:

1. $\frac{155}{315}$

2. $\frac{64}{315}$

3. $\frac{251}{315}$

4. $\frac{32}{315}$

Hint: If the probability in which someone solves a problem is $\frac{a}{b}$, then the probability in which he does not solve the problem is $\frac{b-a}{b}$.

Solution:

Let A, B, and C respectively denote the events that the problem is solved by A, B, and C respectively and A', B', and C' respectively denote the events that the problem will not be solved.

P(A) = $\frac{3}{7}$; P(A') = $\frac{4}{7}$

P(B) = $\frac{5}{9}$; P(B') = $\frac{4}{9}$

P(C) = $\frac{1}{5}$; P(C') = $\frac{4}{5}$

The problem will be solved if even one of them solves it.

So, first we calculate the probability that is not solved = P(A') × P(B') × P (C') = $\frac{4}{7}×\frac{4}{9}×\frac{4}{5}=\frac{64}{315}$

So, The required probability = $1-\frac{64}{315}=\frac{251}{315}$

Hence, the correct answer is $\frac{251}{315}$.

Q.4.

A person can hit a target 5 times out of 8 shots. If he fires 10 shots, what is the probability that he will hit the target twice?

1. $\frac{1135 \times 3^8}{8^{10}}$

2. $\frac{1165 \times 3^8}{8^{10}}$

3. $\frac{1175 \times 3^8}{8^{10}}$

4. $\frac{1125 \times 3^8}{8^{10}}$

Hint: First, find the probability of hitting and losing. Then find the required probability using them.

Solution:

Probability of hitting = $\frac{5}{8}$

Probability of losing = $\frac{3}{8}$

Probability of hitting twice when 10 shots are fired

= 10C2$(\frac{5}{8})^2(\frac{3}{8})^8$

= $\frac{10×9×5×5}{1×2}$× $\frac{ 3^8}{8^{10}}$

= $\frac{1125 ×3^8}{8^{10}}$

Hence, the correct answer is $\frac{1125 ×3^8}{8^{10}}$.

Q.5.

Draw a random card from a pack of cards. What is the probability that the card drawn is a face card?

1. $\frac{1}{13}$

2. $\frac{2}{13}$

3. $\frac{3}{14}$

4. $\frac{3}{13}$

Hint: The probability of an event A is,

P(A) = $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$
Solution:

A standard deck has 52 cards.

Total number of outcomes = n(S) = 52

Let E be the event of drawing a face card.

Number of favourable events = n(E) = 4 x 3 = 12 (considered Jack, Queen and King only)

Probability (P) = $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$

P(E) = $\frac{12}{52}$ = $\frac{3}{13}$

So, the probability of drawing a face card = $\frac{3}{13}$

Hence, the correct answer is $\frac{3}{13}$.

Q.6.

Two dice are rolled, find the probability that the sum is equal to 1.

1. 0

2. $\frac{1}{36}$

3. $\frac{5}{36}$

4. $\frac{7}{36}$

Hint: The probability of an event A is,

P(A) = $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$

Solution:

To find the probability that the sum is equal to 1 we have to first determine the sample space S of two dice.

Here n(S) = $6^2$ = 36

Since there are no outcomes where a sum is equal to 1,

So, the required probability = $\frac{0}{36}$ = 0

Hence, the correct answer is 0.

Q.7.

What is the probability of getting a sum of 10 when two dice are thrown?

1. $\frac{5}{12}$

2. $\frac{11}{12}$

3. $\frac{1}{12}$

4. $\frac{7}{12}$

Hint: The probability of an event A is,

P(A) = $\frac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$

Solution:

There are $6^2$ = 36 possibilities when we throw two dice.

The desired outcome is 10.

To get 10, we can have three favourable outcomes.

{(4,6),(6,4),(5,5)}

Number of favourable outcomes = 3

So, the probability of getting number 10 is $\frac{3}{36}$ = $\frac{1}{12}$

Hence, the correct answer is $\frac{1}{12}$.

FAQs

Q.1.

What is the formula of conditional Probability?

Answer:

$P(B∣A) = \frac{P(A \cap B)}{P(A)}$

Where P(B∣A) is the probability of event B given that A has occurred.

P(A∩B) is the probability of both events A and B occurring.

P(A) is the probability of event A occurring.

Q.2.

What is the probability of an impossible event?

Answer:

The probability of an impossible event is 0.

Q.3.

The probability of an event can be greater than 1. Is it true?

Answer:

No, the probability of an event ranges from 0 to 1.

Q.4.

What is the number of elements in the sample space of 3 coins?

Answer:

The sample space has $2^3$ = 8 elements.

Q.5.

What is the mathematical condition for impossible events?

Answer:

An event is impossible if its probability is 0.