Profit and Loss: Definition, Formula, Question, Examples

Profit and loss are part and parcel of our regular lives. It is also two essential terms in the field of Mathematics. We use the profit and loss formula to analyse financial outcomes in various transactions. In general, profit means gaining something and loss means losing something. Every product has a value like cost price and selling price. So, the profit and loss percentages decide if you gain or lose.

If a trader buys a cycle at a cost price of Rs. 1000 and sells it at Rs. 2000, then he has made a profit of Rs. 1000 as here cost price < selling price.

If the selling price was smaller, then he made a loss in that transaction.

In this article, we will discuss the profit and loss formula, profit and loss percentage formula, profit and loss statement format, profit and loss percentage formula in Excel, and some solved profit and loss questions.

Terminology used in Profit and Loss

To understand Profit and loss, we have to learn about the terminologies used in profit and loss. There are several key terminologies used in profit and loss like cost price, selling price, marked price, profit, loss, discount, and markup value.

Now we will access these terms thoroughly.

Cost Price

The total amount of money spent to produce a product including its additional expenses or the price a seller pays to acquire a product is called Cost price. It is generally denoted by CP.

Suppose to produce a cycle, the manufacturer spent Rs. 1500. So for that manufacturer Rs. 1500 is the cost price of that cycle.

The general formula of cost price:

Cost price = Selling price – Profit or, Cost price = Selling price + Loss

Selling Price

The amount a seller, trader or manufacturer generates from selling a product is called the selling price.

It is the price a buyer pays to buy the product. It is generally denoted by SP.

Suppose a manufacturer sells a cycle for Rs. 2000 to a buyer. Then for that manufacturer, Rs. 2000 will be the selling price. But for that buyer, it will be the cost price of that cycle. If he decides to sell the cycle in the future, then that will be his selling price.

The general formula of Selling price:

Selling price = Cost price + Profit or, Selling price = Cost price – Loss

Marked Price

To gain profit, sometimes a seller hikes the price of the products before giving any discounts. This price is called the Marked price.

It is generally denoted by MP.

The marked price is always greater than the cost price and greater or equal to the selling price.

Suppose the cost price of a shirt is Rs. 250. To gain a profit, the seller marks the tag price as Rs. 350.

So, here Rs. 350 is the marked price of that shirt.

The general formula of Marked price:

Marked price = Selling price + Discount

Profit

When the selling price is greater than the cost price or after giving a discount on the marked price, still the selling price is greater than the cost price, then we call it a Profit.

To have a profit, selling price > cost price

Suppose the cost price of a shirt is Rs. 200. If the selling price of that same shirt is Rs. 300, then we have made a profit.

The general formula is:

Profit = Selling price – Cost price

The formula to calculate Profit percentage is:

Profit percentage = $\frac{\text{Selling price – Cost price}}{\text{Cost price}}×100$

Loss

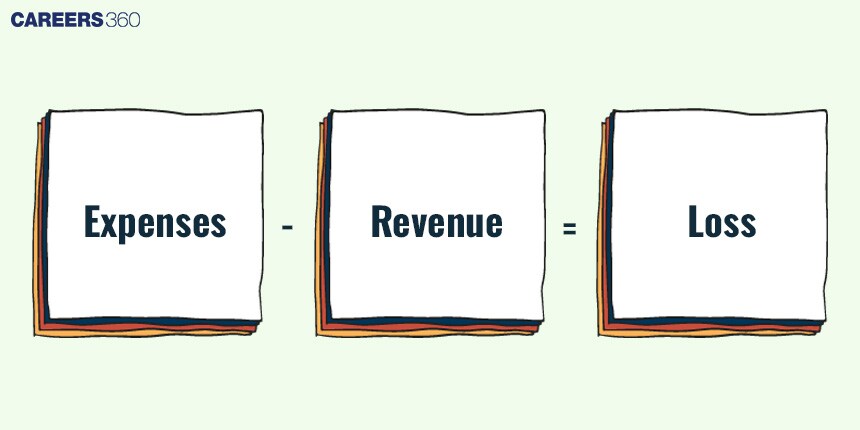
When the selling price is lower than the cost price or after giving a discount on the marked price, the selling price is lower than the cost price, so we call it a Loss.

To have a loss, selling price < cost price

Suppose the cost price of a shirt is Rs. 200. If the selling price of that same shirt is Rs. 150, then we have made a Loss.

The general formula is:

Loss = Cost price – Selling price

The formula to calculate the Loss percentage is:

Loss percentage = $\frac{\text{Cost price – Selling price}}{\text{Cost price}}×100$

Discount

The price gap between the marked price and the selling price is called the discount.

Suppose the marked price of a shirt is Rs. 300, and the selling price of that same shirt is Rs. 250, then the discount on that shirt is (Rs. 300 – Rs. 250) = Rs. 50

General formula of Discount is:

Discount = Marked price – Selling price

The formula to calculate the Discount percentage is:

Discount percentage = $\frac{\text{Marked price – Selling price}}{\text{Marked price}}×100$

Mark Up Value

Sellers or businessmen sometimes add a certain percentage to the cost price. This addition is called Percentage markup value. The price that becomes the markup is called the marked price.

It always depends on the cost price.

General formula of marked-up value is:

Marked-up value = Selling price/ Marked price – Cost price

Formulae used in Profit and Loss

How do we use the fractional equivalent of percentage to solve profit and loss problems?

The fractional equivalent of percentages can simplify calculations in profit and loss problems.

In the complex scenarios, it will help us to calculate faster.

We learned in percentages that to convert percentages into fractions, we have to divide it by 100.

We will get the decimal form of the value.

Let’s take an example to understand it better.

A trader buys an item for Rs. 200 and sells it for a profit of 20%.

We have to calculate the selling price.

First, we will convert the percentage into a fraction.

20% is equivalent to $\frac{1}{5}$, which means there is a profit of Rs. 1 on Rs. 5 and hence the selling price is Rs. 6

So, for the cost price of 200, the selling price = $\frac{6}{5} \times 200$ = Rs 240

Problems based on SP, CP, and MP

Understanding and solving problems based on Selling Price (SP), Cost Price (CP), and Marked Price (MP) is essential for grasping concepts of profit, loss, and discounts in business transactions.

Cost price or CP is the price at which an item is purchased.

The selling price or SP is the price at which an item is sold.

Marked price or MP is the initial price set by the seller before any discounts.

If CP and SP are given, and you have to calculate the profit percentage, then the formula is:

$\frac{\text{Selling price – Cost price}}{\text{Cost price}}×100$

Example:

Ten articles were bought for Rs. 8 and sold at 8 for Rs. 10. The gain percentage is:

Given:

The cost price of 10 books is Rs. 8.

The selling price of 8 books is Rs. 10.

Profit percentage = $\frac{\text{Selling price – Cost price}}{\text{Cost price}} × 100$

Let 40 books (LCM of 8 and 10) be bought.

Cost price of 40 books = Rs. $(\frac{8×40}{10})$ = Rs. 32

Their selling price = Rs. $(\frac{10×40}{8})$ = Rs. 50

The profit percentage = $(\frac{50-32}{32})$ × 100 = 56.25%

Hence, the gain percentage is 56.25%.

If CP and SP are given, and you have to calculate the loss percentage, then the formula is:

$\frac{\text{Cost price – Selling price}}{\text{Cost price}}×100$

Example:

What was the loss percentage if a computer with a cost price of Rs. 30,000 was sold for Rs. 28,000?

Given: The cost price is Rs. 30,000 and the selling price is Rs. 28,000.

Loss Percentage $=\frac{\text{(Cost price - Selling price)}}{\text{Cost price}}×100$

$\therefore$ Loss Percentage $=\frac{(30000–28000)}{30000}×100=\frac{20}{3} =6\frac{2}{3}\%$

Hence, the loss percentage is $6\frac{2}{3}\%$.

If MP and discount are given, then Marked price - Discount = Selling price

Example:

The cost price of an article is Rs. 5500. It was sold at a profit of 9.09%. If the article was sold at a discount of 20%, then what is the marked price (in Rs.) of the article?

The cost price of an article is Rs. 5500.

It was sold at a profit of 9.09%.

$\therefore$ Selling price $=\frac{100+9.09}{100}×5500 = 6000$

It was sold at a discount of 20%.

$\therefore$ Marked price $=\frac{100}{100-20}×6000=7500$

Hence, the marked price of the article is Rs. 7500.

Problems based on Successive discounts

Giving back-to-back discounts on Cost price or Marked price is called a successful discount.

To solve this type of problem, we have to convert successive discounts into a single equivalent discount.

Single equivalent discount = $(a+b-\frac{a×b}{100}$)%, where $a$% and $b$% are successive discounts.

Another way to solve this type of problem is by applying each discount sequentially to the price obtained after the previous discount.

Selling price = $\frac{100-\text{Discount}_1\%}{100}× \frac{100-\text{Discount}_2\%}{100}×$ Marked price/Cost price

When the CP of two articles is the same

Sometimes there will be two articles with the same cost price(CP) and different profit or loss percentages. To calculate the total profit or loss margin during those transactions, we have to calculate separately the selling prices and add them together.

Example:

Kushal purchased two sets of jeans for INR 4,000 each. He sold these sets of jeans, gaining 8% on one and losing 6% on the other.

We have to calculate his total loss or gain in this whole transaction.

We know, Selling price = $\frac{100+ \text{Profit}\%}{100}×$ Cost price

So, selling price of 1st set of jeans is $\frac{108}{100}×4000$ = INR 4320

Also, Selling price = $\frac{100- \text{Loss}\%}{100}×$ Cost price

So, selling price of 2nd set of jeans is $\frac{94}{100}×4000$ = INR 3760

Total selling price = (4320 + 3760) = INR 8080

$\therefore$ His profit is (8080 – 8000) = INR 80

Hence, Kushal has a gain of INR 80.

When the SP of two articles is the same

When the selling price (SP) of two articles is the same and different profit or loss percentages, then we have to calculate the cost price separately and add them together to get the overall profit or loss margin in this type of transaction.

If Selling prices are the same and the profit-loss percentages are the same, then in such transactions, there is always a loss.

Then, the formula to find the loss percentage

Loss percentage = $\frac{x^2}{100}$%

where x is profit% and loss%.

Example:

A refrigerator and a washing machine were sold for Rs. 24000 each. If the refrigerator was sold at a gain of 20% and the washing machine at a loss of 20%.

We have to calculate the overall loss or gain in this whole transaction.

Solution:

Loss % = $\frac{20^2}{100}$ = 4% loss

If the cost price is 100, then the loss will be 4, and the selling price is 96. It means loss is $\frac{1}{24}$ of the total selling price.
So, Loss = $\frac{48000}{24}$ = Rs 2000.

Dishonest Shopkeeper and Faulty Weight

Sometimes dishonest shopkeepers use faulty weight to earn more profit and give buyers a lesser quantity of items.

In these cases, to calculate the profit percentage, the formula is:

$\frac{\text{Faulty weight – True weight}}{\text{True weight}}×100$

Example:

A shopkeeper weighs an item of 930 grams instead of 1 kg and sells it at its cost price. Find his profit percentage on selling 15 kg of the item.

Here,

Faulty weight = 930 gm

True weight = 1000 gm

Gain Percentage = $\frac{\text{Error}}{\text{True Value - Error}}×100$

Error = 1000 – 930 = 70 gm

The profit percentage on buying 15 kg will be the same as buying 1 kg.

Gain Percentage = $\frac{70}{1000-70} \times 100$

⇒ Gain % = $\frac{70}{930} \times 100 = 7\frac{49}{93}$%

Hence, his profit is $ 7\frac{49}{93}$%.

Miscellaneous

1. After giving a discount of 20% on an article, a shopkeeper gains 20%. What is the percentage markup?

Let the cost price of the article be 100.

Here, the profit is 20%.

So, the selling price of the article = 120

Let the marked price of the article be $x$.

According to the question,

80% of $x$ = 120

⇒ $x$ = 150

So, the percentage mark-up $=\frac {150 – 100}{100} = 50$%

Hence, the correct answer is 50%.

2. The selling and the cost price of an article are Rs. 3960 and Rs. 3600, respectively. If a 12% discount was given, what is the percentage mark-up?

Given: The cost price is Rs. 3600 and the selling price is Rs. 3960.

Let the marked price be Rs. $x$.

$\text{SP}=\text{MP}-\frac{\text{Discount%}}{100}×\text{MP}$, where MP = marked price, CP = cost price

$⇒ 3960=x-\frac{12}{100}×x$

$⇒ 3960=\frac{88x}{100}$

$⇒ x = 4500$

So, the article's cost is Rs. 3600.

Now, percentage mark-up = $\frac{\text{MP-CP}}{\text{CP}}\times100$

So, the percentage mark-up $=\frac{4500–3600}{3600}\times100=25$%

Hence, the correct answer is 25%.

Tips and Tricks

• If Selling prices are the same and the profit-loss percentages are the same, then in such transactions, there is always a loss.

Loss percentage in those transactions = $\frac{\text{Loss}^2}{100}$

• Single equivalent discount = $(a+b-\frac{a×b}{100}$)%, where $a$% and $b$% are successive discounts.

• When there is one profit of a% and a loss of b%, then the net profit or loss percentage is

$(a-b-\frac{a×b}{100}$)%

• To calculate the profit percentage for dishonest sellers, the formula is:

$\frac{\text{Faulty weight – True weight}}{\text{True weight}}×100$

Solved Examples

Q1. If the selling price of 40 articles is equal to the cost price of 50 articles, the loss or gain percent is:

1. 25% gain

2. 20% gain

3. 25% loss

4. 20% loss

Hint: Use this formula: Profit % = $\frac{\text {Profit}}{\text {Cost price}}\times 100$

Answer:

Let the cost price of each article be Re. 1.

Selling price (SP) of 40 articles = cost price (CP) of 50 articles = Rs. 50

CP of 40 articles = Rs. 40

Profit on 40 articles = SP of 40 articles – CP of 40 articles = 50 – 40 = 10

Profit % =$\frac{\text {Profit}}{\text {Cost price}}\times 100 =\frac {10}{40}\times 100=25\%$

Hence, the correct answer is 25% gain.

Q2. A horse was sold for Rs. 60,000 at a profit of 20%. For what price should he have sold to gain a 30% profit?

1. Rs. 64,000

2. Rs. 65,000

3. Rs. 50,000

4. Rs. 55,000

Hint: Cost price $=\frac{100}{\text{100 + Profit %}}×$ Selling price

Answer:

Selling price of the horse at a profit of 20% = Rs. 60,000

$\therefore$ Cost price of the horse $=\frac{100}{100+20}×60000=50000$

To get a profit of 30%, new selling price of the horse $=\frac{100+30}{100}×50000=65000$

Hence, the correct answer is Rs. 65,000.

Q3. If a vendor sells a coconut for Rs. 14.4, he makes a 10% loss. If he wants to make a 25% profit, then at what price (in Rs.) should he sell?

1. 18

2. 20

3. 16

4. 22

Hint: Find cost price by: Cost price = $\frac{\text{Selling price×100}}{100-Loss\%}$

Find selling price by: Selling price = $\frac{\text{Cost price (100+Profit%)}}{100}$

Answer:

Given: The Selling price of a coconut = Rs. 14.4

Loss percent = 10%

Cost price = $\frac{\text{Selling price×100}}{100-Loss\%}$

Cost price = $\frac{14.4}{0.9}=16$

Selling price = $\frac{\text{Cost price (100+Profit%)}}{100}$

For 25% profit, Selling price = $16\times 1.25$ = Rs. 20

Hence, the correct answer is Rs. 20.

Q4. If two successive discounts of 50% and 10% are offered, what is the net discount (in %)?

1. 50

2. 55

3. 60

4. 65

Hint: Single equivalent discount = $(a+b-\frac{a×b}{100}$)%, where $a$% and $b$% are successive discounts.

Answer:

Single equivalent discount = $(a+b-\frac{a×b}{100}$)%, where $a$% and $b$% are successive discounts.

First discount = 50%

Second discount = 10%

So, single discount = $50 + 10 - \frac{50×10}{100}= 55$%

Hence, the correct answer is 55.

Q5. When a discount of Rs. 42 is allowed on the Marked price of an article, the new reduced price becomes 86% of the original price. Find the Marked price.

1. Rs. 250

2. Rs. 300

3. Rs. 350

4. Rs. 400

Hint: Use the concept, Discount = Marked price – Selling price

Answer:

Let the original Marked price be Rs. 100.

So, the discount is = (100 – 86) = Rs. 14

Now for the discount of Rs. 14, the original Marked price is = Rs. 100

Then for the discount of Rs .42, the original Marked price is = $(\frac{100×42}{14})$ = Rs. 300

Hence, the correct answer is Rs. 300.

Q6. A sells a car priced at Rs. 36000. He gives a discount of 8% on the first Rs. 20,000 and 5% on the remaining Rs. 16,000. B also sells a car of the same make, priced at Rs. 36000. He gives a discount of 7% on the total price. Calculate the actual prices charged by A and B for the cars.

1. A = Rs. 33,500, B = Rs. 33,400

2. A = Rs. 33,480, B = Rs. 33,600

3. A = Rs. 33,450, B = Rs. 33,650

4. A = Rs. 33,600, B = Rs. 33,480

Hint: Selling price = $\frac{100- \text{Discount}\%}{100}×$ cost price

Answer:

Selling price of A = Rs. 36000

Total discount by A = $20000 \times \frac{8}{100}+16000 \times \frac{5}{100}$ = 1600 + 800 = Rs. 2400

$\therefore$ Actual price charged by A = Rs. 36000 − Rs. 2400 = Rs. 33600

Actual price charged by B = Rs. $36000\times \frac{100−7}{100}= 36000\times \frac{93}{100}$ = Rs. 33480

Hence, the correct answer is A = Rs. 33600 and B = Rs. 33480.

Q7. The marked price of an article is 50% more than its cost price. If a 20% discount is given, then what will be the profit percentage?

1. 20%

2. 25%

3. 30%

4. 50%

Hint: Assume the cost price is 100 units, then calculate the marked price.

Answer:

Given: The marked price of an article is 50% more than its cost price.

Let the cost price be 100 units.

So, the marked price is 100 + 50 = 150

20% discount is given,

So, selling price is $\frac{100-20}{100}×150=120$

$\therefore$ Profit = (Selling Price – Cost Price) = 120 – 100 = 20

So, the profit percentage is 20%.

Hence, the correct answer is 20%.

Q8. A shopkeeper used to allow a discount of Rs. 20 on a product. He doubled the discount on the product and sold it for Rs. 80. What was the percentage of the discount offered?

1. 20%

2. 25%

3. 30%

4. 33.33%

Hint: First, find the marked price of the article and then use this information to solve the question.

Answer:

New discount = Rs. 40

Selling price = Rs. 80

Marked Price of the article = Rs. 80 + Rs. 40 = Rs. 120

If the discount is $x$%, then,

$x$% of 120 = 40

⇒ $\frac{x}{100} \times 120 = 40$

⇒ $x = \frac{40 \times 100}{120}$

$\therefore x = 33.33$%

Hence, the correct answer is 33.33%.

Q9. Ramesh marks his goods 30% above the cost price. If he sells the item for Rs. 910 after allowing a discount of 15%, find his cost price.

1. Rs. 823.5

2. Rs. 758

3. Rs. 814.2

4. Rs. 856.5

Hint: Selling price = $\frac{100-\text{Discount}\%}{100}×\text{Marked price}$

Answer:

Let the cost price of the article be $x$.

Ramesh marks his goods 30% above cost price = $x \times \frac{130}{100} = \frac{13x}{10}$

Now, according to the question:

The item is sold at a 15% discount.

⇒ $\frac{13x}{10} \times \frac{85}{100} = 910$

$\therefore x= \frac{910000}{1105} = 823.5$

Hence, the correct answer is Rs. 823.5.

Q10. The difference between a discount of 30% on Rs. 2,000 and two successive discounts of 25% and 5% on the same amount is:

1. Rs. 30

2. Rs. 35

3. Rs. 25

4. Rs. 40

Hint: For two successive discounts Selling Price = $\frac{100-\text{Discount}_1\%}{100}× \frac{100-\text{Discount}_2\%}{100}×$ Marked Price

Answer:

Amount = Rs. 2,000

If discount = 30%, final amount = $\frac{70}{100}$ × 2000 = Rs. 1,400

If two successive discounts of 25% and 5%,

final amount = $\frac{75}{100}$ × $\frac{95}{100}$ × 2000 = Rs. 1,425

$\therefore$ Difference = 1425 – 1400 = Rs. 25

Hence, the correct answer is Rs. 25.

Q11. A double bed is marked at Rs. 7,500. The shopkeeper allows successive discounts of 8%, 5%, and 2% on it. What is the net selling price?

1. Rs. 6,500

2. Rs. 6,000

3. Rs. 6423.90

4. Rs. 6500.50

Hint: Use the successive discount formula of $a$% and $b\%$, which is equivalent to $(a+b-\frac{a×b}{100}$)%.

Answer:

We know,

$\text{Single discount}=(a+b-\frac{a×b}{100}$)%

Where $a,b$ are successive discounts.

$\therefore$ Single equivalent discount of two successive discounts of 8% and 5% $=8+5- \frac{8×5}{100}=13-0.4=12.6$%

Now, the single equivalent discount of two successive discounts of 12.6% and 2% $=12.6+2-\frac{12.6×2}{100}=14.6-0.252=14.348$%

The double bed is marked at Rs. 7500.

So, Selling price $=7500×\frac{100-14.348}{100}=7500×\frac{85.652}{100}$ = Rs. $6423.90$

Hence, the correct answer is Rs. 6,423.90.

Q12. A merchant changed his trade discount from 25% to 15%. This would increase his selling price by:

1. $3\frac{1}{3}$%

2. $6\frac{1}{6}$%

3. $13\frac{1}{3}$%

4. $16\frac{1}{3}$%

Hint: Use the formula: $\text{Price Increase} = \frac{\text{Total Increase}}{\text{Original Price}}×100$

Answer:

Given: A merchant changed his trade discount from 25% to 15%.

Let the marked price be Rs. 100.

Now for a 25% discount the selling price is = (100 – 25) = Rs. 75

and for a 15% discount, the selling price is = (100 – 15) = Rs. 85

So, the increase in the selling price

= ($\frac{85-75}{75}$×100)

= $\frac{40}{3}$

= $13\frac{1}{3}$%

Hence, the correct answer is $13\frac{1}{3}$%.

Q13. When a discount of 25% is given on a cruise trip, the profit is 41%. If the discount is 26%, then the profit is:

1. 39.12%

2. 67%

3. 94.88%

4. 11.24%

Hint: The selling price is the sum of cost price and profit. The marked price is the sum of the selling price and the discount.

Answer:

Let the cost price be Rs. 100.

When profit % = 41, selling price = 100 + 41 = Rs. 141

When discount = 25%, selling price = 75% of Marked price

Marked price = $\frac{141}{\frac{75}{100}}$ = $\frac{141}{\frac{3}{4}}$ = $\frac{141 × 4}{3}$ = Rs. 188

When discount = 26%, Selling price = 74% of marked price

Selling price = 74% of Rs. 188 = $\frac{188 × 74}{100}$ = Rs. 139.12

Profit = Rs. 139.12 – Rs. 100 = Rs. 39.12

Profit percentage = $\frac{39.12 × 100}{100}$ = 39.12%

Hence, the correct answer is 39.12%.

Q14. A dishonest shopkeeper sells millet at 20 per kg, which he has bought at 16 per kg, and he is giving 800 gm instead of 1000 gm. Find his actual profit percentage.

1. 52.12%

2. 58.36%

3. 54.25%

4. 56.25%

Hint: Find the actual cost price by calculating the actual amount of millet sold.

Answer:

Here, CP = Cost price, SP = Selling price

CP of 1000 gm of millet = Rs. 16

CP of 1 gm of millet = $\frac{16}{1000}$ = Rs. 0.016

He gave only 800 gm.

CP of 800 gm of millet = $0.016 \times 800$ = Rs. $12.8$

SP of 800 gm of millet = Rs. 20

Profit = 20 – 12.8 = Rs. 7.2

Profit percent $=\frac{7.2}{12.8}\times 100 = 56.25\%$

Hence, the correct answer is 56.25%.

Q15. A shopkeeper sells rice at 10% profit and uses a weight that is 30% less than the actual measure. His gain percentage is:

1. $57\frac{1}{8}\%$

2. $57\frac{1}{7}\%$

3. $57\frac{2}{5}\%$

4. $57\frac{3}{7}\%$

Hint: First, assume the cost price (CP) of 1 kg of rice is Rs. 100. Then, find the selling price (SP) of 700 gm and 1000 gm of rice. Use this formula:

Profit percentage = $\frac{\text{Profit}}{\text{CP}}×100$

Answer:

Let the cost price (CP) of 1 kg. of rice be Rs. 100.

As he uses 30% less weight and sells at 10% profit,

Selling price (SP) of (1000 – 300) = 700 gm of rice = Rs. 110

⇒ SP of 1000 gm of rice = $\frac{110}{700}×1000$ = $\frac{1100}{7}$

So, profit = SP – CP = $\frac{1100}{7}-100$ = $\frac{400}{7}$

Profit Percentage = $\frac{\text{Profit}}{\text{CP}}×100$ = $\frac{\frac{400}{7}}{100}×100$ = $\frac{400}{7}$ = $57\frac{1}{7}\%$

Hence, the correct answer is $57\frac{1}{7}\%$.